Параметры электрических аппаратов

Примеры решения задач по электрическим аппаратам

 

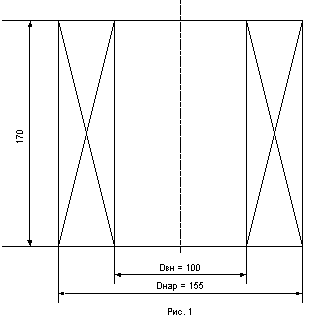
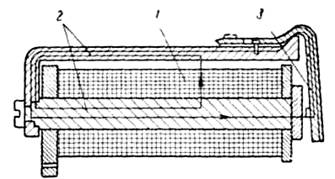
1. Определить длительно допустимую величину плотности переменного тока для бескаркасной цилиндрической катушки индуктивности, намотанной медным проводом диаметром d = 4мм. Изоляция провода хлопчатобумажная без пропитки, число витков катушки w = 250, остальные необходимые размеры даны на рис. 1. Катушка находиться в спокойном воздухе.

 

Решение: Исходя из закона Джоуля-Ленса потери энергии, выделяющейся в катушке,

В длительном режиме работы вся выделенная энергия в катушке должна быть отведена в окружающую среду. Мощность, отводимая в окружающую среду, , где С – температура окружающей среды; в качестве ϑ берем величину допустимой температуры для данного класса изоляции ϑ_доп = 90 ^оС.

Коэффициент теплоотдачи

.

Поскольку должно быть равенство между выделенной в катушке и отводимой с ее поверхности тепловыми мощностями, то исходным уравнением для нахождения допустимой плотности тока будет:

,

Откуда

,

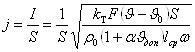где,  – площадь поперечного сечения провода; r₀ = 1,62 ∙ 10^-6 Ом ∙ см; a = 0,0043 1/град; ;

 – длина среднего витка катушки. Тогда

,

а плотность переменного тока

 

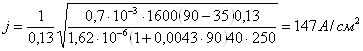
Ответ: j = 1,5 А/мм

2. Написать уравнение кривой нагрева круглого медного проводника диаметром d = 10 мм, по которому протекает постоянный ток I = 400 А. Известно, что средний коэффициент теплоотдачи с поверхности проводника k_T = 10 Вт/(м²∙град), температура окружающей среды, которой является спокойный воздух, ϑ₀ = 35°С, а средняя величина удельного сопротивления меди за время нарастания температуры r = 1,75-10^-8 Ом∙м

Решение: Уравнение кривой нагрева в простейшем случае имеет вид

где θ_уст = P/(k_xF) — установившееся превышение температуры. Расчет θ_уст и Т произведем на единице длины проводника l = 1 м, поэтому

Постоянная времени нагрева

,

где с — удельная теплоемкость меди; М = γ V— масса стержня длиной в 1 м; γ — плотность меди; V — объем проводника; F — охлаждающая поверхность.

Таким образом, уравнение кривой нагрева θ = 113 (1 – e^-t/850)

Ответ: θ = 113 (1 – e^-t/850)

3. Определить, какое количество тепла передается излучением в установившемся режиме теплообмена от нагретой шины к холодной, если шины размером 120 х 10 мм² расположены параллельно друг другу на расстоянии S = 20 мм. Шина, по которой протекает переменный ток, нагревается до температуры ϑ₁ = 120 °С. Температура другой шины ϑ₁ = 35 °С. Обе шины медные и окрашены масляной краской

Решение: Количество тепла, передающееся излучением от нагретой шины к холодной,

Рассчитаем теплообмен на длине шин l = 1м. Учитывая, что F₁φ₁₂= F₂φ₂₁, имеем

,

где F₁ – теплоотдающая поверхность нагретой шины.

Коэффициент

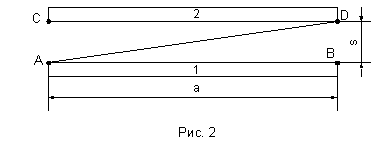
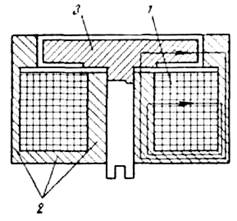
Обозначения показаны на рис. 2: ; F_BC’C = F_BC = F_AD;

Поскольку F₁ = F₂ = 120 ∙ 10^-3 м², то φ₂₁ = φ₁₂ = 0,82.

Тогда

 

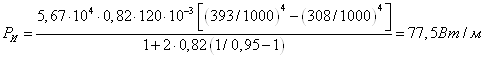
Ответ: Р_И = 77,5 Вт/м

 

4. Определить установившееся значение температуры медного круглого стержня диаметром d = 10 мм на расстоянии 0,5 м от его торца, который находится в расплавленном олове, имеющем температуру ϑ_mах = 250°С. Стержень находится в воздухе с ϑ₀ = 35°С, при этом коэффициент теплоотдачи с его поверхности k_т = 25 Вт/(м²·град). Определить также тепловой поток, который отводится с боковой поверхности стержня длиной 0,5 м, считая от поверхности олова

 

Решение: Из формулы

 

где

Здесь λ = 390 Вт/(м·град) — коэффициент теплопроводности меди, температура стержня ϑ = 50,6°С.

Величина теплового потока с боковой поверхности стержня

 

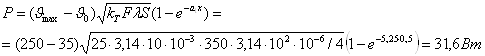
Ответ: ϑ = 50,6°С; Р = 31,6 Вт.

5. Определить электродинамическое усилие, действующее на 10 м прямолинейного бесконечного тонкого уединенного проводника с током к.з. I = 50 кА. Проводник находится в поле земли и расположен под углом γ = 30° к плоскости магнитного меридиана. Горизонтальная составляющая напряженности магнитного поля Н = 12,7 А/м а угол наклонения β = 72°

 

Решение: Действующие на проводник усилия

,

где ; Г/м.

Тогда горизонтальная составляющая индукции земного поля:

 

 Т;

Вертикальная составляющая:

Т.

Определим две составляющие силы, действующие на проводник:

от горизонтальной составляющей вектора индукции

Н

и от вертикальной

Н.

Суммарное усилие, действующее на проводник,

Н.

 

Ответ: F = 24,9H.

6. Определить усилия, действующие на каждый из ножей терхполюсного разъединителя, по которому протекает предельный сквозной ток трехфазного К.З. Амплитудное значение тока I_max=320 кA, длина ножей l = 610 мм, расстояние меду ними h = 700 мм. Вычислить также требуемый момент сопротивления поперечного сечения ножей

Решение: В случае установившегося тока К.З. будут действовать знакопеременные времени усилия. Определим максимальные притягивающие и максимальные отталкивающие усилия на каждый из трех ножей разъединителя (рис. 3):

 

 

где

 

 

Наиболее напряженным будет средний полюс, поэтому его необходимо рассчитывать на прочность изгиба как балку на двух опорах. Требуемое значение момента сопротивления поперечного сечения

где  – изгибающий момент;

Па – допустимое напряжение на изгиб для ножей, выполненных из меди

0твет:

7. Определить величину электродинамического усилия, действующего на 1 м круглого проводника диаметром d = 20 мм. Проводник расположен на расстоянии а/2 = 10 см вдоль ферромагнитной стенки и по нему протекает ток I = 1000 А

Решение: Поскольку диаметр проводника значительно меньше, чем расстояние до ферромагнитной стенки, то к решению следует подходить, как и в случае бесконечно тонкого проводника. Методом зеркального изображения найдем электродинамическое усилие, которое действует между данным проводником и его зеркальным изображением относительно поверхности ферромагнитной стенки с тем же током I.

Тогда

где ;

Ответ: F = 1.0 Н.

8. Определить скорость движения открытой (свободной) дуги с током I_д = 400 А, находящейся в поперечном магнитном поле с индукцией B = 0,05 T

 

Решение: Для индукции в пределах 0 < B < 0,1 T, по формуле Кукекова,

где ,

Ответ:

 

9. Определить энергию, поглощенную дугой постоянного тока при ее гашении, если сопротивление отключаемой цепи R = 1 Ом, индуктивность цепи L = 100 мГ, спад тока имеет прямолинейный тхарактер (рис. 4), время угасания дуги t_д = 0,1 с, напряжение цепи U_n = 200 В

Решение: Исходя из уравнения напряжений:

,

получаем выражение энергии дуги

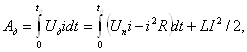
где— ток цепи.

Интеграл в правой части уравнения представляет собой энергию, поглощенную в дуге и подведенную за время гашения от источника за время гашения дуги t_д= 0,1 с. Интеграл может быть вычислен, если задана зависимость изменении тока во времени. По условию задачи, ток в зависимости от времени падает по прямой и тогда величина общей поглощенной энергии

 

Ответ: А_д = 2670Дж.

Примечание. Из примера видно, что основная доля энергии, поглощенная дугой, определяется энергией, запасенной в индуктивности. Такие соотношения обычно возникают при больших индуктивностях цепи и малом времени горения дуги.

10. Определить полное время горения дуги, если напряжение на дуге U_д = 250В в зависимости от тока остается постоянным. Напряжение сети U_и = 200В, сопротивление R = 1 Ом, индуктивность L = 15 мГ

 

Решение: полное время горения дуги

 

Значение  Подставив ∆U в выражение для t_д и проинтегрировав его, получим:

Ответ: