Навигация
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ.
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА М.Ф. РЕШЕТНЕВА.
Кафедра физики.
Реферат
по дисциплине "Физика"
На тему:
«Понятие сплошной среды. Уравнение движения сплошной среды. Модели сплошной среды – идеальная и вязкая жидкости. Уравнение Навье-Стокса. Силы, действующие в атмосфере. Уравнение движения свободной атмосферы. Геострофический ветер. Градиентный ветер. Циркуляция атмосферы. Образование волновых движений в атмосфере»
Выполнил: студент 2-го курса
группы ИУТ-61
Нечаев М. С.
Проверил:
Баринов Г. И.
Красноярск 2007
Содержание
1. Понятие сплошной среды.. 3
2. Уравнение движения сплошной среды.. 3
3. Модели сплошной среды.. 4
3.1. Уравнение Навье-Стокса. 5
4. Силы, действующие в атмосфере. 5
5. Уравнение движения свободной атмосферы.. 6
6. Геострофический ветер. 7
7. Градиентный ветер. 8
8. Циркуляция атмосферы.. 9
9. Образование волновых движений в атмосфере. 12
Список использованной литературы.. 14
1. Понятие сплошной среды
Механика сплошной среды, раздел механики, посвященный изучению движения и равновесия газов, жидкостей и деформируемых твёрдых тел. К Механика сплошной среды относятся: гидроаэромеханика, газовая динамика, упругости теория, пластичности теория и др. Основное допущение Механика сплошной среды состоит в том, что вещество можно рассматривать как непрерывную, сплошную среду, пренебрегая его молекулярным (атомным) строением, и одновременно считать непрерывным распределение в среде всех её характеристик (плотности, напряжений, скоростей частиц и др.). Это оправдывается тем, что размеры молекул ничтожно малы по сравнению с размерами частиц, которые рассматриваются при теоретических и экспериментальных исследованиях в Механика сплошной среды Поэтому можно применить в Механика сплошной среды хорошо разработанный для непрерывных функций аппарат высшей математики.
Исходными в Механика сплошной среды при изучении любой среды являются: 1) уравнения движения или равновесия среды, получаемые как следствие основных законов механики, 2) уравнение неразрывности (сплошности) среды, являющееся следствием закона сохранения массы, 3) уравнение энергии. Особенности каждой конкретной среды учитываются т. н. уравнением состояния или реологическим уравнением, устанавливающим для данной среды вид зависимости между напряжениями или скоростями изменения напряжений и деформациями или скоростями деформаций частиц. Характеристики среды могут также зависеть от температуры и др. физико-химических параметров; вид таких зависимостей должен устанавливаться дополнительно. Кроме того, при решении каждой конкретной задачи должны задаваться начальные и граничные условия, вид которых тоже зависит от особенностей среды.
Механика сплошной среды находит огромное число важных приложений в различных областях физики и техники.
2. Уравнение движения сплошной среды
Основное дифференциальное уравнение движения сплошной среды:
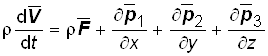, (2.4)
или в проекциях на оси декартовой системы координат:
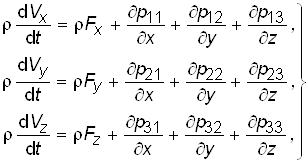(2.5)
где 
– компоненты массовой силы 
.
Отметим, что уравнения (2.4) и (2.5) получены при следующих предположениях:
– непрерывность и дифференцируемость векторов напряжений 
1, 2, 3,
– неразрывность среды,
– непрерывность характеристик движения.
3. Модели сплошной среды
Экспериментальные данные показывают, что большинство сред обладает специфическим свойством: отсутствием или малостью касательных напряжений pSt, т.е. вектор S можно считать перпендикулярным любой площадке взаимодействия dS и равным нормальному напряжению pSn. Среду, обладающую таким свойством называют идеальной жидкостью или идеальным газом. Близки к таковым обычные воздух и вода при малых скоростях.
Указанное свойство для любой площадки с нормалью 
можно выразить соотношением, вытекающим из (2.1):
,
где –p – общее значение скалярных произведений. Величину p называют давлением. Его особенность заключается в независимости от направления рассматриваемого взаимодействия частиц. При p > 0 среда, как показывает опыт, находится в сжатом состоянии, поэтому и использован знак минус. Таким образом, матрица компонент тензора внутренних напряжений в идеальной жидкости (газе) имеет вид:
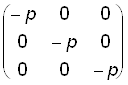, (2.6)
и тензор P целиком определяется скаляром p.
Понятно, что идеальная жидкость не единственно возможная модель сплошной среды, позволяющая определить компоненты тензора внутренних напряжений. Можно, например, рассматривать его компоненты как функции от деформации частицы: в этом случае среда называется упругой. В частном случае линейности это соотношение приобретает вид закона Гука. Изучением таких сред занимается теория упругости.
Особое место в механике сплошной среды занимает модель вязкой жидкости, предполагающая связь тензора внутренних напряжений с частными производными скорости по координатам. Имеется в виду эффект "трения" слоев вязкой жидкости между собой при наличии разности их поступательных скоростей.
Похожие работы
... Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4). В случае стационарных электрических и магнитных полей ( и) система уравнений Максвелла (1) – (4) распадается на систему уравнений электростатики: , , ...
... характере деформирования Расчет конструкций и их элементов с учетом всего многообразия физико-механических свойств реальных материалов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому, отказываясь от принятой в теоретической механике модели абсолютно твердого тела, в сопротивлении материалов приходится вводить свою модель — модель идеализированного ...
праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...
... заранее подготовленные учащимися доклады и рефераты по теме. Изложение темы можно завершить демонстрацией фильма «Плазма – четвёртое состояние вещества». 3. Перспективы в области изучение плазмы в школьном курсе. Возможные пути для изучения плазмы. Как я уже упоминал ранее, объём преподаваемого материала по теме «Плазма» крайне мал, даже по сравнению с тем же материалом за границей. ...
0 комментариев