Навигация
3.1. Уравнение Навье-Стокса
В частном случае линейности связь представляется в виде закона Навье-Стокса (или обобщенного закона вязкости Ньютона):
, (2.7)
где 
– элементы единичной матрицы (с единицами на главной диагонали и нулями на всех остальных местах), матрица размерности 3´3, обозначенная emn, называется тензором скоростей деформации, а тензорный коэффициент линейности Bijmn описывает свойства вязкой жидкости.
Если свойства среды в разных направлениях одинаковы, то она называется изотропной, в противном случае – анизотропной. В изотропной среде Bijmn представляется симметричной матрицей размерности 3´3´3´3, одинаковой в любой системе координат. Можно показать [1], что в этом случае все компоненты тензора Bijmn выражаются всего лишь через два независимых параметра l и m, называемых коэффициентами Ламе, поэтому закон Навье-Стокса для вязкой изотропной жидкости имеет вид:
. (2.8)
4. Силы, действующие в атмосфере.
Силы, действующие в атмосфере делятся на массовые и поверхностные:
Массовые или объемные силы.
К массовым силам относятся те силы, которые действуют на каждый элементарный объем воздуха, и обычно, рассчитываются на единицу массы. К ним относятся:
Сила тяжести 
представляет собой векторную сумму двух сил: силы земного притяжения, направленной к центру Земли, и центробежной силы, возникающая из-за вращения Земли вокруг своей оси и направленная по радиусу круга широты, проходящей через рассматриваемую точку.
Сила Кориолиса (отклоняющая сила вращения земли) 
связана с вращением Земли вокруг своей оси и действует на движущиеся относительно Земли частицы воздуха (на воздушные течения атмосферы). Сила Кориолиса возникает в результате переносного вращательного движения Земли и одновременного движения частиц воздуха относительно земной поверхности.
или 
.
где ω – угловая скорость вращения Земли.
Применяя формулы векторного анализа получим составляющие силы Кориолиса по осям координат.
Поверхностные силы. К поверхностным силам относятся те силы, которые действуют на соприкасающиеся поверхности слоя воздуха.
Сила давления (сила барического градиента) 
возникает за счет неравномерного распределения давления. Вектор силы барического градиента определяется соотношением
,
а его составляющие, отнесенные к единице массы, по осям координат, имеют следующий вид:
, 
, 
Сила трения 
возникает при движении воздуха, когда различные его объемы имеют разную скорость движения. Если рассматривать движение воздуха, как движение вязкой жидкости, то при движении двух соседних слоев жидкости с различными скоростями, между ними развиваются касательные силы внутреннего трения (касательное напряжение), или силы вязкости. Составляющие этой силы по осям координат:
, 
, 
.
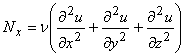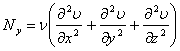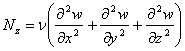- кинематический коэффициент турбулентной вязкости, а 
- динамический коэффициент вязкости.
5. Уравнение движения свободной атмосферы
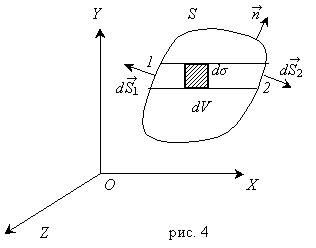
Как известно, плотность вещества в физике вводится предельным переходом: 
, где в механике сплошной среды следует понимать под Dm массу вещества, заключенную в объеме DW. Посмотрим, как будет выглядеть закон сохранения массы 
для произвольного подвижного объема сплошной среды, для которого 
. Из (1.12) тогда следует:
,
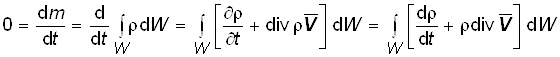или в силу произвольности объема W:
. (1.16)
Это уравнение носит название уравнения неразрывности (непрерывности).
Похожие работы
... Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4). В случае стационарных электрических и магнитных полей ( и) система уравнений Максвелла (1) – (4) распадается на систему уравнений электростатики: , , ...
... характере деформирования Расчет конструкций и их элементов с учетом всего многообразия физико-механических свойств реальных материалов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому, отказываясь от принятой в теоретической механике модели абсолютно твердого тела, в сопротивлении материалов приходится вводить свою модель — модель идеализированного ...
праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...
... заранее подготовленные учащимися доклады и рефераты по теме. Изложение темы можно завершить демонстрацией фильма «Плазма – четвёртое состояние вещества». 3. Перспективы в области изучение плазмы в школьном курсе. Возможные пути для изучения плазмы. Как я уже упоминал ранее, объём преподаваемого материала по теме «Плазма» крайне мал, даже по сравнению с тем же материалом за границей. ...
0 комментариев