Понятие устойчивости

Реферат

По физике

УСТОЙЧИВОСТЬ

Лекция 14.

Будем называть равновесное состояние устойчивым, если оно мало изменяется при малых возмущениях.

Приведём некоторые примеры.

1.  Тяжелый шар на поверхности, имеющей вершины, впадины и горизонтальные участки.

Устойчивое равновесное состояние   Безразличное состояние   Неустойчивое равновесное состояние

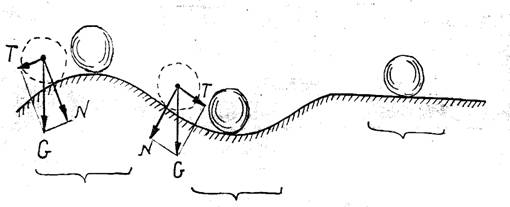В том случае, когда шарик находится на вершине, составляющая силы тяжести Т, возникающая при его отклонении, уводит его от первоначального состояния, для шарика, находящегося во впадине сила Т будет возвращать отклонённый шарик в первоначальное состояние и он будет колебаться в окрестности наиболее низкой точки впадины, т.е. при малых отклонениях состояние шарика будет также меняться мало. Случай шарика, находящегося на горизонтальной поверхности, будет случаем разграничивающим рассмотренные выше не устойчивые и устойчивые равновесные состояния. Такое состояние называется безразличным.

2. Хорошо знакомую картину разрушение образца при растяжении с образованием шейки можно трактовать, как потерю устойчивости цилиндрической формы образца.

По мере приближения состояния образца становится неустойчивой, образуется шейка и малым изменениям силы соответствуют значительные изменения конфигурации системы.

Рис. 98

3.  Центрально сжатый гибкий стержень

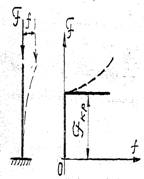
Предполагается, что стержень идеально прямой, а сила прилаженная строго по оси (что, конечно, практически невозможно).

Для того, чтобы судить устойчиво ли данное равновесное состояние, надо приложить горизонтальную возмущающую силу, которая вызовет прогиб. Если сила Р невелика, то прогиб окажется малым, равновесное состояние (прямолинейное) фактически не изменится . Однако если сила Р превысит некоторое значение называется критическим (F кр ), то равновесное состояние становится неустойчивым, т. е. любые малые возмущения приведут к значительным прогибам. Зависимость между прогибом и силой показана действительное поведение стержня, которое можно обнаружить с помощью нелинейных решений, сплошной чертой показано грубое, линейное решение задачи.

Задача Эйлера

Рассмотрим центрально сжатый шарнирно закрепленный с обоих концов стержень. Эта задача была решена Л. Эйлером.

Существо задачи состоит в том, что задача об устойчивости по отношению к заданному возмущению подменяется задачей о возможности существования двух различных форм равновесия при одном и том же значении силы F. Очевидно, что прямолинейная равновесная форма возможна (y = 0). Допустим, что наряду с прямолинейной равновесной формой возможна и криволинейная равновесная форма, показанная на рисунке.

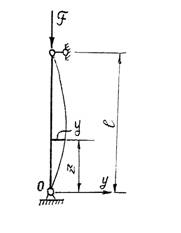
Кривизна стержня на основании закономерности известной из теории изгиба выразится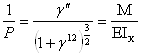

Будем полагать, что угол поворота y’ – величина малая по сравнению с единицей и тем более мал квадрат этой величины по сравнению с единицей

 

Изгибающий момент в произвольном сечении с координатой Z:  (знак минус увязывает прогиба и кривизны).

Дифференциальное уравнение изогнутой оси выглядит

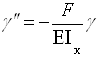 или   (1)

Решение этого дифференциального уравнения хорошо известно

Из граничных условий попробуем найти произвольные постоянные

C₁ и С₂

1)  при Z=0:

2)  при Z=:

Возможны две ситуации

C₁=0, откуда y0, т. е. получаем прямолинейную равновесную форму,

Sin K (nN) подставим в (1) выражение R² =  

 откуда найдем значение силы, при которой помимо прямолинейной равновесной формы появляется смежная криволинейная равновесная форма

реальный смысл имеет наименьшее значение силы при n=1 эйлерова сила – критическая сила.

F_кр=

Очевидно, что I_x – минимальный момент инерции.

Потери устойчивости будет происходить по синусоиде y = C₁Sin

однако произвольную C₁ мы так и не смогли найти.

Дело в том, что задача о потере устойчивости задача существенно нелинейно, а мы поступили непоследовательно. С одной стороны мы подошли к задаче как нелинейной, отойдя от принципа начальных размеров, и определив изгибающий момент с учетом изгиба стержня. С другой стороны, приняв приближенное выражение для кривизны, мы линеаризовали задачу. Для того, чтобы определить прогибы в закритической стадии надо исходить из нелинейного дифференциального уравнения.

Однако главная цель – определение критической силы для стержня нами достигнута.

Влияние условий закрепления концов стержня на величину критической силы

 

Формула (2) даёт возможность определить критическую силу только в том случае шарнирного опирания обоих концов стержня. Обобщим полученный результат на некоторые другие часто встречающиеся случаи закрепления.

а). Стержень, закреплённый жёстко одним концом и свободный от закрепления на другом. Очевидно изгиб стержня в этом случае будет таким же, как и в случае шарнирно опертого стержня, но имеющего длину в 2 раза большую.

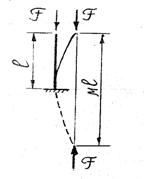
Критическая сила в этом случае будет равна критической силе шарнирно опёртого стержня, имеющего длину 2.

Введём понятие коэффициента привидения длины -  , т. е. числа показывающего во сколько раз нужно увеличить длину шарнирно опёртого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной  при заданном закреплении.

Очевидно, что в нашем случае коэффициент  можно трактовать , как число показывающее сколько раз длина стержня укладывается в длине полуволны синусоиды, по которой происходит потеря устойчивости.

Обобщим формулу Эйлера

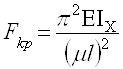(3)

Для некоторых других случаев закрепления коэффициент приведения длины равен:

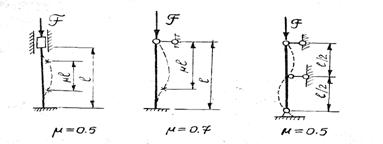
Рис. 102

Пределы применимости формулы Эйлера

Формула Эйлера выведена в предположении, что материал линейно упруг, и, естественно, применила, в тех случаях пока справедлив закон Гука.

Придадим формуле (3) иной вид.

Введём понятие критического напряжения, т. е. напряжения соответствующего критической силе.

;  (4)

но  где  - минимальный радиус инерции сечения.

Введём ещё одну величину – гибкость стержня.

, тогда

Тогда можно оказать, что формула Эйлера справедлива, если критические напряжения не превышают предела пропорциональности при сжатии.

Выясним при каких гибкостях можно использовать формулу Эйлера .

Приравняем в (4)

 =

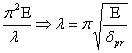
Если , то можно использовать формулу (3)

Для малоуглеродистых сталей, особенно часто используемых для сжатых элементов: МПа, E = 2*10⁵ МПа тогда,

 т.е. для малоуглеродистых сталей формулу Эйлера можно использовать при гибкостях больших 100.

Коэффициент запаса на устойчивость

Представляет собой отношение критической силы для стержня к силе, действующей на него.

Коэффициент запаса на устойчивость может выступать, некоторая заданная нормативная величина, тогда 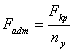 ,где F_adm– нагрузка допускаемая из условия устойчивости.

Пример.

Для заданного сжатого стержня определить допускаемую силу

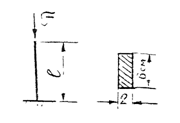
 = 50 см; материал Ст. 3

E = 2 10⁵ МПа;  = 210 МПа

n_y= 2

I_x = I_min = 4 см² ; A = 2*6 = 12 см²;

 = 2*50 = 100 см;

F_kp =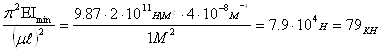

_{МПа; kpМПаМПаpr}

 

формула Эйлера применима

F_{adm =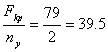}  кН

Расчет сжатых стержней на устойчивость по коэффициенту снижения допускаемых напряжений

Приведенное выше решение пригодно только для сравнительно длинных и тонких стержней. В случае коротких и жестких стержней потеря устойчивости происходит при возникновении пластических деформаций и задача требует специального рассмотрения. Существует решения (Т. Карман, Энгессер) об устойчивости стержня за пределами упругости. Иногда прибегают к эмпирическим формулам типа формулы Ясинского.

, где a и b-константы зависящие от свойств материала.

Изложим методику расчёта на устойчивость, предложенную русским инженером Ясинского в конце прошлого века. Суть этой методики состоит в том, что расчёт на устойчивость подменяется расчетом на обыкновенное сжатие, но допускаемые напряжения при этом полагаются переменными, зависящими от гибкости. Допускаемое напряжение на устойчивость полагается равным

- допускаемое напряжение при сжатии;

 - коэффициент снижения допускаемых напряжений. Он может трактоваться, как следующее отношение.

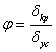
Коэффициент снижение допускаемых напряжений зависит от гибкости  

С увеличением гибкости величины его уменьшается.

Разумеется, что зависит не только от гибкости, но и от свойств материала. Для наиболее употребительных материалов он вычислен и приведён в таблицах. Приведем такую таблицу для ст. 3 материала наиболее часто применяемого для сжатых элементов.

0	1,00	110	0,52
10	0,99	120	0,45
20	0,96	130	0,40
30	0,94	140	0,36
40	0,92	150	0,32
50	0,89	160	0,29
60	0,86	170	0,26
70	0,81	180	0,23
80	0,75	190	0,21
90	0,69	200	0,19
100	0,60	---	---

Для промежуточных значений  соответствующие значения определяются путем линейной интерполяции.

Примеры.

Если известно сечение сжатого элемента, то нагрузку которую может воспринять стержень из условия устойчивости определяется.

N_{adm =}