Навигация
Определить величину допускаемой нагрузки на ферму из условия устойчивости поясов АВ и ВД
1. Определить величину допускаемой нагрузки на ферму из условия устойчивости поясов АВ и ВД.
Материал – Ст. 3, ![]() = 160МПа
= 160МПа
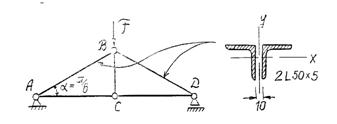
Рис. 104
Площадь сечения А = 2АL = 2*4,8 = 9,6 см2 ;
Минимальный момент инерции сечения будет
Ix= 2ILx
Минимальный радиус инерции
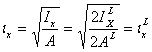
По сортаменту определяем ![]() =1,53см
=1,53см
Приведенная длина верхнего пояса
![]()
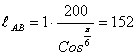 см
см
Гибкость ![]()
![]() по таблице
по таблице
Допускаемое усилие из условия устойчивости для стержня AB:
![]()
![]()
Свяжем между собой силу, действующую на ферму F и усилие NAB
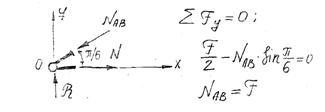
Рис. 105
Допускаемая нагрузка на ферму
Fadm=48.5кн
Другим типом задачи является подбор размером сечения заданного типа. Можно записать
A=![]()
Однако ![]() зависит от размеров и формы сечения, таким образом круг замыкается и задача может быть решена только методом попыток. По сути задача подбора сечения сводится к некоторой последовательности задач первого типа.
зависит от размеров и формы сечения, таким образом круг замыкается и задача может быть решена только методом попыток. По сути задача подбора сечения сводится к некоторой последовательности задач первого типа.
2. Подобрать размеры квадратного поперечного сечения для сжатого стержня. F=280кн. Материал Ст.3 ![]() =160МПа:
=160МПа: ![]() =1м. Разберемся с геометрическими характеристиками
=1м. Разберемся с геометрическими характеристиками
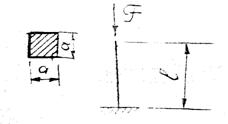
Рис. 106
A=a2 ; Ix=![]() ;
; ![]()
1) ![]()
![]() см
см
a=![]() см;
см; ![]() см2;
см2;
Нагрузка, которую может воспринять сечение при заданных размерах
![]()
Размеры сечения слишком велики
2)![]()
![]() см
см
a=![]() см; A=24см2;
см; A=24см2;
![]()
Размеры сечения слишком малы
3) Т. к. в обоих случаях мы оказались далеки от истины, то попробуем в качестве следующего значения ![]() среднее арифметическое из первых двух
среднее арифметическое из первых двух
![]()
![]()
![]() см; a =
см; a =![]() см; A=36см2;
см; A=36см2;
![]() кн
кн
Обычно считается, что результат достигнут, если сила, которую воспринимает сечение отличается от действующей силы не более чем на 5% в ту или другую сторону т. е.
0,95F ![]()
В нашем случае это условие выполнено.
Принимает размер сечения a = 6см
Лекция 15
Энергетический способ определения критических сил
В сколь-нибуть сложных случаях, получить критическую силу из решения дифференциального уравнения изогнутой оси сжатого стержня затруднительно.
Поэтому в подобной ситуации проще получить приближённое решение, например, энергетическим методом.
Рассмотрим стержень центрально сжатый силой F. Условно на рисунке стержень показан шарнирно опёртым, но вопрос о граничных условиях пока оставим открытым
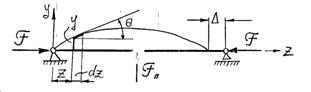
Рис. 106
Пусть сила F меньше эйлеровой критической силы. Если приложить к стержню некоторую поперечную нагрузку Fп, то стержень изогнётся, но будет находиться в устойчивом равновесном состоянии. Сжимающая сила совершит при этом работу на перемещении ▲, которое можно найти следующим образом.
Укорочение малого элемента длиной dz будет равно
![]() ▲=
▲= ![]()
учтём, что ![]() = y'
= y'
Тогда ▲=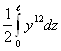
Потенциальная энергия деформации изогнутого стержня
U=
Здесь учтено, что M = EIxy”
Изменение полной энергии при малом изгибе будет
![]()
Если ![]() , то стержень устойчив, если же
, то стержень устойчив, если же ![]() , т.е. F
, т.е. F![]() производит работу большую, чем может на копиться в стержне в виде энергии упругой деформации, избыточная работа идёт на сообщение кинетической энергии, стержень приходит в движение и прогибается дальше. Т.е. он не устойчив. Очевидно, что когда сила достигает критического значения, то Fкр
производит работу большую, чем может на копиться в стержне в виде энергии упругой деформации, избыточная работа идёт на сообщение кинетической энергии, стержень приходит в движение и прогибается дальше. Т.е. он не устойчив. Очевидно, что когда сила достигает критического значения, то Fкр![]() или
или
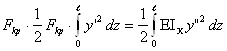 откуда
откуда
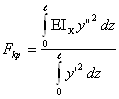
Для получения значения критической силы необходимо задаться формой изогнутой оси. Функцию y = y(z) надо подбирать таким образом, чтобы она удовлетворяла граничным условиям.
Примеры1) Вначале попробуем решить рассмотренную ранее задачу о критической силе для шарнирно опёртого по обоим концам стержня. Точное решение известно.
Fkp = ![]()
Форма изогнутой оси в этом случае известна
y = CSin![]()
но предположим, что это нам не известно и аппроксимируем изогнутую ось полиномом четвёртой степени
![]()
Граничные условия следующие
А) при Z = 0: y=0 (1) ; y”=0 (2) прогиб равен нулю и момент равен нулю,
Б) при Z = ![]() : y = 0 (3) ;y”=0 (4)
: y = 0 (3) ;y”=0 (4)
Возьмём производные
y’ = 4Az3+3Bz2+2Cz+D;
y” = 12 Az2+6Bz+2C
Из (1) E = 0 ; bp (2) C = 0 Используем (3) ![]() ; из (4) следует
; из (4) следует
12 A![]() подставляя в (3): A
подставляя в (3): A![]()
D=A![]() y’=A(4z3-6
y’=A(4z3-6![]() ; y”=12A(z2-
; y”=12A(z2-![]()
Подставим эти выражения в формулу (1)
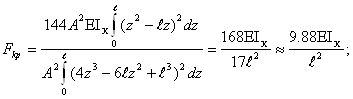
Как видим, приближённое решение практически не отличается от точного.
2)Рассмотрим более сложную задачу.
Определить критическую силу для стержня , показанного на рисунке.
Аналогично предыдущему случаю, аппроксимируем изогнутую ось полиномом
y = Az4+Bz3 +Cz2 +Dz+E
Запишем граничные условия
1) при z = 0 y = 0 (1)
y’ = 0 (2)
2) при z =3![]() : y” = 0 (свободный конец и момент отсутствует) (4)
: y” = 0 (свободный конец и момент отсутствует) (4)
Найдем производные
y' = 4Az3+3Bz2+2Cz+D
y” = 12Az2+6Bz+2C;
Используем граничные условия
Из (1) E = 0 ; из (2) D = 0
Из (3) A16![]() 4+B8
4+B8![]() 3+C4
3+C4![]() =0
=0
4![]() 2A+2
2A+2![]() B+C=0 (3а)
B+C=0 (3а)
Из (4) 12A*9![]() 2+6B*3
2+6B*3![]() +2C=0
+2C=0
54![]() 2A+9
2A+9![]() B+C=0 (4а)
B+C=0 (4а)
Решим совместно (3а) и (4а)
_9![]() B+C=-54
B+C=-54![]() 2A
2A
2![]() B+C=-4
B+C=-4![]() 2A
2A
------------------------
7![]() B=-50
B=-50![]() 2A B=
2A B=![]() ;
;
C=-4![]() 2-2
2-2![]() (
( ![]() )=
)=![]()
Подставим найденные значения коэффициентов полинома в выражения для
y’=2A(2z3-![]()
![]() z2+
z2+![]() )
)
y” = 12A(z2-![]()
![]() z+
z+![]() .
.
Подставим в (1)

Вычисляя интеграл, получаем
Fkp![]()
Похожие работы
... / Под ред. А.Д. Урсула. — М.: Издательство РАГС, 2001 Перелет. 6. Р.А. Выявление показателей устойчивого развития // Проблемы окружающей среды и природных ресурсов. ВИНИТИ — 1995. — № 6. Содержание Введение 1. Сущность и понятие государственного долга 1.1 Формы и виды 1.2 Управление государственным долгом 2. Пути урегулирования внешнего госдолга Заключение Список используемой литературы ...
... и государства за создание условий для будущих поколений удовлетворять разнообразные потребности – физиологические, экономические, духовные и иные – в процессе взаимодействия с природой. Формирование и реализация концепции устойчивого развития, имеющей фундаментальное значение, не может происходить без определенных, в том числе существенных, трудностей. Однако, несмотря на это мировое сообщество, ...
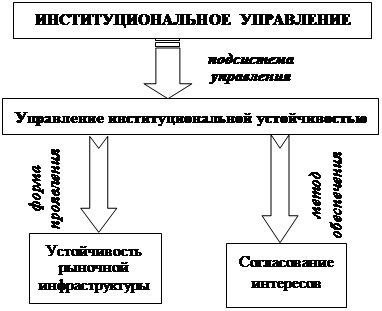
... процессов. Формирование институтов согласования интересов хозяйствующих субъектов на основе осуществления медиаторской деятельности, выступающей механизмом обеспечения институциональной устойчивости социально-экономической системы, наиболее значимо для экономических систем регионального уровня, что определяется спецификой организационно-управленческих связей хозяйственных образований данного ...
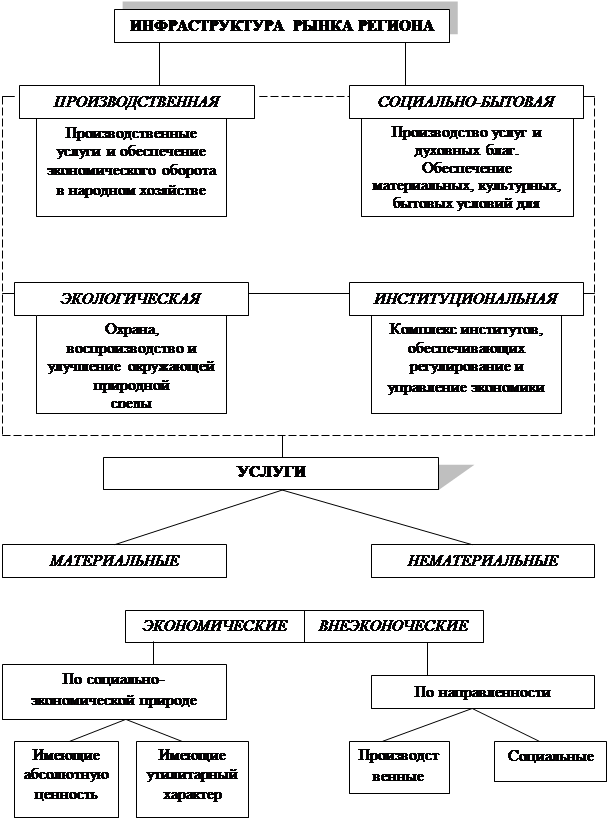
... базовых функций управления (организации, планирования), а с другой – самостоятельная функция управления, так как деятельность по обеспечению устойчивости представляется довольно автономным видом управленческой активности. Наиболее значимые направления по обеспечению институциональной устойчивости сферы сервиса проявляются в следующих функциях: – технологическая функция заключается в ...




0 комментариев