Навигация
Эффекты, связанные с постоянством скорости света в инерциальных системах
3. Эффекты, связанные с постоянством скорости света в инерциальных системах
Предварительное замечание. Световой луч всегда порождается своим источником. В системе отсчета, где этот источник покоится, отсутствуют явления аберрации света, эффект Доплера и др. явления. Систему отсчета, связанную с источником света, мы будем называть «базовой системой». Если имеется среда (диэлектрик, замедляющие структуры и пр.), то для волны, отраженной, проходящей или рассеянной средой, такой базовой системой отсчета будет служить эта среда. Она является как бы источником «вторичного излучения». Иными словами, источником света, отраженного от зеркала, будет служить само зеркало (независимо от того, движется оно или же покоится в рассматриваемой системе), а не первичный источник света, падающего на зеркало. Если не будет оговорено специально, то величины, относящиеся к базовой системе отсчета, мы будем маркировать штрихами.
Математический формализм специальной теории относительности включает в себя понятие «истинный скаляр». Истинный скаляр есть величина, которая сохраняется инвариантной при применении преобразования Лоренца или модифицированного преобразования. Он имеет сущностный характер. Проекции отрезка (истинного скаляра) на оси пространственно-временных координат в любой системе отсчета относятся к разряду явлений.
Если, например, неподвижный пространственно-временной отрезок мы будем рассматривать из движущейся системы отсчета, то его длина, определяемая квадратичной формой будет одна и та же. Она является истинным скаляром. Однако проекции на оси координат в разных системах отсчета будут отличаться.

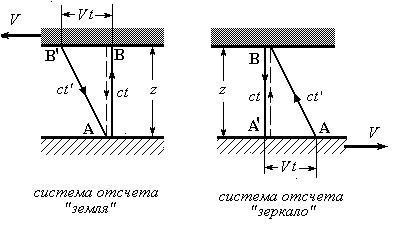
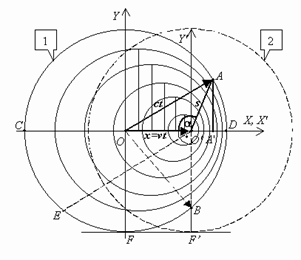
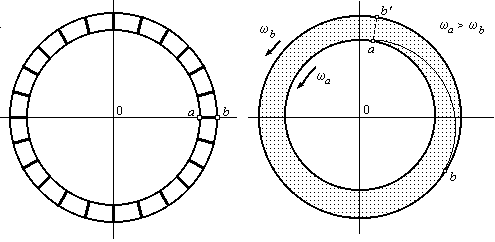
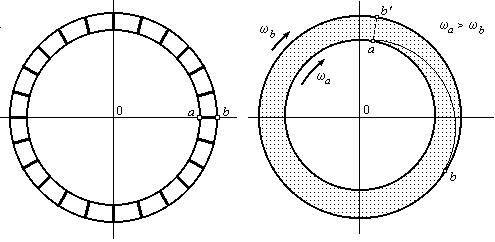
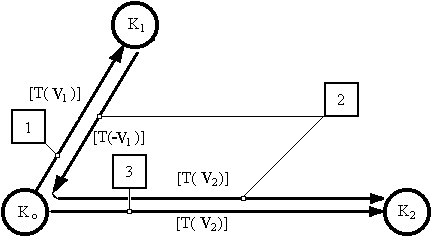
А. Интервалы времени и длины отрезков в разных ИСО. Рассмотрим неподвижный пространственный отрезок АВ (левый фрагмент рис. 3), ориентированный вдоль оси х’. Концы этого отрезка имеют проекции на эту ось x’1 и x’2. В момент времени t’0 мы осветим весь этот отрезок на короткое мгновение. Наблюдатель, расположенный в движущейся системе (x, ct), увидит, что в точке x1 в момент времени t1 возникнет световая точка, которая будет перемещаться к координате x2, которую она достигнет в момент времени t2 .

Рис. 3
Можно ли рассматривать пространственный интервал (х1÷х2) как «длину» движущегося отрезка? Конечно нельзя! Действительная длина отрезка остается неизменной. Она не зависит от выбора наблюдателем системы отсчета. Информация, передаваемая с помощью светового луча, как мы видим, искажается. Появляется отличная от нуля проекция на ось времени (ct1÷ct2), которая в собственной системе отсчета отрезка была равна нулю. Действительная же длина отрезка инвариантна. Она определяется, приведенной выше квадратичной формой.
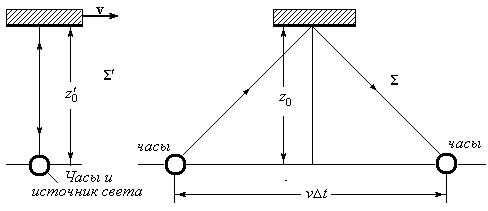
Аналогичные явления имеют место, когда мы рассматриваем интервал времени. Если в неподвижной точке x’0 на короткое время t’1 ÷ t’2 вспыхивает лампочка, интервал времени (отрезок CD на правом фрагменте рис. 3), то движущийся наблюдатель обнаружит, что светящаяся точка перемещается в пространстве от х1 к точке х2 за время ct1 ÷ ct2. Но это время перемещения не есть действительный «интервал времени», наблюдаемый в движущейся системе. Это проекция.
Итак, мы обнаружили еще один миф о «замедлении времени» и «сжатии масштабов» в теории относительности. Никаких «сжатий» и «замедлений» в движущейся системе нет. Есть только наблюдаемые явления. Это искаженное отображение реальности, полученное с помощью световых лучей.
Б. Эффект Доплера. Как известно, истинные скаляры («сущности») остаются инвариантными в любой инерциальной системе отсчета. Таким инвариантом является фаза волны, регистрируемая наблюдателем. Для монохроматического сигнала в системе отсчета наблюдателя, когда наблюдатель движется относительно источника в плоскости (x’; y’) мы можем записать
Ф = w’t’ – k’x’cosq’ - k’y’sinq’(3.1)
где ω' – циклическая частота колебаний источника, k' = ω'/c – волновое число (предполагается, что волна распространяется в вакууме), а q’– угол между направлением наблюдения и скоростью относительного движения источника и наблюдателя V (осью 0x) в K'
В системе отсчета движущегося наблюдателя (система К) мы можем записать
Ф = wt – kxcosq - kysinq(3.2)
Выражение (3.2) должно получаться из (3.1) путем замены x', y' и t' на x, y и t в соответствии с модифицированным преобразованием. Имеем

Это выражение можно привести к следующему виду
![]() (3.3)
(3.3)
Сравнивая (3.2) и (3.3) и учитывая, что k = w/с; k’ = w’/с, получаем
 (3.4)
(3.4)
Выражая угловую частоту через не штрихованные величины, получаем выражение для наблюдаемой частоты в системе отсчета неподвижного наблюдателя
 (3.5)
(3.5)
где V – действительная скорость относительного движения инерциальных систем отсчета, входящая в модифицированное преобразование, и v – скорость, входящая в преобразование Лоренца. Эта формула описывает эффект Доплера.
В. Аберрация. Аберрация света связана с искажением фронта световой волны, который возникает при переходе из системы отсчета, связанной с источником, к системе отсчета, связанной с движущимся относительно источника наблюдателем.

Рис. 4
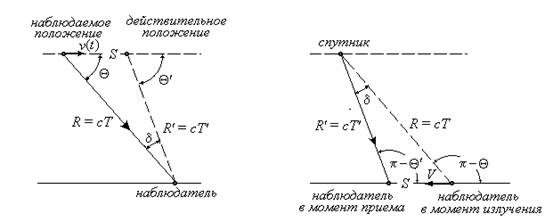
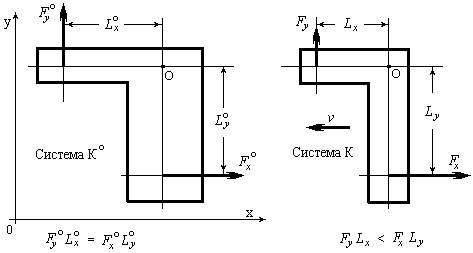
Рассмотрим поведение световых лучей в двух системах отсчета. В системе отсчета, связанной с источником излучения, мы имеем два отрезка ON’ и ON. Первый отрезок ON’ соответствует реальному пути, пройденному светом до встречи с наблюдателем N’. Второй отрезок ON равен действительному расстоянию от источника света O до наблюдателя N в момент излучения светового импульса (Рис. 4 слева).
В системе отсчета наблюдателя (рис. 4 справа) мы имеем такие же два отрезка O’N и ON. Первый отрезок O’N есть действительное расстояние, пройденное лучом от источника до наблюдателя. Второе расстояние ON – расстояние, фиксируемое наблюдателем (кажущееся) расстояние. Оно искажено из-за конечной скорости распространения волны и определяет эффект «деформации» светового луча. На нем мы сейчас остановимся. Угол аберрации равен разности углов δ = q’ - q. Треугольники ONN’ и NOO’ равны, поскольку отрезок VT одинаков в обеих системах отсчета. Соответственно, углы аберрации одинаковы в этих системах.
Г. «Деформация» отображения пространственных отрезков. Продолжим анализ явления аберрации. Обратимся к рис. 4. В системе отсчета, связанной с излучающим объектом, световой луч, распространяясь без искажений, проходит расстояние R’. Это расстояние на рис. 4 слева отображено отрезком ON’. Направление светового потока идет под углом q’0 по отношению к вектору скорости.
В системе отсчета, связанной с наблюдателем этот отрезок «деформируется». Наблюдателю будет казаться, что световой луч подходит к нему под углом q, а расстояние, которое он проходит со скоростью света, будет иным (отрезок ON на рис. 4 справа). Отношение наблюдаемого расстояния ON к действительному (не искаженному движением) расстоянию O’N мы будем называть «коэффициентом деформации». Поскольку скорость света в любой системе отсчета одинакова, этот коэффициент будет пропорционален отношению времен распространения света вдоль этих направлений
![]() (3.6)
(3.6)
Формула (3.6) описывает явление «деформации» в системе отсчета наблюдателя, движущегося относительно источника. Наблюдателю будет казаться, что свет прошел иное расстояние, отличное от действительного. Этот эффект, откровенно говоря, релятивисты «проморгали».
Еще одна закономерность:
Расстояние R (см. рис. 4) равно расстоянию между наблюдателем N и источником светового сигнала O в момент излучения сигнала источником. Расстояние R’ отвечает расстоянию между O и N’ или O’ и N в момент приема сигнала наблюдателем.
Итак, постоянство скорости света в вакууме и независимость этой скорости от выбора инерциальной системы отсчета (требуемое принципом А. Пуанкаре) не противоречит классическим пространственно-временным отношениям. В силу этого можно дать непротиворечивое описание световых явлений в рамках классических представлений о пространстве и времени и опираясь на модифицированное преобразование.
4. Закон «преломления» светового луча
А. Закон "преломления" светового луча. Критики СТО ограничиваются, как правило, анализом эффектов "сокращения" масштабов движущихся тел и "замедлением" времени. К сожалению, они не принимают во внимание, что движущийся объект пролетает мимо них с наблюдаемой скоростью v(t), и наблюдатель по мере движения объекта вынужден рассматривать его под различными углами наблюдения q. При этом возникает ряд интересных явлений, с частью которых мы уже познакомились.
Угол наблюдения q образован двумя векторами: вектором скорости движущегося тела и вектором, направленным вдоль светового луча от движущегося источника к наблюдателю. Теоретически он может меняться от 0 до 180 градусов в системе отсчета, связанной с наблюдателем. В системе отсчета, связанной с движущимся объектом, этот луч будет иметь другое направление, т.е. идти под другим углом q' (меняясь тоже от 0 до 180 градусов).
Из преобразования Лоренца известны следующие соотношения:

где: f и f ' частоты принимаемого и излучаемого сигналов соответственно.
Запишем теперь угол расхождения между лучами (угол аберрации), который нам понадобится в дальнейшем:

Допустим, что движущийся объект это линейка длиной Dx', ориентированная вдоль вектора скорости V. Нетрудно видеть, что наблюдаемая длина линейки будет зависеть от V и q. Кажущаяся длина линейки есть (2.5):
 .
.
Формула, связывающая Dx и Dx', позволяет получить очень важное соотношение, которое можно назвать законом "преломления". Для этой цели умножим Dx на sinq и преобразуем это произведение.
 (4.1)
(4.1)
Физический смысл полученного выражения можно проиллюстрировать рис. 5.

Рис 5.
Величина d это толщина светового луча. Она сохраняется постоянной в любой инерциальной системе отсчета. Если учесть, что ширина этого луча не зависит от выбора инерциальной системы отсчета, можно сформулировать закон "преломления" света при переходе наблюдателя из одной инерциальной системы отсчета в другую:
При переходе наблюдателя из одной системы отсчета в другую световой луч не меняет своего сечения; он поворачивается на угол аберрации d = q' - q.
Б. Наблюдаемая форма движущегося объекта. Полученное соотношение можно с успехом использовать для описания видимой формы движущегося объекта. Пусть мимо нас со скоростью V, параллельной оси x, пролетает куб, ориентированный по осям x,y,z или x',y',z'. Пусть лучи от неподвижного куба размером а х а направлены в точку встречи с наблюдателем под углом q’ (рис. 6А).

Рис. 6
Если куб находится очень далеко от нас, то человеческий глаз увидит плоское изображение. Однако если человек знает, что форма предмета куб, его мозг быстро восстановит "изображение". Наблюдателю будет казаться, что летящий куб "развернут" на угол d по отношению к своей истинной ориентации (рис. 6 В).
Отметим следующее:
1. Наблюдаемая форма куба сохраняется, но изображение будет поворачиваться при изменении угла наблюдения на угол d(q). Ориентация куба в движении вдоль оси х напоминает фигуру высшего пилотажа под названием "кобра". Наибольший наблюдаемый «поворот» куба будет при критическом угле наблюдения. Это напоминает во многом явление либрации.
2. Пусть цвет куба зеленый, а его скорость порядка 0,7с. Цвет куба при изменении угла наблюдения будет меняться от фиолетового при малых углах и до красного больших скоростях. Изменение цвета - явление, известное под названием эффект Допплера.
Описанная выше визуальная форма движущегося куба есть сугубо субъективное явление, полученное при участии головного мозга. Это субъективная кажимость (как говорят: "обман зрения"). Теперь необходимо рассмотреть объективную кажимость (объективное явление), т.е. то, что мы будем измерять на самом деле, например, с помощью оптического дальномера.
В. Измеряемая форма движущегося объекта. Оставим в стороне иллюзии, связанные с субъективным человеческим восприятием (оптической иллюзией). Реальная форма объекта может быть получена методами радиолокации или иными объективными оптическими методами измерений расстояния с помощью световых лучей или электромагнитных волн. Однако нам нет необходимости использовать столь сложные средства, поскольку мы знаем закон "преломления" светового луча. Результаты измерений покажут, что (рис. 6 С):
Похожие работы
... наблюдаемого объекта. Итак, мы познакомились с теми явлениями, которые вытекают из свойств модифицированного преобразования или преобразования Лоренца. Мы описали и те явления, на которые Специальная теория относительности А. Эйнштейна «не обратила» внимания. Теперь мы можем перейти к «мысленным экспериментам» А. Эйнштейна. 3. Слово о «мысленных экспериментах» Во-первых, все исследования мы ...
... преобразования Лоренца так же могут быть получены из требований инерциальности рассматриваемых систем отсчета (дробно линейные преобразования Лоренца-Фока). Из этого же требования вытекает постоянство скорости (света) объектов, координаты которых связывают эти преобразования в различных системах отсчета. Далее, основываясь на анализе преобразований Лоренца, будут установлены причинно-следственные ...
... до того, что начали овеществлять время и даже придумали частицу времени – хронон. С позиций нового (или восстановленного древнего) определения времени теряют право на жизнь преобразования Лоренца и ставшая уже привычной четырехмерная размерность пространства-времени, о чем будет показано ниже. На смену им приходят новые преобразования и полностью симметричное шестимерное пространство-время (хотя ...
... дать логически последовательное объяснение парадоксам и прикрывают его фиговыми листочками математических формул, мы вскрываем застарелые «язвы», разъедающие СТО и физику. Наш научный задел размещен на сайте [14]. Новый подход к объяснению релятивистских явлений возвращает нас к классической механике Ньютона. Новый подход к релятивистским явлениям затронет и классическую электродинамику. Причина ...
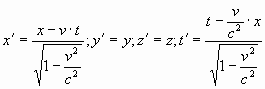
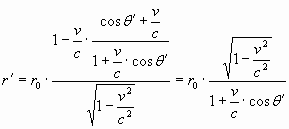
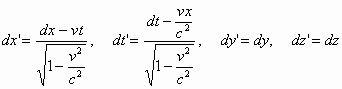
0 комментариев