Определение удельных нагрузок на провод и трос

4.2 Определение удельных нагрузок на провод и трос

Удельная нагрузка от собственного веса, даН/(м∙мм2), берется из таблиц 2.1 и 2.2:

3,46·10-3;

8·10-3.

Удельная нагрузка от веса гололеда, даН/(м∙мм2),

, (4.8)

где d – диаметр провода или троса, мм;

F – фактическое сечение провода или троса, мм2;

g0=0,9·10-3 даН/(м∙мм2) – плотность гололедных отложений;

=4·10-3;

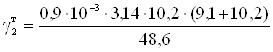=11,4·10-3.

Удельная нагрузка от веса гололеда и собственного веса провода (троса), даН/(м∙мм2),

, (4.9)

·10-3=7,46·10-3;

·10-3=19,4·10-3.

Удельная нагрузка от давления ветра при отсутствии гололеда, даН/(м∙мм2),

, (4.10)

где kl – коэффициент, учитывающий влияние длины пролета на ветровую нагрузку;

kH – коэффициент, учитывающий неравномерность скоростного напора ветра по пролету;

СХ – коэффициент лобового сопротивления, равный 1,1 – для проводов диаметром 20 мм и более, свободных от гололеда; 1,2 – для всех проводов, покрытых гололедом, и для проводов диаметром меньше 20 мм, свободных от гололеда;

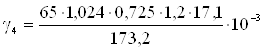=5,7·10-3;

=13,1·10-3.

Удельная нагрузка от давления ветра на провод и трос при наличии гололеда, даН/(м∙мм2),

, (4.11)

где q′=0,25∙qmax для районов с толщиной стенки гололеда до 15 мм;

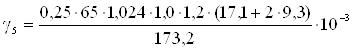=4,1·10-3;

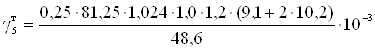=15,1·10-3.

Удельная нагрузка от давления ветра и веса провода (троса) без гололеда, даН/(м∙мм2),

, (4.12)

·10-3=6,7·10-3;

·10-3=15,3·10-3.

Удельная нагрузка на провод от давления ветра и веса провода, покрытого гололедом, даН/(м∙мм2),

 (4.13)

=8,5·10-3;

=24,6·10-3.

4.3 Расчет критических пролетов

Первый критический пролет, м,

, (4.14)

где Е – модуль упругости, даН/мм2;

α – температурный коэффициент линейного удлинения материала провода, град-1;

lk1=.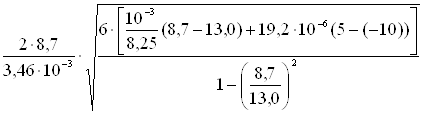

Выражение под корнем меньше нуля. Первый критический пролет – мнимый.

Второй критический пролет, м,

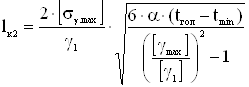, (4.15)

где tгол – температура гололеда, равная -5ºС;

γmax=γ7;

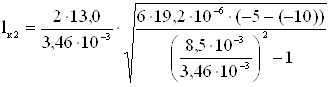=80,4.

Третий критический пролет, м,

, (4.16)

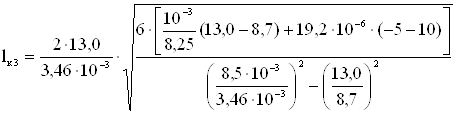=144,2.

В результате получается следующее соотношение критических пролетов и расчетного пролета: lк1 – мнимый, lр=202,5 м>lк3=144,2 м.

На основании полученных соотношений определяется исходный режим. Это режим максимальной нагрузки с параметрами: σ=[σγ.max]=13,0 даН/мм2, γ=γmax=8,5·10-3 даН/(м·мм2), t=tгол=-5°С.

4.4 Расчет напряжений в проводе

По уравнению состояния провода рассчитываются напряжения в проводе для режимов среднегодовой температуры – σtср, режима низшей температуры – σtmin и наибольшей нагрузки – σγmax.

Расчет напряжения в проводе для режима низшей температуры. В уравнение состояния провода подставляются все известные параметры.

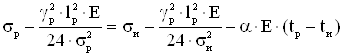, (4.17)

.

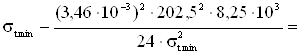
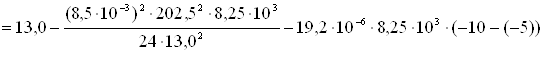Полученное уравнение приводится к виду:

Решение полученного уравнения выполняется итерационным методом касательных. В качестве нулевого приближения принимается значение σ0=10 даН/мм2.

Производная полученной функции y=:

y’=3·σ2tmin-2·7,766·σtmin

Определяется поправка на первой итерации:

Δ1=y(σ0)/y’(σ0),

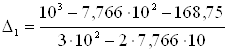=0,378.

Новое значение напряжения:

σ1=σ0-Δ1,

σ1=10-0,377=9,623.

Проверка итерационного процесса. Для этого задается точность расчета ε=0,01 даН/мм2.

0,377>0,01,

следовательно расчет нужно продолжить, приняв в качестве нового приближения σ=9,623.

Поправка на второй итерации:

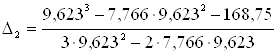=0,025.

Новое значение напряжения:

σ2=9,623-0,025=9,598.

Выполняется проверка:

0,025>0,01.

Поправка на третьей итерации:

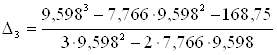=0,00013.

Проверка:

0,00013<0,01,

следовательно за искомое выражение σtmin принимаем σ3:

σtmin=9,598 даН/мм2.

Расчеты напряжений в проводе для режимов среднегодовой температуры и наибольшей нагрузки выполняются с помощью программы «MERA2». В результате получены следующие значения:

σtср=7,987 даН/мм2;

σγmax=12,517 даН/мм2.

Выполняется проверка условий механической прочности:

σtср≤[σtср], 7,987<8,7;

σtmin≤[σtmin], 9,598<13,0;

σγmax≤[σγmax], 12,517<13,0.

Условия выполняются, значит механическая прочность проводов будет достаточной для условий проектируемой линии.

По уравнению состояния провода выполняются расчеты напряжений для режимов гололеда без ветра –σгол, высшей температуры – σtmax, грозового режима – σгр. Результаты расчетов следующие:

σtmax=5,475 даН/мм2;

σгол=12,277 даН/мм2;

σгр=7,129 даН/мм2.