Навигация
1. Теоретическая часть
Для материальной точки массой m, вращающейся по окружности радиусом r
момент инерции определяется по формуле J=mr2. Для протяженных тел правильной формы его величину вычисляют с применением
теоремы Гюйгенса-Штейнера или методов дифференцирования и интегрирования.
Рис.1. Моменты инерции некоторых тел для указанных осей вращения.
Диск (цилиндр) J=mr2/2. Стержень J=ml2/12. Пластина размером аxb J=m(a+b)2/12.
Обруч J=mr2. Диск J=mr2/4
Если закрепить тело на упругом подвесе и, придав ему начальное угловое смещение, отпустить, то оно начнет совершать крутильные колебания вокруг подвеса, как оси вращения. Период таких колебаний зависит от момента инерции J и модуля упругости кручения D подвеса:
T=2π√(J/D), (1) откуда J=T2D/4 π2. (2)
Последней формулой можно пользоваться для сравнения моментов инерции разных тел. Чтобы получить численные значения моментов инерции произвольных тел необходимо предварительно вычислить момент инерции используемой в работе прямой шинки. Для этого воспользуемся формулой J0=ml2/12, и известными массой ( m= г) и длиной (l= см). В последующем опыт проводят с одним и тем же подвесом (D=const), поэтому можно пользоваться соотношением
J=Jo(T/To)2, (3) где Jo= г∙см2.
2. Экспериментальная часть
Задание 1. Зависимость момента инерции от массы тела.
Подвес – медная проволока диаметром 0.4 мм и длиной 30-40 см. Исследуемое тело - медная шинка длиной 30 см. Закрепите подвес как можно ближе к центру тяжести шинки. Запустите крутильный маятник, определите время t полных десяти колебаний и вычислите период Tо=t/10.
Прикрепите (скотчем) к первой вторую медную шинку такой же длины и вновь определите период колебаний Т2. По формуле (3) вычислите момент инерции J2. Найдите отношение моментов J2/Jо сравните с отношением масс m2/mo=2. Сделайте вывод о виде зависимости момента инерции тела от его массы.
Задание 2. Зависимость момента инерции тела от распределения его массы.
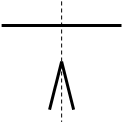
Изогнув шинку так, как показано на рисунке, измените распределение массы вдоль ее радиуса вращения. Определите период колебаний такой шинки и, сравнив его с периодом колебаний прямой шинки, сделайте вывод о том, как зависит момент инерции тела от распределения его массы.
Примечание: В первом случае расстояние от оси вращения до центров тяжести левой и правой половин шинки равно ј ее длины; во втором – зависит от угла изгиба. Рассчитайте эти расстояния самостоятельно для углов 60 и 30 градусов и свяжите эти размеры с моментами инерции.
Задание 3. Зависимость момента инерции тела от положения в нем оси вращения.
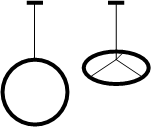Объект исследования - металлическое кольцо. Вначале закрепите его так, чтобы ось вращения совпадала с осью кольца (см. рис.) и определите период колебаний. Затем измените точку крепления так, чтобы ось вращения лежала в плоскости кольца, и вновь определите период колебаний. Сравните полученные значения и сформулируйте ответ на вопрос, поставленный в задании.
Задание 4-а. Адитивность момента инерции.
Соберите (при помощи скотча) составное тело из кольца и прямой шинки. Определите период колебаний и, сравнив с периодом колебаний прямой шинки, определите момент инерции составного тела. Сравните полученный результат с моментами инерции шинки и кольца. Сделайте вывод из полученных результатов.
Задание 4-б. Закрепляя на прямой шинке шарики одинаковой массы симметрично относительно ее центра тяжести, проверьте, выполняется ли закон сложения моментов импульса системы тел.
Задание 5. Момент импульса вращательного движения. Опыты с гироскопом и на скамье Жуковского. (Проводятся в форме демонстраций с пояснениями)
Контрольные вопросы
1. Что является мерой инертности в поступательном движении? В колебательном? Во вращательном?
2. Как рассчитывается момент инерции материальной точки?
3. Как записывается второй закон динамики для вращательного движения?
4. Что такое момент силы? Как он направлен?
5. Какие величины используют для описания вращательного движения?
6. Что такое период колебаний? Каковы единицы его измерения?
7. Как момент инерции зависит от массы тела?
8. Как распределение массы тела вдоль радиуса вращения влияет на момент инерции?
9. Сколько моментов инерции у обруча? у стержня? у цилиндра?
10. Как спортсмен, прыгая с трамплина в воду, управляет скоростью своего вращения?
11. Что собой представляют гиродины космического корабля? Как они действуют?
12. От чего и как зависит кинетическая энергия вращающегося тела?
1.2. Примечание: Конец наклонной плоскости можно немного загнуть так, чтобы влет тела происходил горизонтально. Это облегчает дальнейшие расчеты.
[3] Полученный ряд числовых значений укладывается в простую закономерность: А1/А2 = А2/А3 = А3/А4 = ….. = λ, где λ – декремент затухания.
Похожие работы
... Сербо «Сборник задач по теоретической механике», - М.: «Наука», 1977 г., - 320 с. И.В. Мещерский «Сборник задач по теоретической механике», - М.: «Наука», 1986 г., - 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», - М.: «Высшая школа» 1984 г., - 319 с. Студент-практикант: Филатов А.С.7 “Согласовано” “Утверждено” Преподаватель Джежеря ...
... школы. Мебель кабинета физики. Особенности оснащения и оборудования кабинета физики сельской школы. Рабочее место ученика и учителя в кабинете физики сельской школы. Кабинет физики в условиях разноуровневого обучения. Системы освещения и затемнения кабинета. Экскурсия в кабинет физики городской школы. 4. Работа заведующего кабинетом физики (5ч.) Права и обязанности заведующего кабинетом физики. ...
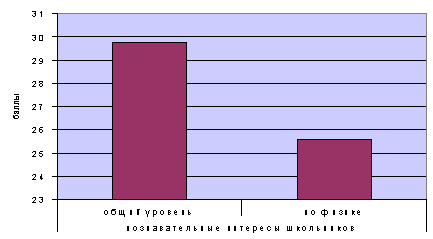
... и устаревание большинства разработок, способствующих развитию интереса к физике в школе вообще, и в частности - познавательного интереса при изучении физики на уроках. Объектом исследования является учебный процесс по физике в 9-м классе основной школы по теме "Законы сохранения в механике". Предмет исследования: практическая деятельность учителя на уроках физики по созданию условий и ...
... -педагогическая или научно-техническая проблема, являющаяся новым научным вкладом в теорию определенной области знаний (педагогику, технику и другие). 4. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ БАКАЛАВРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ПРОФИЛЬ ИНФОРМАТИКА 4.1. Положение о выпускной квалификационной работе бакалавра физико-математического образования: ...
0 комментариев