Методы обработки результатов косвенных измерений

5. Методы обработки результатов косвенных измерений

Косвенные измерения − это измерения, результат которых определяют на основании прямых измерений величины, связанной с измеряемой величиной известной зависимостью (известными математическими формулами).

Уравнение косвенных измерений имеет вид

y=f(x1, x2, …xn)

где y − искомая величина, являющаяся функцией величин x1, x2 … xn , полученных методом прямых измерений.

На практике для определения искомой величины зачастую необходимо иметь результаты нескольких независимых наблюдений величин x, y, z, которые образуют функцию f = f(x, y, z).

Функция f предполагается дифференцируемой по всем переменным, а также предполагается, что на интервалах, куда попадают значения x, y, z функции f не имеет нулей частных производных.

Обозначение функции fi = f(xi, yi, zi)

Существуют два метода обработки результатов косвенных измерений:

− метод переноса погрешностей;

− выборочный метод.

Обработка результатов измерений методом переноса погрешностей.

Этот метод используется в случае, когда каждая из величин x, y, z, представляющих собой аргументы функций, измеряется независимо от остальных в своей серии опытов, и эти величины организуют выборку (или они близки друг к другу). Число опытов в сериях не обязательно должно быть одинаково, но обязательным условием остается неизменность условий для прямого измерения величин в своей серии, неизменность условий для f во всех сериях и взаимная независимость всех опытов.

Обработка полученных данных измерений каждого опыта производится по алгоритму прямых измерений с многократным наблюдением.

Рассчитать значение функции  = f(,, )

Вычислить частные производные от функций

, ,

Или, для легко логарифмируемой функции f, от ее логарифма

Вычислить полную погрешность функции

(формула переноса погрешностей) или по эквивалентной формуле для легко логарифмируемой функции

Результаты измерений представляются в форме

 P %, n

6. Обработка данных косвенных измерений выборочным методом

Этот метод применяется в том случае, если совместно измеренные значения аргумента функции xi, yi, zi не образуют выборок, но можно создать выборку значений функции {f}.

По каждому набору совместно измеренных значений аргументов рассчитать значения функции fi = f(xi, yi, zi).

Провести обработку полученной выборки {fi} согласно алгоритму обработки данных прямых измерений, находя среднее значение  и случайную погрешность ∆f функции.

Произвести вывод выражений для частных производных от функции

или для легко логарифмируемой функции f − от ее логарифма

По каждому набору совместно измеренных значений аргументов и погрешности СИ рассчитать погрешность СИ функции

Предполагается, что погрешности СИ измеряемых величин могут быть разными в разных опытах или, если функция имеет удобный для логарифмирования вид, по эквивалентной формуле

где fi − соответствующее данному набору аргументов значение функции.

Вычислить среднюю погрешность СИ функции

Если погрешности СИ аргументов одинаковы во всех опытах или при нахождении максимальных по всей серии опытов значений погрешностей СИ Иx = maxИxi, Иy = maxИyi, Иz = maxИzi, для определения погрешности СИ величины f можно использовать выражение

где , , .

Вычислить полную погрешность функции

Результаты измерений представляются в форме

  P %, n

Методы обработки результатов совместных измерений.

Совместными называют производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. Уравнение совместных измерений имеет вид

yi = f (x1i, x2i, …, xni ; a, b, c, ...), i = 1, 2, ..., n,

где yi, x1i, x2i, ..., xni – значения величин, измеренных одновременно (прямо или косвенно) в i-й измерительной операции; а, b, с, ... – неизвестные искомые величины. Если число уравнений превышает число неизвестных, то эти уравнения в отличие от обычной системы уравнений называют условными. Для решения полученной системы используют метод наименьших квадратов.

Задача нахождения наилучшей аппроксимилирующей кривой в общем случае является достаточно сложной и наиболее просто решается, если функциональная зависимость имеет вид прямой линии y = ax + b. Поэтому на практике, если это возможно, сложные функциональные зависимости сводят к линейным зависимостям. При этом задача нахождения регрессионной кривой сводится к решению следующих задач:

− линеаризация нелинейных зависимостей, которая производится путем соответствующей замены переменных с целью получения новой функции,

− нахождение наилучших значений коэффициентов a и b в линейной зависимости y = ax + b или коэффициента a в линейной зависимости

y = ax согласно методу наименьших квадратов (МНК),

− нахождение случайных погрешностей и погрешностей СИ этих коэффициентов,

− нахождение по найденным значениям коэффициентов a и b физических констант, содержащихся в этих коэффициентах. Последняя задача решается стандартным приемом метода переноса погрешностей при косвенных измерениях.

Метод обработки результатов измерений по методу наименьших квадратов (МНК) для уравнения y = ax + b

Все данные результатов замеров свести в таблицу и произвести обработку этих данных по МНК для уравнения y = ax + b.

Вычислить средние значения x и y

 ,

Определить средние значения … …

,

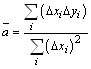Рассчитать дисперсии и СКО

, , ,

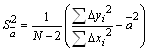Определить случайные погрешности a и b. Для расчета необходимо брать коэффициент Стьюдента tp,n – 1 , в отличие от прямых измерений, где использовался tp,n :

,

Вычислить погрешность СИ коэффициента b (погрешность СИ коэффициента a равна нулю)

Определить полные погрешности a и b

 и

Результаты измерений представляются в форме

, P

Метод обработки результатов измерений по методу наименьших квадратов (МНК) для уравнения y = ax.

Все данные результатов замеров свести в таблицу и провести обработку этих данных по МНК для уравнения y = ax

Вычислить среднее значение a

Вычислить дисперсию и СКО

,

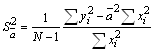Вычислить случайную погрешность коэффициента a

Вычислить погрешность СИ коэффициента a

Вычислить полную погрешность коэффициента a

Результат измерения представляется по форме

, Р

Список использованной литературы

1. ГОСТ Р 8. 563 – 96 Государственная система обеспечения единства измерений. Методика выполнения измерений.

2. МИ 1317 – 2001 Государственная система обеспечения единств измерений. При

Результаты и характеристика погрешностей измерений.

3. РМГ 43 – 2001 Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений».

4. Р 50. 2. 038 – 2004 Государственная система обеспечения единства измерений. Измерения прямые однократные. Оценивание погрешности и неопределенности результата измерения.

5 МИ 1552 – 86 Методика выполнения прямых однократных измерений.

6. ГОСТ 8. 207 – 76 Государственная система обеспечения единства измерений.

Прямые измерения с многократными наблюдениями, методы обработки результатов наблюдений.

7. ГОСТ ИСО 5479 – 2002 Государственная система обеспечения единства измерений. Проверка отклонения распределения вероятностей от нормального распределения.

8. МИ 199 – 70 Государственная система обеспечения единства измерений. Методика установления вида математической модели распределения погрешностей.

9. МИ 2083 – 90 СИ Измерения косвенные. Определение результатов измерений и оценивание их погрешностей.

10. ГОСТ Р ИСО 5725 – 4 – 2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений.

11. А.Г.Сергеев, В.Г.Крохин. Метрология: Учеб. пособие для студентов вузов. М.: Логос, 2001. 408 с.

12. И.Ф.Шишкин. Теоретическая метрология. М.: Издательство стандартов, 1991.472 с.

13. И.Ф.Шишкин, В.Н.Яншин. Прикладная метрология. М.: РИЦ "Татьянин день", 1993. 150 с.

14. Артемьев Б.Г., Лукашов Ю.Е. Справочное пособие для специалистов метрологических служб. – М.: ИПК Издательство стандартов, 2004.

15. И.Ф.Шишкин. Основы метрологии, стандартизации и контроля качества. М.: Стандарты, 1988.