Навигация
Спектри і спектральний аналіз
Спектри і спектральний аналіз
1. Спектри: визначення і класифікація
Відповідно формули ряду Фур'є маємо:
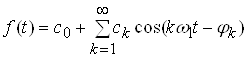 (1)
(1)
Тут ![]() – основна частота. Як бачимо, складна періодична функція
– основна частота. Як бачимо, складна періодична функція ![]() цілком визначається сукупністю величин
цілком визначається сукупністю величин ![]() і
і ![]() . Сукупність величин
. Сукупність величин ![]() зветься спектром амплітуд. Сукупність величин
зветься спектром амплітуд. Сукупність величин ![]() називається відповідно спектром фаз. Для багатьох застосувань досить знати спектр амплітуд; він застосовується настільки часто, що коли говорять про спектр, то мається на увазі саме амплітудний спектр. В інших випадках роблять відповідні застереження. Ми робитимемо так само.
називається відповідно спектром фаз. Для багатьох застосувань досить знати спектр амплітуд; він застосовується настільки часто, що коли говорять про спектр, то мається на увазі саме амплітудний спектр. В інших випадках роблять відповідні застереження. Ми робитимемо так само.
Спектр періодичної функції можна зобразити графічно. Виберемо для цього координати ![]() і
і ![]() .
.
Спектр буде зображений у цій системі координат сукупністю дискретних точок, оскільки кожному значенню ![]() відповідає одне визначене
відповідає одне визначене ![]() . Графік, що складається з окремих точок, незручний. Тому прийнято зображати амплітуди окремих гармонік вертикальними відрізками відповідної довжини.
. Графік, що складається з окремих точок, незручний. Тому прийнято зображати амплітуди окремих гармонік вертикальними відрізками відповідної довжини.
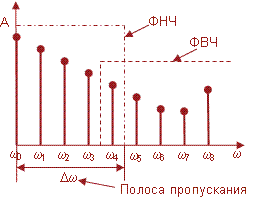
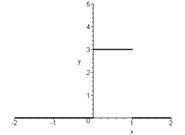
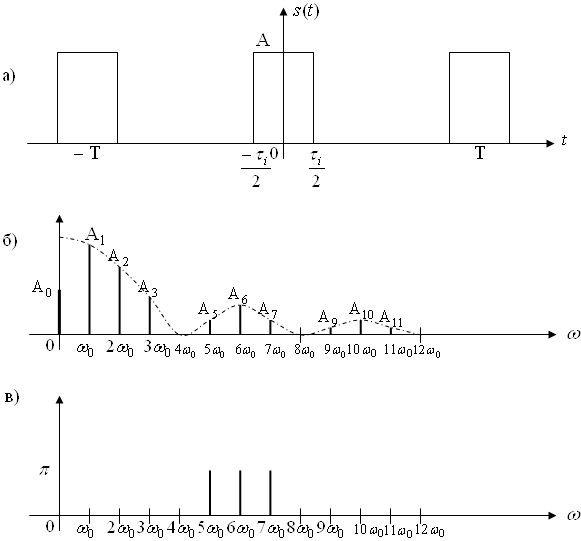
У результаті спектр періодичної функції приймає вигляд, показаний на рис. 1. Це – дискретний спектр; його називають також лінійчастим, запозичивши цей термін з оптики.
Друга властивість спектра, зображеного на рис.1, полягає в тому, що спектр – гармонійний. Це означає, що він складається з рівновіддалених спектральних ліній; частоти гармонік знаходяться в простих кратних співвідношеннях. Зазвичай окремі гармоніки, іноді навіть перша, можуть бути відсутніми, тобто амплітуди їх можуть дорівнювати нулю; це, однак, не порушує гармонійності спектра.
Не слід вважати, що тільки періодична функція має дискретний спектр. Припустимо, наприклад, що складне коливання є результатом додавання двох синусоїдальних коливань з непорівнянними частотами, скажімо, ![]() та
та ![]() . Це коливання свідомо неперіодичне, однак спектр його дискретний і складається з двох спектральних ліній.
. Це коливання свідомо неперіодичне, однак спектр його дискретний і складається з двох спектральних ліній.
Функція, що володіє дискретним спектром з довільно розташованими за частотою спектральними лініями, називається майже періодичною.
Отже, дискретні чи лінійчасті спектри можуть належати як до періодичних, так і до неперіодичних функцій. У першому випадку лінійчастий спектр обов'язково гармонійний.
Велике практичне значення має окремий випадок майже періодичної функції, що подається розкладанням виду
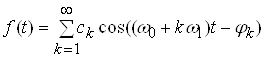 ,
,
де ![]() приймає як позитивні, так і негативні значення. Спектр, що відповідає цьому розкладанню, характеризується тим, що лінії його еквідистантні; тому ми називатимемо такого роду лінійчастий спектр квазігармонійним. Такі, наприклад, спектри періодичних модульованих коливань;
приймає як позитивні, так і негативні значення. Спектр, що відповідає цьому розкладанню, характеризується тим, що лінії його еквідистантні; тому ми називатимемо такого роду лінійчастий спектр квазігармонійним. Такі, наприклад, спектри періодичних модульованих коливань; ![]() у цьому випадку є не що інше, як несуча частота.
у цьому випадку є не що інше, як несуча частота.
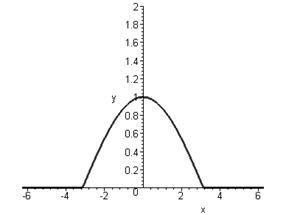
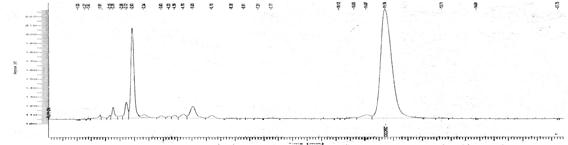
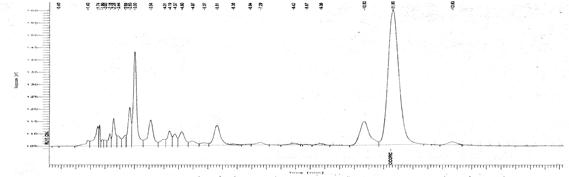
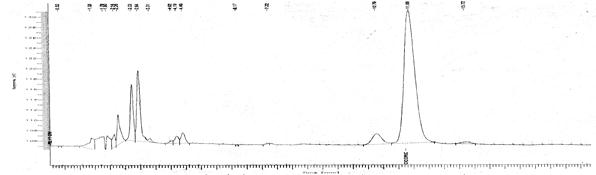
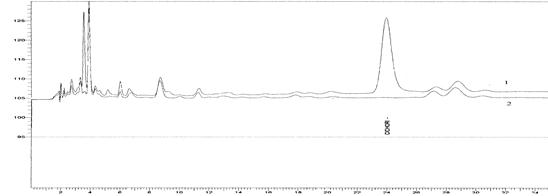
Звернемося тепер до спектрів неперіодичних функцій. Ми вже знаємо, що в результаті граничного переходу від ряду до інтеграла Фур'є інтервали між окремими лініями необмежено скорочуються, лінії зливаються, і замість дискретних точок спектр має зображуватися безперервною послідовністю точок, тобто безперервною кривою. Такого роду спектр називається суцільним. На рис. 2 наведений приклад спектрального розкладання ЕЕГ.
Проте тут потрібно ввести одне уточнення. Ми писали формулу для інтеграла Фур'є у вигляді
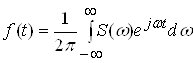 (2)
(2)
Підінтегральна функція виражає окремий нескінченно малий доданок, тобто коливання з нескінченно малою амплітудою ![]() :
:
![]() ,
,
![]() .
.
Таким чином, величина ![]() виражає не безпосередньо амплітуду, а так звану спектральну щільність. Однак зазвичай цю деталь опускають і називають
виражає не безпосередньо амплітуду, а так звану спектральну щільність. Однак зазвичай цю деталь опускають і називають ![]() комплексним спектром неперіодичної функції, а абсолютне значення (модуль) цієї величини
комплексним спектром неперіодичної функції, а абсолютне значення (модуль) цієї величини ![]() – просто спектром. Це може призвести до непорозумінь лише в тому випадку, коли ми безпосередньо порівнюватимемо співвідношення для періодичних і неперіодичних функцій.
– просто спектром. Це може призвести до непорозумінь лише в тому випадку, коли ми безпосередньо порівнюватимемо співвідношення для періодичних і неперіодичних функцій.
Отже, ми маємо два різновиди спектрів: лінійчасті і суцільні. Гармонійні лінійчасті спектри належать періодичним функціям, суцільні – неперіодичним.
Насамкінець зазначимо, що тими чи іншими функціями можуть виражатися зміни різних фізичних величин. Наприклад, спектри механічних величин: зсуву, швидкості, прискорення, сили, тиску тощо; електричних величин: струму, напруги і т.д. Крім того, нас часто цікавлять спектри квадратичних величин: потужності й енергії.
Похожие работы
... координат (наприклад, зображення), у базис деякої періодичної функції. Найбільш часто для спектральної обробки використовується спектр Фур'є, одержуваний на основі базису синуса (розкладання Фур'є, перетворення Фур'є) [7]. Основний зміст перетворення Фур'є в тім, що вихідна неперіодична функція довільної форми, яку неможливо описати аналітично й у загальному випадку важка для обробки й аналізу, ...
... табличні значення відповідних інтегралів: Модуль та аргумент спектральної густини описуємо виразами: (42) (43) Графіки функцій G() та зображені відповідно на рис. 6. Рисунок 6 – Експоненційний імпульс та його спектральні характеристики 4 Спектральна функція детермінованих сигналів Широкого поширення набула комплексна форма представлення спектральних характеристик імпульсних ...
... ії забарвленої речовини і товщини шару розчину визначається об'єднаним законом Бугера-Ламберта-Бера, що є основним законом світлопоглинання і лежить в основі більшості фотометричних методів аналізу: I = I0*10–kCl (3) де k – коефіцієнт светопоглощения, що залежить від природи розчиненої речовини, температури, розчинника і довжини хвилі світла. При дотриманні основного закону светопоглощения ...
... досліджень по дослідженню вмісту біологічно активних речовин, узагальнення результатів, написання тез). Гудзенко А.В. Фармакогностичне дослідження надземної частини кульбаби лікарської (Тaraxacum officinale Wigg.) та розробка способів аналізу біологічно активних речовин. – Рукопис. Дисертація на здобуття наукового ступеня кандидата фармацевтичних наук за спеціальністю 15.00.02 – фармацевтична ...
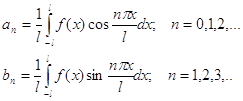
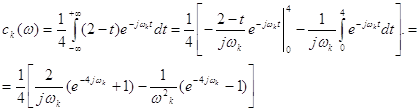





0 комментариев