Навигация
Изохорный процесс. Уравнение изохоры - v = const
3.4.1. Изохорный процесс. Уравнение изохоры - v = const .
Для этого процесса связь между термическими параметрами начального и конечного состояний газа выражается законом Шарля ![]()
![]() .
.
В этом процессе все подводимое тепло расходуется на изменение внутренней энергии, так как газ работы не совершает ![]() , кДж/кг
, кДж/кг
![]() .
.
Изменение энтропии, ![]()
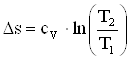 .
.
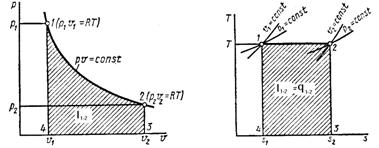
3.4.2. Изобарный процесс. Уравнение изобары - р = const.
Для этого процесса связь между термическими параметрами начального и конечного состояний выражается законом Гей-Люссака ![]() :
:
![]() .
.
Работа изменения объема газа, кДж/кг
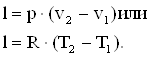
Уравнение первого закона термодинамики для процесса
![]() .
.
В изобарном процессе все подводимое тепло расходуется на изменение энтальпии газа, кДж/кг
![]() .
.
Изменение энтропии, кДж/(кг·К)
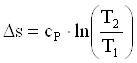 .
.
3.4.3. Изотермический процесс. Уравнение изотермы - ![]() .
.
Для этого процесса справедлив закон Бойля – Мариотта ![]() . Зависимость между начальными и конечными параметрами
. Зависимость между начальными и конечными параметрами
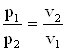 .
.
Работу 1 кг газа можно определить, используя уравнения

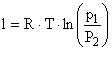 .
.
Внутренняя энергия в изотермическом процессе не изменяется, поэтому
![]() .
.
Количество тепла, сообщаемое газу или отнимаемого от него:
![]() .
.
Изменение энтальпии равно нулю
![]() .
.
Изменение энтропии

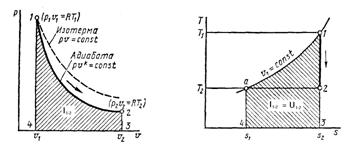
3.4.4. Адиабатный процесс.
Адиабатным называется процесс, протекающий без теплообмена между рабочим телом и окружающей средой ![]() .
.
![]() – уравнение адиабаты, где
– уравнение адиабаты, где ![]() – показатель адиабаты
– показатель адиабаты
 .
.
Зависимость между начальными и конечными параметрами процесса:
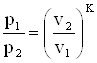 ,
,

Количество теплоты для данного процесса ![]() , тогда уравнение первого закона термодинамики для адиабатного процесса
, тогда уравнение первого закона термодинамики для адиабатного процесса
![]() ,
,
следовательно, изменение внутренней энергии
![]() .
.
Работа расширения совершается из–за убыли внутренней энергии при сжатии же расходуется на повышение внутренней энергии:
![]() или
или
![]() .
.
Изменение энтропии
![]() .
.
3.4.5. Политропный процесс
Политропными называются процессы, в которых теплоемкость имеет любое, но постоянное на протяжении всего процесса значение ![]() .
.
![]() – уравнение политропы, где n – показатель политропы
– уравнение политропы, где n – показатель политропы
 ,
,
где ![]() – теплоемкость политропного процесса,
– теплоемкость политропного процесса, ![]()
 .
.
Зависимость между начальными и конечными параметрами процесса
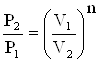 ,
,

Работу в политропном процессе можно определить, используя уравнения:
![]() или
или
![]() ,
,
![]() .
.
Количество теплоты, сообщаемого газу или отнимаемого от него, кДж/кг
![]() .
.
Изменение внутренней энергии
![]() или
или
![]() .
.
Изменение энтропии в политропном процессе
 .
.
В данной работе адиабатный и политропный процессы отсутствуют.
Похожие работы
... термодинамических процессов. Процесс изохорный изобарный изотермический адиабатный 2. Варианты заданий [4] В приведенных ниже вариантах заданий на курсовую работу рассматривается газовые циклы тепловых двигателей. Основное допущение для термодинамического расчета газового цикла теплового двигателя: ...
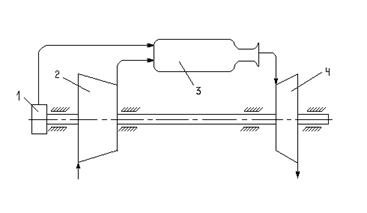
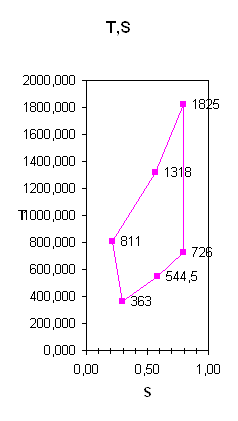
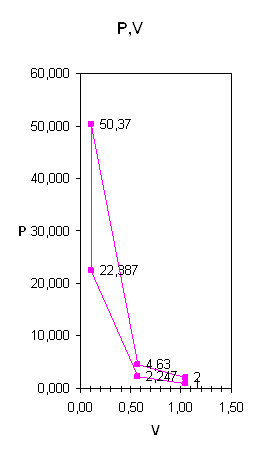
... , определены изменения внутренней энергии, энтальпии, энтропии, теплоты, удельные работы процессов и за цикл. Изображён идеальный цикл в p-v и T-S-координатах. Определены погрешности рассчитанных и . Рассчитаны энергетические характеристики ГТД. Введение Авиационный газотурбинный двигатель является сложной технической системой с высокими удельными параметрами. Конструкция доводилась до ...
... 575 1,725 1,875 ηt % 57,6 59,5 61,2 62,6 63,8 64,9 64,3 63,3 62,4 61,5 60,6 59,7 61,3 61,6 61,8 62,0 62,1 62,2 5.4 Анализ В ДВС с воспламенением рабочей смеси (около ВМТ) от электрической искры время сгорания очень мало, в связи, с чем допустимо принять, что процесс подвода теплоты осуществляется при постоянном объеме ( ...
Исходные данные: Рабочее тело обладает свойствами воздуха, масса равна 1 кг Газовый цикл состоит из четырех процессов, определяемые по показателю политропы. Известны начальные параметры в точке 1 (давление и температура), а также безразмерные отношение параметров в некоторых процессах Дано: n1-2 =1,35; n2-3 = ∞; n3-4 = К; n4-1 = ∞; p1 = 1∙105 Па; t1 = 90 ºC; v1/v2 ...




0 комментариев