Навигация
Розрахунок критичної товщини фазового переходу /111/ГЦК Zr ® /100/ГЩП Zr
2.2 Розрахунок критичної товщини фазового переходу /111/ГЦК Zr ® /100/ГЩП Zr
Зміна умов фазової рівноваги в плівках та частинках малих розмірів може обумовити зміщення температури фазового переходу (високотемпературні фази в масивних зразках стають низькотемпературними в зразках малих розмірів) або виникнення таких поліморфних фаз, які в масивних зразках взагалі не існують. Стисло розглянемо термодинамічну теорію фазового розмірного ефекту.
Якщо в масивному кристалі стійкою є фаза 1, а нерівноважною – фаза 2 (тобто F01 < F02), то для зразка малих розмірів умова термодинамічної стійкості фази 1 записується так:
![]() (2.1)
(2.1)
де V – об’єм зразка.
Це співвідношення записується простіше, якщо розглядати монокристалічні зразки. Для плівки V = A·d, A/V = 2/d, для мікрочастинки сферичної форми V = 4/3πR3. З урахуванням цього, рівняння (2.1) запишеться так [4]:
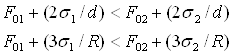 (2.2)
(2.2)
Для того, щоб у зразку малого розміру термодинамічно стійкою була фаза 2, необхідно поміняти знак нерівності:
![]() (2.1')
(2.1')
Можлива така ситуація: співвідношення між s1 та s2 буде таким, що поряд з нерівністю F01 < F02 буде виконуватись нерівність (2.1') завдяки умові s2 < s1. Тоді буде існувати така критична товщина d* (або критичний радіус R*), при якій дві фази будуть в рівновазі [4]:
![]()
![]() (2.3)
(2.3)
При товщинах (радіусах), менших критичної, буде стійкою фаза 2, а при більших - фаза 1, тобто при досягненні критичного розміру відбувається фазовий перехід 2®1. Підкреслимо, що фаза 2 може як спостерігатися в масивних зразках при певних умовах, так і не мати місця ні за яких умов [4].
Якщо розглядати полікристалічний зразок (наприклад, тонку плівку), то рівняння (2.3) перепишеться таким чином [4]:
![]() (2.3’)
(2.3’)
Якщо виконується умова L > d, то ![]() , а
, а ![]() (зауважимо, що L·d ~ площі поверхні кристаліта, 1м2/L2-концентрація кристалітів). Якщо виконується умова
(зауважимо, що L·d ~ площі поверхні кристаліта, 1м2/L2-концентрація кристалітів). Якщо виконується умова ![]() (а це має місце завжди), то можлива ситуація, коли
(а це має місце завжди), то можлива ситуація, коли ![]() або, навіть,
або, навіть, ![]() , коли d·L-1 << 1. Звідси витікає, що оцінку критичної товщини (радіуса) можна здійснювати для випадку монокристалічної плівки [4].
, коли d·L-1 << 1. Звідси витікає, що оцінку критичної товщини (радіуса) можна здійснювати для випадку монокристалічної плівки [4].
Спочатку перетворимо різницю F02 - F01:
![]() (2.4)
(2.4)
де S2 - S1 = l2 —>1/ T0 @ (U2 - U1)/T0; l2 —>1 та T0 - теплота та температура фазо-вого переходу в масивних зразках), e = (U2 - U1) /U1 @ l2 —>1·QB, (QB- теплота випаровування) [4].
Якщо скористатися співвідношеннями для U та s:
![]() ,
,![]() (2.5)
(2.5)
де z0 і zn - об’ємне і поверхневе координаційні числа (число найближчих сусідніх атомів відносно вибраного атома в об'ємі або на поверхні, відповідно);
u - енергія взаємодії двох сусідніх атомів;
n, N - поверхнева та об'ємна концентрація атомів [4].
Після підстановки (2.5) в (2.3) одержуємо вираз для критичної товщини в самому загальному вигляді:
![]() (2.6)
(2.6)
де d = n/N - відстань між атомними шарами, паралельними підкладці [4].
Приведемо розрахунок d* для конкретного фазового переходу (111)ГЦК(2) → (100)ГЩП(1).
Знайдемо усі необхідні параметри для формули 2.6:
1. З умови відомо, що a1 = 0.323 нм.
2. Об’ємне координаційне число z01 та z02 – це число найближчих сусідніх атомів відносно вибраного атома в об’ємі.
Для ГЩК (100) z01 = 12. Для ГЦК (111) z02 = 12.
3. Поверхневе координаційне число zп2 – це число найближчих сусідніх атомів відносно вибраного атома на поверхні.
Для ГЩК (100) zп1 = 6. Для ГЦК (111) zп2 = 6.
4. Відстані між атомними шарами, паралельними підкладці d1 і d2. В загальному випадку d1,2:
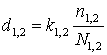 (2.7)
(2.7)
де k1,2 – коефіцієнт пропорційності (в нашому випадку k1 = k2 = 1);
n1,2 – поверхнева концентрація атомів;
N1,2 – об’ємна концентрація атомів.
Знайдемо n1:
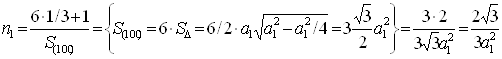 (2.8)
(2.8)
Знайдемо n2. Як видно з рисунка 2.5 n2 буде дорівнювати:
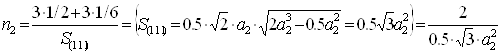 (2.9)
(2.9)
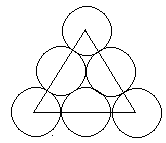
Рисунок 2.5 – Схематичне зображення площини (111) у ГЦК
Знайдемо N1:
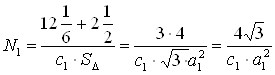 (2.9)
(2.9)
Знайдемо N2. На елементарну ГЦК-комірку припадає 4 атома:
 (2.9)
(2.9)
Теперь найдем d1
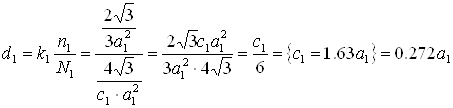 (2.10)
(2.10)
Теперь найдем d2
 (2.11)
(2.11)
Отримавши усі необхідні параметри підставимо їх у формулу (2.6) і отримаємо кінцевий результат:
 (2.12)
(2.12)
Таким чином, критична товщина переходу 111)ГЦК(2) → (100)ГЩП(1) d* дорівнює 12,85 нм, але слід зазначити що значення d* дуже залежить від величини ε.
Висновки
1. Більшість металів у періодичній системі можуть існувати в декількох наступних фазах: кубічна гранецентрована (ГЦК), кубічна об’ємноцентрована (ОЦК) і гексагонально щільно пакована (ГЩП)
2. Структурні перетворення α↔β і α↔ω відбуваються за рахунок невеликих зсувів атомів, пов'язаних, по перше, з наявністю як короткохвильових коливань, визначаючих локальну структуру після переходу, по друге, довгохвильових коливань, що приводять до утворення великомасштабних структур типу двійників.
3. Отримано, що критична фазового переходу /111/ГЦК Zr ® /100/ГЩП Zr, дорівнює 12,85 нм. Також слід зазначити що значення d* дуже залежить від величини ε.
Література
1. Физико-химические свойства элементов: Справочник / Под ред. Г.В. Самсонова. - Киев: Наукова думка, 1965. - 87 с.
2. Физическое металловедение. Вып. ІІ. Фазовые превращения. Металлография / Под ред. Новикова И.И. - Москва: Мир, 1968. - 490 с.
3. Трушицын В.Ю., Долгушева Е.Б., Саламатов Е.И. Моделирование структурной стабильности α-Zr под давленим методом молекулярной динамики // Физика твердого тела.– Т.47, вып. 10.– 2005.– С. 1729-1736.
Похожие работы
... параметрів при термоциклюванні, а саме ця особливість є принциповою для практичного використання. Перспективними для вирішення проблеми деградації об’ємних матеріалів з ФПМН є склокерамічні матеріали на основі компонента з фазовим переходом метал-напівпровідник. Такі матеріали можна отримати за керамічною технологією. Важливою вимогою до них, окрім стабільної поведінки при термоциклюванні, є ...
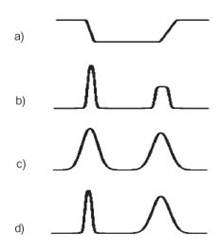
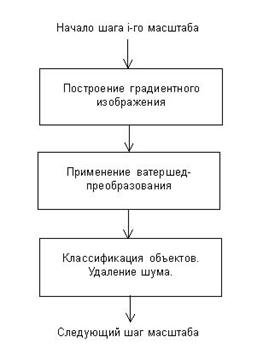
... масштабу. (г) Многомасштабне градієнтное зображення Інші автори дотримуються підходу, при якому остаточна картина границь складається на основі аналізу градієнтних зображень від точних масштабів до не точних. При цьому, основними завданнями при такому підході є зменшення впливу шуму, до якого чутливі оператори градієнта малого розміру, і комбінування границь, отриманих на точних масштабах, із ...
... ів на установці ЭМР-100 у режимі дифракції на відображення з поверхні тертя при напрузі, яка з ковзає , 100 кв. 2.3 Математична модель процесів тертя й зношування покрити по пружно - пластичній основі На підставі [12-21] простір існування властивостей детонаційно-газових покриттів можна описати, як: Ω (Rфм Rмф Rфт Rі) З обліком першого обмеження: Ω Ψ де Ψ - простір ...
... 4 виконавців, тривалість виконання робіт складає 153 днів, ціна теми складає 7. Забезпечення життєдіяльності і питання екології 7.1 Аналіз шкідливих і небезпечних чинників В даній дипломній роботі і досліджений сервопривод урахуванням нелінійності. Основним місцем роботи була науково-виробнича дослідницька лабораторія (НВДЛ) №402, кафедри №301. При проведенні робіт в лабораторіях поді ...




0 комментариев