Теория Бора для атома водорода. Постулаты Бора

6. Теория Бора для атома водорода. Постулаты Бора

Датский физик Нильс Бор (1885–1962) в 1913 г. создал первую квантовую теорию атома, связав в единое целое эмпирические закономерности линейчатых спектров водорода, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света.

В основу своей теории Бор положил три постулата, по поводу которых американский физик Л. Купер заметил: «Конечно, было несколько самонадеянно выдвигать предложения, противоречащие электродинамике Максвелла и механике Ньютона, но Бор был молод».

Первый постулат (постулат стационарных состояний): в атоме электроны могут двигаться только по определенным, так называемым разрешенным, или стационарным, круговым орбитам, на которых они, несмотря на наличие у них ускорения, не излучают электромагнитных волн (поэтому эти орбиты названы стационарными). Электрон на каждой стационарной орбите обладает определенной энергией E_n.

Второй постулат (правило частот): атом излучает или поглощает квант электромагнитной энергии при переходе электрона с одной стационарной орбиты на другую:

hv = E₁ – E₂,

где E₁ и E₂ – энергия электрона соответственно до и после перехода.

При E₁ > E₂ происходит излучение кванта (переход атома из одного состояния с большей энергией в состояние с меньшей энергией, то есть переход электрона с любой дальней на любую ближнюю от ядра орбиту); при E₁ < E₂ – поглощение кванта (переход атома в состояние с большей энергией, то есть переход электрона на более удаленную от ядра орбиту).

Будучи уверенным, что постоянная Планка должна играть основную роль в теории атома, Бор ввел третий постулат (правило квантования): на стационарных орбитах момент импульса электрона L_n= m_eυ_nr_nкратен величине = h/(2π), то есть

m_eυ_nr_n = nh, n = 1, 2, 3, …,

где = 1,05 · 10^-34 Дж · с – постоянная Планка (величина h/(2π)) встречается столь часто, что для нее введено специальное обозначение («аш» с чертой; в данной работе «аш»– прямое); m_е = 9,1 · 10^{-31 кг – масса электрона; r}_п – радиус n-й стационарной орбиты; υ_n – скорость электрона на этой орбите.

7. Атом водорода в квантовой механике

Уравнением движения микрочастицы в различных силовых полях является волновое уравнение Шредингера.

Для стационарных состояний уравнение Шредингера будет таким:

где Δ – оператор Лапласа

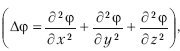
m – масса частицы, h – постоянная Планка, E – полная энергия, U – потенциальная энергия.

Уравнение Шредингера является дифференциальным уравнением второго порядка и имеет решение, которое указывает на то, что в атоме водорода полная энергия должна иметь дискретный характер: ^E1^{, E}2^{, E}3…

Эта энергия находится на соответствующих уровнях n =1,2,3,…по формуле:

Самый нижний уровень E соответствует минимальной возможной энергии. Этот уровень называют основным, все остальные – возбужденными.

По мере роста главного квантового числа n энергетические уровни располагаются теснее, полная энергия уменьшается, и при n = ∞ она равна нулю. При E>0 электрон становится свободным, несвязанным с конкретным ядром, а атом – ионизированным.

Полное описание состояния электрона в атоме, помимо энергии, связано с четырьмя характеристиками, которые называются квантовыми числами. К ним относятся: главное квантовое число п, орбитальное квантовое число l, магнитное квантовое число m₁, магнитное спиновое квантовое число m_s.

Волновая φ-функция, описывающая движение электрона в атоме, представляет собой не одномерную, а пространственную волну, соответствующую трем степеням свободы электрона в пространстве, то есть волновая функция в пространстве характеризуется тремя системами. Каждая из них имеет свои квантовые числа: п, l, m_l.

Каждой микрочастице, в том числе и электрону, также свойственно собственное внутреннее сложное движение. Это движение может характеризоваться четвертым квантовым числом m_s. Поговорим об этом подробнее.

A. Главное квантовое число п, согласно формуле, определяет энергетические уровни электрона в атоме и может принимать значения п = 1, 2, 3…

Б. Орбитальное квантовое число /. Из решения уравнения Шредингера следует, что момент импульса электрона (его механический орбитальный момент) квантуется, то есть принимает дискретные значения, определяемые формулой

где L_l – момент импульса электрона на орбите, l – орбитальное квантовое число, которое при заданном п принимает значение i = 0, 1, 2… (n – 1) и определяет момент импульса электрона в атоме.

B. Магнитное квантовое число m_l. Из решения уравнения Шредингера следует также, что вектор L_l (момент импульса электрона) ориентируется в пространстве под влиянием внешнего магнитного поля. При этом вектор развернется так, что его проекция на направление внешнего магнитного поля будет

L_lz = hm_l

где m_l называется магнитным квантовым числом, которое может принимать значения m_l = 0, ±1, ±2,±1, то есть всего (2l + 1) значений.

Учитывая сказанное, можно сделать заключение о том, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях (n – одно и то же, а l и m_l– разные).

При движении электрона в атоме электрон заметно проявляет волновые свойства. Поэтому квантовая электроника вообще отказывается от классических представлений об электронных орбитах. Речь идет об определении вероятного места нахождения электрона на орбите, то есть местонахождение электрона может быть представлено условным «облаком». Электрон при своем движении как бы «размазан» по всему объему этого «облака». Квантовые числа n и l характеризуют размер и форму электронного «облака», а квантовое число m_l– ориентацию этого «облака» в пространстве.

В 1925 г. американские физики Уленбек и Гаудсмит доказали, что электрон также обладает собственным моментом импульса (спином), хотя мы не считаем электрон сложной микрочастицей. Позднее выяснилось, что спином обладают протоны, нейтроны, фотоны и другие элементарные частицы

Опыты Штерна, Герлаха и других физиков привели к необходимости характеризовать электрон (и микрочастицы вообще) добавочной внутренней степенью свободы. Отсюда для полного описания состояния электрона в атоме необходимо задавать четыре квантовых числа: главное – п, орбитальное – l, магнитное – m_l, магнитное спиновое число – m_s.

В квантовой физике установлено, что так называемая симметрия или асимметрия волновых функций определяется спином частицы. В зависимости от характера симметрии частиц все элементарные частицы и построенные из них атомы и молекулы делятся на два класса. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются асимметричными волновыми функциями и подчиняются статистике Ферми—Дирака. Эти частицы называются фермионами. Частицы с целочисленным спином, в том числе и с нулевым, такие как фотон (Ls =1) или л-мезон (Ls = 0), описываются симметричными волновыми функциями и подчиняются статистике Бозе– Эйнштейна. Эти частицы называются бозонами. Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, также являются фермионами (суммарный спин – полуцелый), а составленные из четного – бозонами (суммарный спин – целочисленный).