Навигация
Обговорення результатів
2.3. Обговорення результатів
При відпалі кристалів PbS у парі сірки змінюється як концентрація, так і вид дефектів (рис.2–5). Так, зокрема, результати теретичного аналізу вказують на те, що збільшення парціального тиску сірки (рис. 2.1), як і зменшення температури відпалу (рис. 3.5), зумовлюють
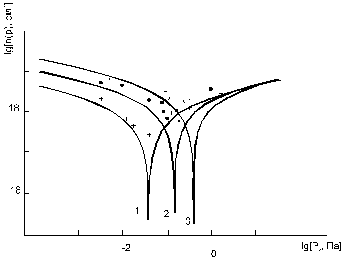
Рис. 2.4. Залежність концентрації носіїв струму PbS від парціального тиску сірки (суцільна лінія- розрахунок згідно (3.3) з використанням знайдених значень констант рівноваги, точки – експеримент) при температурі відпалу Т, К: 1-1000, 2-1100, 3-1200.
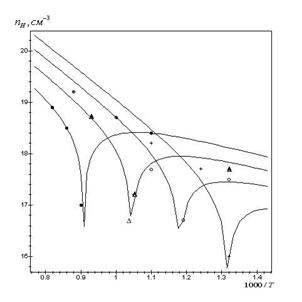
Рис.2.5. Залежність розрахованих згідно (3.3) значень концентрації носіїв струму PbS з використанням знайдених значень констант рівноваги від температури відпалу при парціальному тиску сірки ![]() , Па: 1 - 10-4, 2 - 10-2, 3 - 1.
, Па: 1 - 10-4, 2 - 10-2, 3 - 1.
топологічно ідентичні зміни. Для випадку збільшення парціального тиску сірки спостерігається зменшення концентрації електронів, конверсія провідності з n–на p–тип (термодинамічний n–p–перехід) і подальше зростання концентрації дірок. А у випадку підвищення температури відпалу спочатку відбувається спадання концентрації дірок, аж до моменту настання n–p–переходу, а потім зростання концентрації електронів (рис. 3,5). При цьому в області малих тисків концентрація визначається міжвузловими атомами свинцю (n = ![]() ), а в області високих тисків – концентрацією вакансій свинцю (p =
), а в області високих тисків – концентрацією вакансій свинцю (p = ![]() ) (рис.2.2).
) (рис.2.2).
3.Розрахунок констант рівноваги квазіхімічних реакцій утворення
власних атомних дефектів у халькогенідах свинцю на основі
експериментальних даних про границі області гомогенності
3.1 Квазіхімічне моделювання
Таблиця 3.1Реакції та константи рівноваги К=К0 exp (–DH/kT) утворення переважаючих атомних дефектів у халькогенідах свинцю PbS
| № п/п | Рівняння | Константа рівноваги |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
| |
Припускалося, що в халькогенідах свинцю переважаючим є дефектоутворення у катіоній підгратці за механізмом Френкеля. Згідно [6], процес дефектоутворення в PbS можна описати системою квазіхімічних реакцій (таблиця 3.1). Тут реакція (1) описує утворення пари Френкеля, (2)-(3) – іонізацію утворених дефектів, (4) – збудження власної провідності. Реакція (5) описує проникнення атомів халькогену з парової фази у кристал з утворенням нейтральної ![]() металічної вакансії, а (6) – рівняння повної електронейтральності.
металічної вакансії, а (6) – рівняння повної електронейтральності.
Границі області гомогенності халькогенідів свинцю для надлишку атомів свинцю і халькогену можна розрахувати за формулами[11]:
|
| (3.1) |
де К – константи відповідних квазіхімічних реакцій (див. таблицю 3.1). ![]() – парціальний тиск пари сірки, що відповідає трифазовій рівновазі тверде тіло – рідина – газ в системі свинець - сірка.
– парціальний тиск пари сірки, що відповідає трифазовій рівновазі тверде тіло – рідина – газ в системі свинець - сірка.
Вирази (3.1) дозволяють розрахувати границі області гомогенності якщо відомі константи Ka, Kb, Ki, КF, ![]() . Навпаки, якщо границі області гомогенності відомі з експерименту, то можна визначити константи рівноваги реакцій утворення власних атомних дефектів. Проте, ця задача є досить складною. Для її спрощення константи Ka, Kb, Ki розраховували теоретично, використовуючи зонну теорію невироджених напівпровідників. Константи рівноваги реакцій іонізації дефектів визначали за формулами:
. Навпаки, якщо границі області гомогенності відомі з експерименту, то можна визначити константи рівноваги реакцій утворення власних атомних дефектів. Проте, ця задача є досить складною. Для її спрощення константи Ka, Kb, Ki розраховували теоретично, використовуючи зонну теорію невироджених напівпровідників. Константи рівноваги реакцій іонізації дефектів визначали за формулами:
|
| (3.2) |
|
| (3.3) |
Значення параметрів, які використовувались при розрахунках констант Ka, Kb, Ki [1,2,15]
| Сполука | Носії струму | |
| Eg , еВ | |
| низькі температури | високі темпера-тури | ||||
| PbS | n | 1,3 | 0,160 | 0,275+4,5×10–4Т | 0,45 |
| p | 1,4 | 0,150 | |||
де Еd, Ea - енергії іонізації донорних і акцепторних точкових дефектів, які брали рівними 0,01 еВ. Густини станів в дозволених зонах Nc i Nv можна розрахувати за формулами :
| Nc = 2(2p | (3.4) |
| Nv = 2(2p | (3.5) |
де ![]() ,
, ![]() -ефективна маса електрона в зоні провідності і дірки в валентній зоні відповідно, m0 - маса вільного електрона.
-ефективна маса електрона в зоні провідності і дірки в валентній зоні відповідно, m0 - маса вільного електрона.
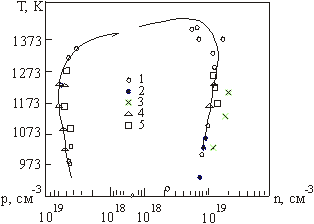
Рис. 3.1. Область гомогенності PbS [2]
Температурну залежність ефективної маси густини станів для електронів і легких дірок визначали за формулою
|
| (3.6) |
де ![]() ; gc = gv = 4
; gc = gv = 4
Вважали, що ефективна маса важких дірок не залежить від температури.
Значення параметрів, які використовувались при розрахунках наведені в таблиці 3.2.
Константу рівноваги реакції збудження власної провідності одержимо з виразу
| Ki = NcNv×exp(–Eg/kT). | (3.7) |
де Eg - ширина забороненої зони.
Таблиця 3.3
Константи рівноваги К = К0 exp (–DH/kT) утворення атомних дефектів у халькогенідах свинцю PbS
| № п/п | Ka | Kb | Ki | KF |
| При-мітка | ||||||||||||||||
| K0, см-3 | DH, еВ | K0, см-3 | DH, еВ | K0, см-6 | DH, еВ | K0, см-6 | DH, еВ | K0, см-6,Па-1/2 | DH, еВ | |||||||||||||
| PbS | ||||||||||||||||||||||
| 1 | 1,4×1021 | 0,14 | 1,4×1021 | 0,14 | 4,8×1041 | 1,0 | 2,1×1042 | 2,5 | 1,5×1016 | 0,50 | [6] | |||||||||||
| 2 | 1,5×1020 | 0,12 | 1,5×1020 | 0,12 | 2,3×1040 | 0,83 | 5,8×1040 | 1,80 | 4,3×1016 | 0,20 | * | |||||||||||
*) – легкі дірки;
**) – важкі дірки.
На відміну від більшості напівпровідників в халькогенідів свинцю ширина забороненої зони в області низьких температур лінійно зростає, а при температурах вищих 500 К лінійність температурної залежності порушується і ширина забороненої зони прямує до сталого значення (таблиця 3.2).
Отримавши таким чином константи Ka, Kb, Ki, значення констант КF, ![]() знайшли апроксимуючи експериментальні залежності границь області гомогенності від температури (рис. 3.1) виразами (3.1). Результати оцінки
знайшли апроксимуючи експериментальні залежності границь області гомогенності від температури (рис. 3.1) виразами (3.1). Результати оцінки ![]() наведені в таблиці 3.3.
наведені в таблиці 3.3.
4. Залежність властивостей плівок ![]() від термодинамічних
від термодинамічних
параметрів
Модель ![]()
Таблиця 4.1.
| № | Реакція | Константа рівноваги |
| I |
|
|
| II |
|
|
| III |
|
|
| IV |
|
|
| V |
|
|
| VI |
| |
|
| (4.1) |
|
| (4.2) |
|
|
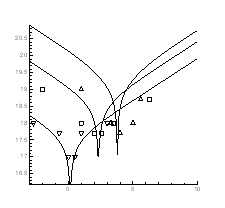
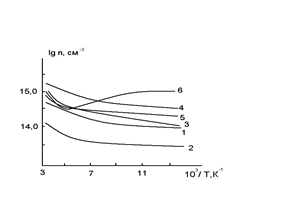
Рис.4.1 Ізотерми концентрації носів заряду ![]() в плівках
в плівках ![]() ,
,![]()
|
|
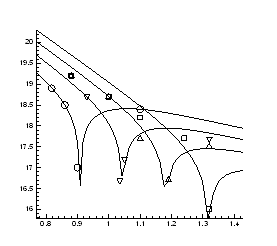
Рис.4.2. Ізобари концентрації носів заряду ![]() в плівках
в плівках ![]() ,
,![]()
|
|
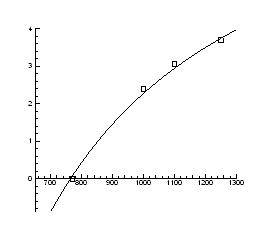
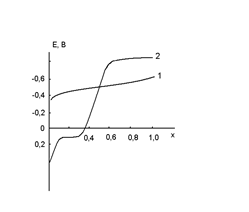
Рис.4.3. Залежність тиску інверсії від температури
|
|
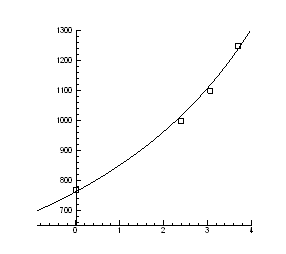
Рис.4.4. Залежність температури інверсії від тиску
|
|
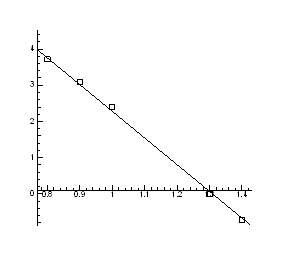
Рис.4.5. P-Т- проекція системи Pb-S
Модель ![]()
Таблиця 4.2.
| № | Реакція | Константа рівноваги |
| I |
|
|
| II |
|
|
| III |
|
|
| IV |
|
|
| V |
|
|
| VI |
|
|
| VII |
| |
|
| (4.3) |
|
|
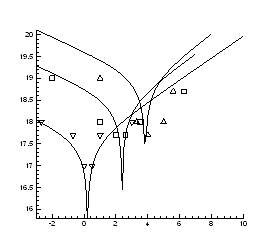
Рис.4.6. Ізотерми концентрації носів заряду ![]() в плівках
в плівках ![]() ,
, ![]()
|
|
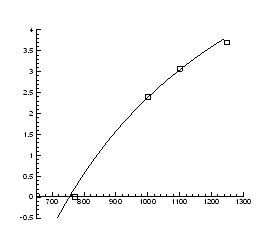
Рис.4.7. Залежність тиску інверсії від температури
|
|
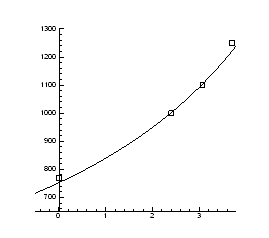
Рис.4.8. Залежність температури інверсії від тиску
|
|
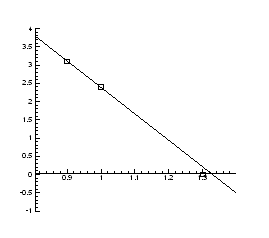
Рис.4.9. P-Т- проекція системи Pb-S
Модель ![]()
Таблиця 4.3.
| № | Реакція | Константа рівноваги |
| I |
|
|
| II |
|
|
| III |
|
|
| IV |
|
|
| V |
|
|
| VI |
|
|
| VII |
| |
|
| (4.4.) |
|
|
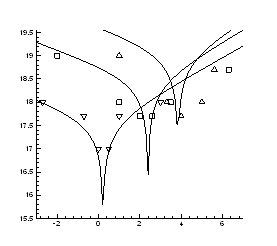
Рис.4.10. Ізотерми концентрації носів заряду ![]() в плівках
в плівках ![]() ,
, ![]()
|
|
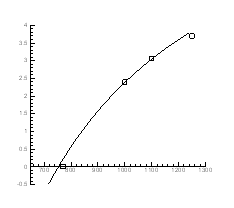
Рис.4.11. Залежність тиску інверсії від температури
|
|
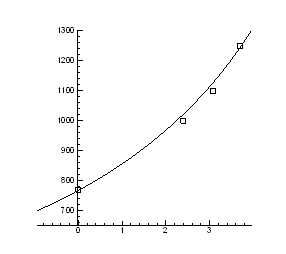
Рис.4.12. Залежність температури інверсії від тиску
|
|
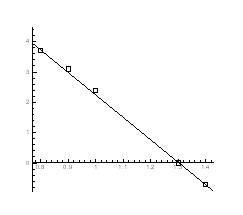
Рис.4.13. P-Т - проекція системи Pb-S
Модель ![]()
Таблиця 4.4.
| № | Реакція | Константа рівноваги |
| I |
|
|
| II |
|
|
| III |
|
|
| IV |
|
|
| V |
|
|
| VI |
|
|
| VII |
|
|
| VIII |
| |
|
| (4.5) |
|
| (4.6) |
|
|
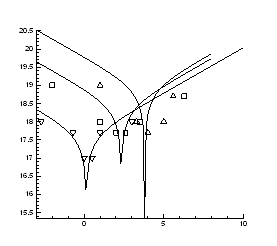
Рис.4.14. Ізотерми концентрації носів заряду ![]() в плівках
в плівках ![]() ,
, ![]()
|
|
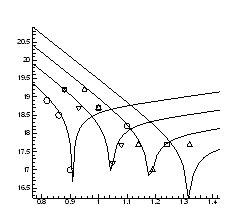
Рис.4.15. Ізобари концентрації носів заряду ![]() в плівках
в плівках ![]() ,
,![]()
|
|
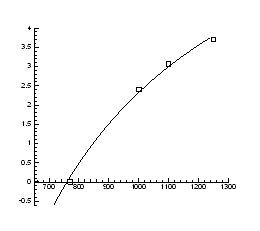
Рис.4.16. Залежність тиску інверсії від температури
|
|
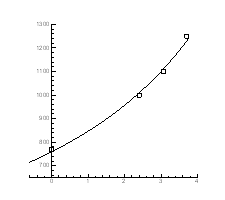
Рис.4.17. Залежність температури інверсії від тиску
|
|
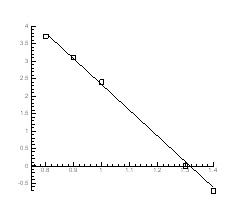
Рис.4.18. P-Т - проекція системи Pb-S
Модель ![]()
Таблиця 4.5.
| № | Реакція | Константа рівноваги |
| I |
|
|
| II |
|
|
| III |
|
|
| IV |
|
|
| V |
|
|
| VI |
|
|
| VII |
|
|
| VIII |
| |
|
| (4.7) |
|
| (4.8) |
|
|
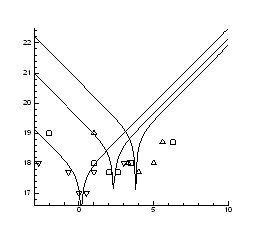
Рис.4.19. Ізотерми концентрації носів заряду ![]() в плівках
в плівках ![]() ,
, ![]()
|
|
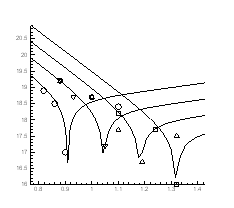
Рис.4.20. Ізобари концентрації носів заряду ![]() в плівках
в плівках ![]() ,
,![]()
|
|
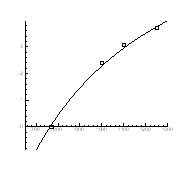
Рис.4.21. Залежність тиску інверсії від температури
|
|
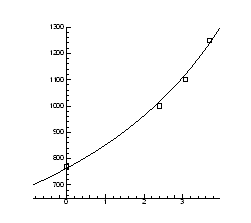
Рис.4.22. Залежність температури інверсії від тиску
|
|
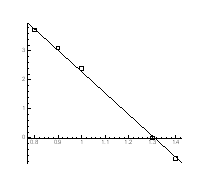
Рис.4.23. P-Т - проекція системи Pb-S
Таблиця 4.6.
| № | Реакція | Константа рівноваги | Теоретичні | Розраховані | ||
|
|
|
|
| |||
| I |
|
|
|
|
|
|
| II |
|
|
|
|
|
|
| III |
|
|
|
|
|
|
| IV |
|
|
|
|
|
|
| V |
|
|
|
|
|
|
| VI |
|
|
|
|
|
|
| VII |
|
|
|
|
|
|
Література:
[1] Ю.М.Равич, Б.А.Ефимова, Н.А.Смирнов, Методы исследования полупроводников в применении к халькогенидам свинца PbTe, PbSe, PbS, Наука, М. (1968)
[2] Н.Х.Абрикосов, Л.Е.Шалимова. Полупроводниковые материалы на основе соединений АIVВVI. Наука, М. (1975).
[3] И.М.Раренко, Д.М. Фреик. Полупроводниковые материалы и приборы инфракрасной техники. ЧДУ, Черновцы (1980).
[4] Ф.Ф.Сизов. Твердые растворы халькогенидов свинца и олова и фотоприемники на их основе // Зарубеж. электрон. техника, 24, сс.3-48 (1977).
[5] H.Holloway. Thin Films IV-VI semiconductor photodiodes // Phys. Thin Films, 11, pp.105-203 (1980).
[6] Ф.Крегер, Химия несовершенных кристаллов, Мир, М. (1969).
[7] В.П.Зломанов, О.В.Матвеев, А.В.Новоселова. Физико-химическое исследование селенида свинца // Вестник МГУ. Химия, 5, cc.81-89 (1967).
[8] В.П.Зломанов, О.В.Матвеев, А.В.Новоселова. Определение констант равновесий дефектов в селениде свинца // Вестник МГУ. Химия, 6, cc.67-71 (1968).
[9] А.В.Новоселова, В.П.Зломанов. Физико-химическое исследование селенида свинца // Неорган. материалы, 3(8), cc.1323-1329 (1967).
[10] А.М.Гаськов, О.В.Матвеев, В.П.Зломанов, А.В.Новоселова. Исследование теллурида свинца // Неорган. материалы. 4(11), cc. 1889-1894 (1969)
[11] А.М.Гаськов, В.П.Зломанов, А.В.Новоселова. Область гомогенности теллурида свинца // Неорган. материалы. 15(8), cc.1476-1478 (1979)
[12] В.П.Зломанов, А.М.Гаськов. Собственные и примесные дефекты в соединениях группы AIVBVI // Рост полупроводниковых кристаллов и плёнок: новые методики, критерии функциональной пригодности материалов, Новосибирск, сс.116-133 (1984).
[13] В.П.Зломанов. P-T-x-диаграммы двухкомпонентных систем. МГУ, М. (1980).
[14] В.П.Зломанов, А.В.Новоселова. Р-Т-х-диаграммы состояния системы металл-халькоген. Наука, М. (1987).
[15] Е.Д. Девяткова, В.А.Саакян. Температурная зависимость ширины запрещенной зоны твердых растворов PbTexSe1-x // ФТТ. 10(5), сс. 1563–1565 (1968).
np
restart:with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> for T from 700 to 1300 by 25 do
> ka:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(2.2e16*exp((-0.52)/((1.380662e-23/1.60219e-19)*T)));
> n:=ki^(1/2);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> P:=solve(Q,p);
> Data:=[op(Data),[evalf(1000/T),evalf(log10(P))]];
> od:
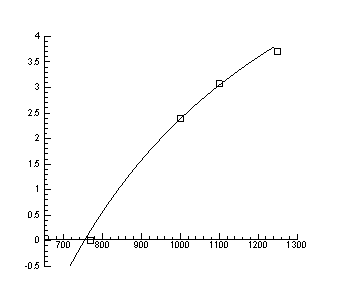
> Data1:=[[1.4,-5/7], [0.8,3+5/7], [0.9,3.1], [0.9,3.1], [1,2.4], [1.3,0]];
> A:=plot(Data1, style=point,symbol=circle,color=black):
> B:=plot(Data,x=0.7..1.5,y=-2..4):
> display(A,B);
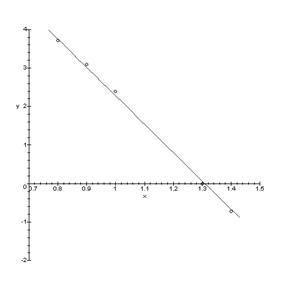
константа
> restart:
> with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> T:=1250;
> ka:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(1.63e27*exp((-0.2)/((1.380662e-23/1.60219e-19)*T)));
> n:=0.75*10^18;
> p:=10^(4);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> P:=solve(Q,kt);
> plot(Data):
> plot(f(x),x=0..1):
> Q:=n+n*kb/ki*kt*p^(-1/2)=ki/n+ka/n*kf/kt*p^(1/2);
> ln(2.041*10^9);
> with(stats):
> fit[leastsquare[[x,y], y=a/x+b, {a,b}]]([[770,1250],[21.436,39.055]]);
> evalf(exp(67.3188));
> k:=(1.380662e-23/1.60219e-19);
> 35329.7*k;
Nx(p) T=const
> restart:
> with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> z:=100;
> v1:=1;
> v:=5;
> T:=770;
> for p1 from -3 to 10 by 0.1 do
> ka:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(v1*4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(z*2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(z^(1/2)*2.2e16*exp((-0.525)/((1.380662e-23/1.60219e-19)*T)));
> p:=10^(p1);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> N:=solve(Q,n)[2];
> Nx:=abs(N-ki/N);
> G:=N*kb/ki*kt*p^(1/2);
> Data:=[op(Data),[(p1),evalf(log10(Nx))]];
> od:
> DataE:=[[3,18],[-2.7,18],[1,17.7],[-0.7,17.7], [0,17], [0.5,17]];
> A:=plot(Data):
> B:=plot(DataE, style=point,symbol=circle):
> display(A,B);
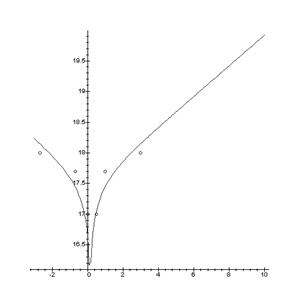
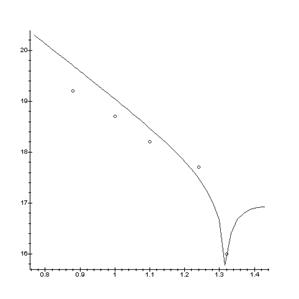
Nx(T) P= const
> restart:
> with(plots):
> Data1:=[]:
> Data:=[]:
> Ki:=ko(-h/kT);
> z:=100;
> v1:=1;
> v:=5;
> p1:=0:
> for T from 700 to 1300 by 10 do
> ka:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(v*1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(v1*4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(z*2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(z^(1/2)*2.2e16*exp((-0.525)/((1.380662e-23/1.60219e-19)*T)));
> p:=10^(p1);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> N:=solve(Q,n)[2];
> Nx:=abs(N-ki/N);
> G:=N*kb/ki*kt*p^(1/2);
> Data:=[op(Data),[(1000/T),evalf(log10(Nx))]];
> od:
> DataE:=[[0.88,19.2], [1.0,18.7], [1.1,18.2], [1.24,17.7], [1.32,16]];
> A:=plot(Data):
> B:=plot(DataE, style=point,symbol=circle):
> display(A,B);
restart:with(plots):
> Data:=[]:
> Ki:=ko(-h/kT);
> for T from 700 to 1300 by 25 do
> ka:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> kb:=evalf(1.4e21*exp((-0.14)/((1.380662e-23/1.60219e-19)*T)));
> ki:=evalf(4.8e41*exp((-1.00)/((1.380662e-23/1.60219e-19)*T)));
> kf:=evalf(2.1e42*exp((-2.5)/((1.380662e-23/1.60219e-19)*T)));
> kt:=evalf(2.2e16*exp((-0.52)/((1.380662e-23/1.60219e-19)*T)));
> n:=ki^(1/2);
> Q:=n+n*kb/ki*kt*p^(1/2)=ki/n+ka/n*kf/kt*p^(-1/2);
> P:=solve(Q,p);
> Data:= [op(Data),[evalf(1000/T),evalf(log10(P))]];
> Data1:= [op(Data),[T),evalf(log10(P))]];
od:
> Data3:=[[1.4,-5/7], [0.8,3+5/7], [0.9,3.1], [0.9,3.1], [1,2.4], [1.3,0]];
> A:=plot(Data):
> B:=plot(Data1):
> C:=plot(Data2):
> display(A,C);
> display(B,C);
|
|
|
|
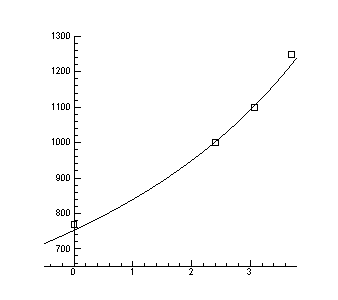
Похожие работы
... заряджені дефекти впливають також на матричні елементи для переходів між нелокалізованими станами поблизу країв рухливості, створюючи флуктуації потенціалу. РОЗДІЛ 2 ФОТОІНДУКОВАНІ ЗМІНИ ОПТИЧНИХ ПАРАМЕТРІВ ТОНКИХ ШАРІВ НЕКРИСТАЛІЧНИХ ХАЛЬКОГЕНІДІВ 2.1. Структурні одиниці та фізико-хіміні особливості некристалічних халькогенідів Структура склоподібних і аморфних халькогенідів може бути ...
... шаром гасу чи вазелинового масла. При внесенні у вогонь деякі лужноземельні метали дають характерне забарвлення: кальцій - темно-оранжеве, барій та радій - темно-червоне, стронцій - блідо-зелене. 2.2.3 Хімічні властивості Метали ІІА-підгрупи мають загальну електронну формулу зовнішнього енергетичного рівня ns2, на попередньому електронному шарі містять по всім електронів, а атом берилію - ті ...
... відповідності із структурними характеристиками, гратки- "господарі" схематично можна розділити на три різні групи одновимірні, що містять структурні елементи ланцюгового типу; двовимірні, утворені структурними елементами шаруватої матриці(гостьові позиції знаходяться в енергетичній щілині ван-дер-ваальса, розташованій між сусідніми шарами); тривимірні - 3^, з сотовою матрицею. У випадку одно - і ...
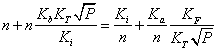
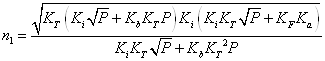
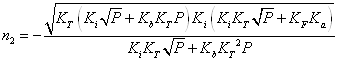
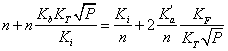
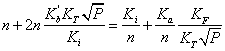
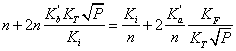
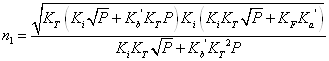
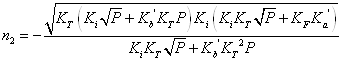
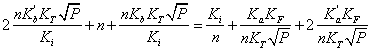



0 комментариев