Навигация
Межрегиональный центр переподготовки специалистов
ЭКЗАМЕНАЦИОННАЯ РАБОТАпо дисциплине
«Электромагнитные поля и волны»
Выполнил:Проверил:
Лиманский В.Н.
Новосибирск, 2010
Излучение электромагнитных волн. Электродинамические потенциалы. Элементарный электрический излучатель. Поля излучателя в ближней и дальней зонах.
Возможность излучения электромагнитных волн, т.е. передачи электромагнитной энергии из некоторой замкнутой области, содержащей сторонние источники, в окружающее пространство, непосредственно вытекает из уравнения баланса электромагнитной энергии. Излучение электромагнитных волн может иметь место только при переменных токах. Экспериментальное подтверждение возможности излучения электромагнитных волн впервые осуществлено опытами Г.Герца. Определяющее значение в использовании этой возможности для практической деятельности человека и, следовательно, для становления современной радиотехники, имело изобретение радио А.С.Поповым в 1895г.
Сформулируем задачу: пусть в среде, характеризуемой параметрами eа, mа и sраспределен сторонний ток jст. Требуется определить векторы ![]() и
и ![]() , удовлетворяющие уравнениям Максвелла (3.2[4]).
, удовлетворяющие уравнениям Максвелла (3.2[4]).
Для определения векторов поля по заданным источникам обычно применяют искусственный прием: сначала находят вспомогательные функции, а потом через них уже вычисляют векторы ![]() и
и ![]() . Эти вспомогательные функции принято называть электродинамическими потенциалами.
. Эти вспомогательные функции принято называть электродинамическими потенциалами.
Выпишем уравнения Максвелла в комплексной форме с учетом сторонних сил и введем вспомогательные функции.
 (4.1[4])
(4.1[4])
Используя материальные уравнения, преобразуем первое уравнение Максвелла следующим образом:
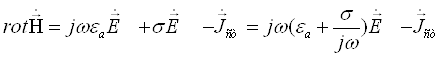 .
.
Или окончательно:
![]() ,
,
где: 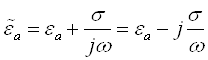 - называется комплексной диэлектрической проницаемостью среды.
- называется комплексной диэлектрической проницаемостью среды.
Для хороших диэлектриков, например воздуха, s » 0 и, соответственно, ![]() .
.
Введем вспомогательную функцию, которую впредь будем называть векторным электродинамическим потенциалом ![]() , следующим образом:
, следующим образом:
![]() (4.2[4])
(4.2[4])
Отсюда:
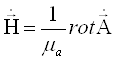 . (4.3[4])
. (4.3[4])
Подставим (4.2[4]) во второе уравнение Максвелла:
![]() ,
,
отсюда:
![]() . (4.4[4])
. (4.4[4])
Из курса высшей математики известно:
![]() ,
,
где ![]() - некоторая скалярная величина.
- некоторая скалярная величина.
Пользуясь этим, введем еще одну вспомогательную функцию – скалярный электродинамический потенциал ![]()
![]() (4.5[4])
(4.5[4])
Тогда из этого выражения получаем:
![]() . (4.6[4])
. (4.6[4])
Используя материальные уравнения и выражения (4.3[4]), определяем вектор электрической индукции:
![]() (4.7[4])
(4.7[4])
Таким образом, все векторы, характеризующие электромагнитное поле (![]() и
и ![]() ), выражаются через две вспомогательные функции:
), выражаются через две вспомогательные функции:![]() . Следовательно, теперь задача состоит в том, чтобы определить эти две функции. Для этого подставим (4.3[4]) и (4.6[4]) в первое уравнение Максвелла.
. Следовательно, теперь задача состоит в том, чтобы определить эти две функции. Для этого подставим (4.3[4]) и (4.6[4]) в первое уравнение Максвелла.
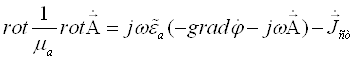 ,
,
![]() .
.
Учитывая известное из высшей математики тождество ![]() , где
, где ![]() - любая векторная величина, преобразуем полученное выражение следующим образом:
- любая векторная величина, преобразуем полученное выражение следующим образом:
![]() .
.
![]() .
.
Поскольку ![]() - произвольные вспомогательные функции, то зададим их таким образом, чтобы выполнялось условие:
- произвольные вспомогательные функции, то зададим их таким образом, чтобы выполнялось условие:
![]() . (4.8[4])
. (4.8[4])
Условие (4.8[4]) получило название условие калибровки Лоренца.
С учетом (4.8[4]) окончательно получаем:
![]() , (4.9[4])
, (4.9[4])
где: ![]() – называют волновым числом,
– называют волновым числом,
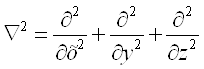 – оператор Лапласа.
– оператор Лапласа.
Аналогичным образом, подставляя в третье уравнение Максвелла уравнение (4.7[4]), затем, учитывая условие калибровки Лоренца и известное тождество ![]() , где
, где ![]() – некая скалярная величина, после несложных преобразований получим:
– некая скалярная величина, после несложных преобразований получим:
![]() . (4.10[4])
. (4.10[4])
Таким образом, мы получили два неоднородных дифференциальных уравнения второго порядка для функций ![]() . Среди множества решений выбирается то, которое удовлетворяет условию калибровки (4.8[4]), и затем уже с помощью (4.2, 4.3, 4.6, 4.7 [4]) определяются векторы электромагнитного поля.
. Среди множества решений выбирается то, которое удовлетворяет условию калибровки (4.8[4]), и затем уже с помощью (4.2, 4.3, 4.6, 4.7 [4]) определяются векторы электромагнитного поля.
Опуская ввиду громоздкости строгий вывод решения неоднородных дифференциальных уравнений (4.9[4]) и (4.10[4]), приведем лишь конечный результат решения этих уравнений:
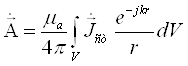 , (4.11[4])
, (4.11[4])
![]() , (4.12[4])
, (4.12[4])
где: V – область пространства, содержащая сторонние источники;
r – расстояние от источника до точки наблюдения (см. рис.1).
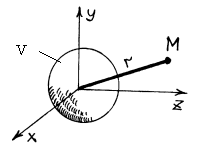
Рис.1. К пояснению выражений для электродинамических потенциалов
Рассмотрим простейший излучатель электромагнитных волн в виде короткого отрезка провода. Дадим определение:
Элементарным электрическим излучателем (ток Iст вибратором) называют отрезок провода, вдоль которого течет переменный ток с постоянной амплитудой Iстm = const, причем длина l этого проводника значительно меньше излучаемой длины волны l.
Представим ток Iств комплексной форме:
![]() .
.
Применим к отрезку провода, по которому протекает ток Iст, закон сохранения заряда (см. ур. 1.26[4])
![]() ,
,
или:Iстm = –jwQm, т.е. амплитуда изменения заряда в проводе пропорциональна изменению в нем амплитуды тока. Поскольку, по условию, амплитуда тока вдоль провода постоянна, то изменение будет происходить лишь на концах этого провода. Следовательно, элементарный электрический вибратор по своей сути представляет электрический колеблющийся диполь (см.рис.2).
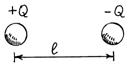
Рис. 2. Эквивалентность элементарного электрического излучателя и колеблющегося диполя
Малость длины l излучателя по сравнению с длиной волны l позволяет рассматривать его как точечный источник электромагнитных волн. Отметим, что первый искусственный излучатель, который использовал в своих опытах Герц, представлял собой два металлических шара, перезаряжаемых с высокой частотой индукционной катушкой (см. рис.3), т.е. являлся ничем иным, как колеблющимся диполем. Данный излучатель получил название диполя Герца.
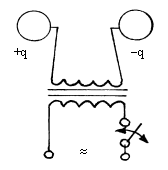
Рис.3. Диполь Герца
Перейдем теперь к анализу элементарного электрического вибратора. Определим векторы напряженности электрического и магнитного полей ![]() при заданном источнике сторонних сил
при заданном источнике сторонних сил ![]() . Для этого вычислим вначале вспомога-тельную функцию – векторный электродинами-ческий потенциал
. Для этого вычислим вначале вспомога-тельную функцию – векторный электродинами-ческий потенциал ![]() , используя (4.11[4]):
, используя (4.11[4]):
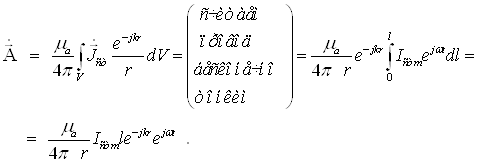 (4.13[4])
(4.13[4])
Расположим элементарный электрический вибратор в сферической системе координат (см. рис.4). Теперь с помощью (4.3[4]) определим напряженность магнитного поля электрического излучателя:
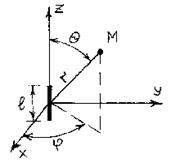
Рис. 4. Расположение вибратора в сферической системе координат
· Из векторной математики. Операция rot в сферической системе координат некой векторной величины ![]() :
:

где:![]() – единичные векторы
– единичные векторы
![]()
Вычисление операции rot проводим в сферической системе координат. Обратив внимание в (4.13[4]) на то, что ![]() зависит только от r (и не зависит от j и q), в результате получим:
зависит только от r (и не зависит от j и q), в результате получим:
 (4.14[4])
(4.14[4])
Величину напряженности электрического поля вне области, содержащей источники сто-ронних сил, проще всего определить из первого уравнения Максвелла (причем будем полагать, что среда в этой области хороший диэлектрик, s » 0):
![]() ,
,
отсюда: ![]() . Раскрывая операцию rot в сферической системе координат, получим:
. Раскрывая операцию rot в сферической системе координат, получим:
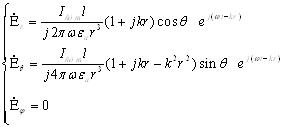 (4.15[4])
(4.15[4])
Из полученных уравнений (4.14[4]) и (4.15[4]) несложно заметить, что составляющие электромагнитного поля электрического излучателя зависят от расстояния r. Вследствие этого принято различать ближнюю и дальнюю зоны излучателя.
Рассмотрим поле в ближней зоне:
Этот случай характеризуется тем, что расстояние r от излучателя значительно меньше длины излучаемой волны l, т.е. r << l.
Поскольку:
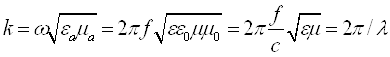 ,
,
где: ![]() – скорость света;
– скорость света;
e, m – относительная диэлектрическая и магнитная проницаемости воздуха (равные единице),
то условие r << l означает что:
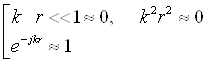
Тогда из (4.14[4]) и (4.15[4]) получаем следующие комплексные значения составляющих электромагнитного поля в ближней зоне:
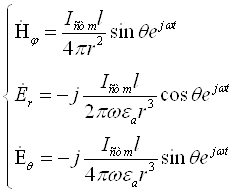 (4.16[4])
(4.16[4])
Перейдем от комплексных значений к мгновенным, (т.е. возьмем вещественную часть от приведенных выражений)
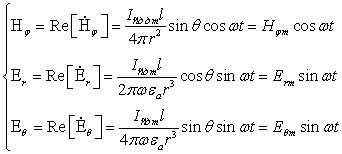 (4.17[4])
(4.17[4])
На основании (4.17[4]) можно отметить следующие основные свойства электромагнитного поля элементарного электрического излучателя в ближней зоне:
1. Составляющие электромагнитного поля убывают в зависимости от расстояния r по разному: амплитуда электрического поля по закону 1/r3, амплитуда магнитного – по закону 1/r2.
2. Поскольку sin(wt) = cos(wt - p/2), то это означает, что электрическое и магнитное поля сдвинуты во времени по фазе на 900.
3. Определим вектор Пойнтинга в ближней зоне (т.е. плотность потока мощности, выходящего сквозь замкнутую поверхность S вокруг вибратора). Из (4.17[4]) следует, что вектор Пойнтинга будет иметь две составляющие:
![]() и
и ![]() .
.
Мгновенные значения:
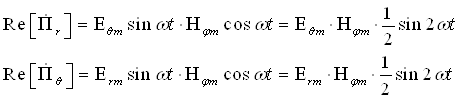
Отсюда видно, что обе составляющие вектора Пойнтинга изменяются во времени по закону sin(2wt) , т.е. принимает как положительные, так и отрицательные мгновенные значения. Очевидно, что среднее значение составляющих вектора ![]() за период колебаний Т будет равно нулю. Это означает, что движение энергии ближнего поля имеет колебательный характер – в течение четверти периода Т (поскольку 2w) энергия движется в одном направлении, в течение следующей четверти периода энергия движется в противоположном направлении.
за период колебаний Т будет равно нулю. Это означает, что движение энергии ближнего поля имеет колебательный характер – в течение четверти периода Т (поскольку 2w) энергия движется в одном направлении, в течение следующей четверти периода энергия движется в противоположном направлении.
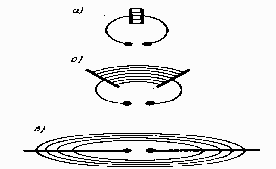
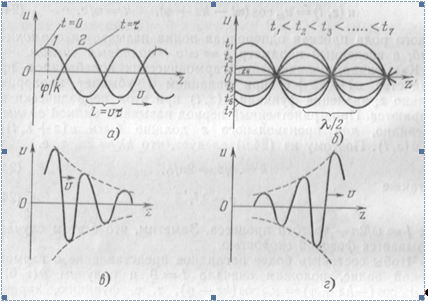
Вывод: Таким образом, ближнее электромагнитное поле не участвует в процессе излучения и имеет характер квазистационарного поля. Поясним сказанное рис.5 на примере струны, закрепленной на бесконечности.
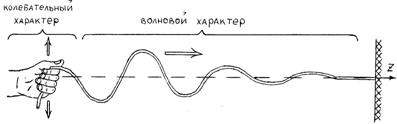
Рис.5 Пример, поясняющий характер процесса в "ближней" и "дальней" зоне. Видно, что относительно распространения волны (ось z) в "ближней" зоне преобладает колебательный характер, тогда как в " дальней" зоне – волновой характер
Ближнюю зону называют также зоной индукции.
Рассмотрим теперь поле в дальней зоне. Этот случай характеризуется тем, что r >> l, и соответственно, kr >> 1. Используя это, можно записать:
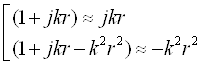
Тогда из (4.14[4]) и (4.15[4]) получаем следующие комплексные значения составляющих электромагнитного поля в дальней зоне:
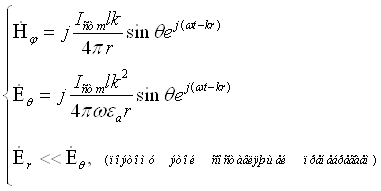 (4.18[4])
(4.18[4])
Перейдем от комплексных значений к мгновенным:
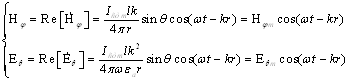 (4.19[4])
(4.19[4])
Исходя из (4.19[4]) отметим следующие основные свойства электромагнитного поля элементарного электрического излучателя в дальней зоне:
Похожие работы
... и магнитные потоки. «... в бегущей плоской электромагнитной волне электрическая энергия в любой момент равна магнитной.» Общий курс физики. Электричество. Д.В.Сивухин. 1996. Т.3. Ч.2. С.18. Например, в дискретной электромагнитной волне - фотоне энергия электрического потока равна энергии магнитного потока: Wэ = Wм = eФ0v, т.е. электромагнитная энергия фотона: W = Wэ + Wм = 2eФ0v. Если E = ...
... переменного тока проводимости или тока смещения, где длина волны зависит от частоты колебания. Любой электрический ток, согласно электродинамике, всегда замкнут. Поэтому продольные электромагнитные волны всегда замкнуты независимо от того, представляют они переменный электрический ток проводимости или смещения. Продольные электрические возмущения поля имеют продольную ориентацию электрического ...
... переходит в энергию вылетевших электронов. Остальная часть поглощенных световых квантов ведет к нагреванию металлов. Шкала электромагнитных волн Электромагнитные излучения с различными длинами волн имеют довольно много различий, но все они, от радиоволн и да гамма-излучения, одной физической природы. Все виды электромагнитного излучения в большей или меньшей степени проявляют свойства ...
... , хотя изучение поведения бегущих волн в замкнутых системах представляет и чисто практический интерес. В настоящей работе проведено экспериментальное исследование поведения бегущих электромагнитных волн в волноводном тракте. Целью настоящей работы являлось исследование частотной зависимости амплитуды бегущей электромагнитной волны в кольцевом волноводном тракте. Для этого необходимо было решить ...

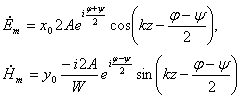
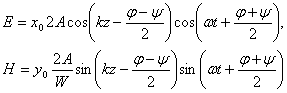
0 комментариев