Навигация
Определим фазовую постоянную
1. Определим фазовую постоянную.
Для начала, найдем тангенс угла потерь:
 ;(2.12 [2]), где
;(2.12 [2]), где
![]() удельная проводимость среды;
удельная проводимость среды;
![]() круговая частота гармонических колебаний;
круговая частота гармонических колебаний;
![]() абсолютная диэлектрическая проницаемость среды.
абсолютная диэлектрическая проницаемость среды.
Круговая частота гармонических колебаний равна:
![]() рад/с. (стр.30[1]), где
рад/с. (стр.30[1]), где
![]() частота плоской электромагнитной волны.
частота плоской электромагнитной волны.
Абсолютная диэлектрическая проницаемость среды равна:
![]() Ф/м. (1.36[2]) ,
Ф/м. (1.36[2]) ,
где
![]() электрическая постоянная, равная:
электрическая постоянная, равная:
![]() Ф/м. (1.11[3]).
Ф/м. (1.11[3]).
Подставив числовые значения в (2.12 [2]), вычислим ![]() :
:
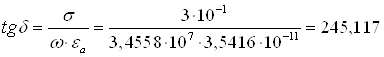
Далее, определим фазовую постоянную по формуле:
![]() ; (6.7 [1]), где
; (6.7 [1]), где
![]() абсолютная магнитная проницаемость среды.
абсолютная магнитная проницаемость среды.
Относительная магнитная проницаемость всех диамагнитных и большинства парамагнитных веществ весьма мало отличается от единицы, поэтому в расчетах данной задачи эффектами диа- и парамагнетизма пренебрежем, считая, что ![]() . Отсюда:
. Отсюда:
![]() Гн/м. (1.63[3]).
Гн/м. (1.63[3]).
Подставив числовые значения в (6.7 [1]), получим:
![]()
2. Определим длину волны в среде.
Так как ![]() , то потери происходят как в проводящих средах, соответветственно длина волны определяется по формуле:
, то потери происходят как в проводящих средах, соответветственно длина волны определяется по формуле:
 ; (6.28[1])
; (6.28[1])
Подставив числовые значения в (6.28[1]), получим:
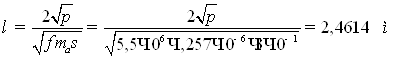
3. Определим расстояние, на котором длина волны убывает на 100 дБ.

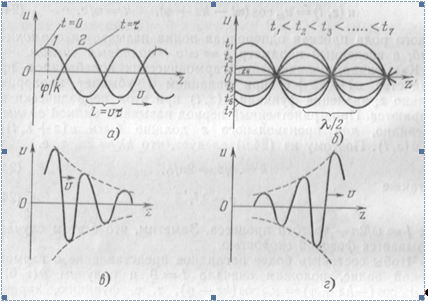
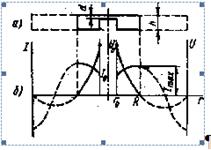
Рис.10 Уменьшение амплитуды плоской волны при распространениии в среде с потерями.
Расстояние Z, на котором амплитуда волны убывает (затухает) на 100 дБ, найдем, используя закон изменения амплитуды вдоль оси распространения, который можно записать как:
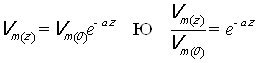 ; (3.8[2]), где
; (3.8[2]), где
![]() коэффициент ослабления плоской волны в среде, равный:
коэффициент ослабления плоской волны в среде, равный:
![]() ; (6.8 [1])
; (6.8 [1])
Подставив числовые значения в (6.8 [1]), получим:
![]()
Так как амплитуда затухает на 100 дБ, то отношение 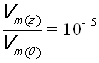 , тогда:
, тогда:

4. Определим отношение модуля плотности тока проводимости к модулю плотности тока смещения.
По условию задачи ![]() , соответветственно здесь плоская электромагнитная волна распространяется как в реальной среде, а в реальных средах, в отличии от свободного пространства потери волны возникают по двум причинам. Во-первых, потери связаны с конечной проводимостью среды (потери на джоулевое тепло), во вторых, потери возникают из-за явления поляризации диэлектрика, которое в конечном счете также приводит к тепловым потерям. Характер потерь можно оценить вычислив отношение модуля плотностей тока проводимости и тока смещения:
, соответветственно здесь плоская электромагнитная волна распространяется как в реальной среде, а в реальных средах, в отличии от свободного пространства потери волны возникают по двум причинам. Во-первых, потери связаны с конечной проводимостью среды (потери на джоулевое тепло), во вторых, потери возникают из-за явления поляризации диэлектрика, которое в конечном счете также приводит к тепловым потерям. Характер потерь можно оценить вычислив отношение модуля плотностей тока проводимости и тока смещения:
 ; (1.78 [1])
; (1.78 [1])
Это отношение называется тангенсом угла потерь. В нашем случае, согласно вычислений по (2.12 [2]), ![]() .
.
Задача 2
Цилиндрический резонатор имеет диаметр D = 0,06 м, длину 0,05 м, заполнен полиэтиленом (относительная проницаемость ![]() = 2,5). Определить: 1.Резонансную частоту колебания E
= 2,5). Определить: 1.Резонансную частоту колебания E![]() .
.
2.Резонансную частоту колебания H![]() .
.
3.Добротность колебания E![]() при значении поверхностного сопротивления R
при значении поверхностного сопротивления R![]() Ом/м.
Ом/м.
4.Полосу пропускания резонатора на колебании E![]() .
.
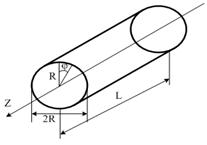
Рис.10 Цилиндрический резонатор
Дано: D=0,06м; ![]() =2,5; l=0,05м;
=2,5; l=0,05м;
Решение.
1.Определим резонансную частоту колебания E010.
Резонансная частота ![]() определяется по формуле:
определяется по формуле:
 ; (11.18[5]), где
; (11.18[5]), где
![]() - фазовая скорость волны, равная:
- фазовая скорость волны, равная:
![]() (3.39[5]), где
(3.39[5]), где
![]() - скорость света, (3.38)[5].
- скорость света, (3.38)[5].
![]() относительная магнитная проницаемость среды =1
относительная магнитная проницаемость среды =1
Подставляя значения в (3.39[5]) получаем:
![]() ;
;
![]() корень функции Бесселя для волны Е010
корень функции Бесселя для волны Е010![]() (табл.9.4 [5]);
(табл.9.4 [5]);
a – радиус резонатора, a =![]() ;
;
р – индекс, для волны Е010 р=0, тогда ![]() будет равна:
будет равна:
![]()
2.Определим резонансную частоту колебания H111.
Резонансная частота ![]() определяется по формуле:
определяется по формуле:
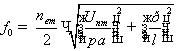 , (11.18[5]), где
, (11.18[5]), где
![]() - корень функции Бесселя для волны Н111
- корень функции Бесселя для волны Н111![]() (табл.9.4 [5]);
(табл.9.4 [5]);
для волны H111 р=1, тогда ![]() будет равна:
будет равна:
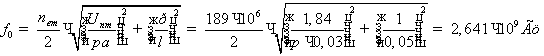
3.Определим добротность колебания E010 при значении поверхностного сопротивления RS= 10–3 Сим/м.
Формула добротности для волны Е010 имеет вид:
![]() , (11.32 [1]);
, (11.32 [1]);
Подставляя значения в (11.32 [1]), получаем:
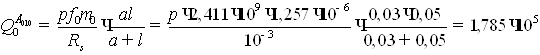
4. Определим полосу пропускания резонатора на колебании E010.
Полоса пропускания П равна:
 ; (стр.259 [5])
; (стр.259 [5])

Литература
1. Пименов Ю.В., Вольман В.И., Муравцов А.Д. /Техническая электродинамика /Под ред. Ю.В. Пименова: Учеб. пособие для вузов.— М.: Радио и связь, 2000.— 536с.: ил.
2. Баскаков С.И. Электродинамика и распространение радиоволн: Учеб.пособие для вузов по спец. «Радиотехника». —М.Высш.шк.,1992. —416с.: ил.
3. Федоров Н.Н. Основы электродинамики: Учеб. пособие для вузов.—М.: «Высш. школа», 1980.—399с., ил.
4. Андрусевич Л.К., Беленький В.Г. Основы электродинамики. Учебное пособие., «СибГУТИ», 2005. 163с.
5. Семенов Н.А. Техническая электродинамика. Учебное пособие для вузов. М., «Связь», 1973. 480с.
Похожие работы
... и магнитные потоки. «... в бегущей плоской электромагнитной волне электрическая энергия в любой момент равна магнитной.» Общий курс физики. Электричество. Д.В.Сивухин. 1996. Т.3. Ч.2. С.18. Например, в дискретной электромагнитной волне - фотоне энергия электрического потока равна энергии магнитного потока: Wэ = Wм = eФ0v, т.е. электромагнитная энергия фотона: W = Wэ + Wм = 2eФ0v. Если E = ...
... переменного тока проводимости или тока смещения, где длина волны зависит от частоты колебания. Любой электрический ток, согласно электродинамике, всегда замкнут. Поэтому продольные электромагнитные волны всегда замкнуты независимо от того, представляют они переменный электрический ток проводимости или смещения. Продольные электрические возмущения поля имеют продольную ориентацию электрического ...
... переходит в энергию вылетевших электронов. Остальная часть поглощенных световых квантов ведет к нагреванию металлов. Шкала электромагнитных волн Электромагнитные излучения с различными длинами волн имеют довольно много различий, но все они, от радиоволн и да гамма-излучения, одной физической природы. Все виды электромагнитного излучения в большей или меньшей степени проявляют свойства ...
... , хотя изучение поведения бегущих волн в замкнутых системах представляет и чисто практический интерес. В настоящей работе проведено экспериментальное исследование поведения бегущих электромагнитных волн в волноводном тракте. Целью настоящей работы являлось исследование частотной зависимости амплитуды бегущей электромагнитной волны в кольцевом волноводном тракте. Для этого необходимо было решить ...

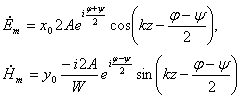
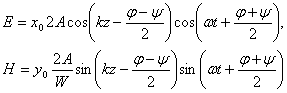
0 комментариев