Навигация
Метод узловых напряжений (потенциалов)
3. Метод узловых напряжений (потенциалов)
Сущность метода заключается в том, что в качестве неизвестных принимаются узловые напряжения (потенциалы) независимых узлов цепи относительно одного узла, выбранного в качестве опорного или базисного. Потенциал базисного узла принимается равным нулю, и расчет сводится к определению (q-1) узловых напряжений, существующих между остальными узлами и базисным.
Уравнения узловых напряжений в канонической форме при числе независимых узлов n=q-1 имеют вид
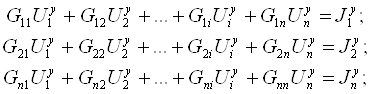
Коэффициент ![]() называется собственной проводимостью n-го узла. Собственная проводимость равна сумме проводимостей всех ветвей, присоединенных к узлу n.
называется собственной проводимостью n-го узла. Собственная проводимость равна сумме проводимостей всех ветвей, присоединенных к узлу n.
Коэффициент ![]() называется взаимной или межузловой проводимостью. Она равна взятой со знаком «минус» сумме проводимостей всех ветвей, соединяющих напрямую узлы i и n.
называется взаимной или межузловой проводимостью. Она равна взятой со знаком «минус» сумме проводимостей всех ветвей, соединяющих напрямую узлы i и n.
Правая часть уравнений (9) называется узловым током, Узловой ток равен алгебраической сумме всех источников тока, подключенных к рассматриваемому узлу, плюс алгебраическая сумма произведений ЭДС источников на проводимость ветви с ЭДС
![]()
При этом со знаком «плюс» слагаемые записываются в том случае, если ток источника тока и ЭДС источника напряжения направлены к узлу, для которого составляется уравнение.
Приведенная закономерность определения коэффициентов существенно упрощает составление уравнений, которое сводится к записи симметричной матрицы узловых параметров
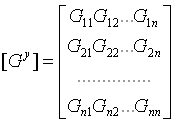
и вектора узловых токов источников
![]()
Уравнения узловых напряжений можно записать в матричной форме
![]() .
.
Если в какой-либо ветви заданной схемы содержатся только идеальный источник ЭДС (сопротивление этой ветви равно нулю, т.е. проводимость ветви равна бесконечности), целесообразно в качестве базисного выбрать один из двух узлов, между которыми включена эта ветвь. Тогда потенциал второго узла становится также известным и равным по величине ЭДС (с учетом знака). В этом случае для узла с известным узловым напряжением (потенциалом) уравнение составлять не следует и общее число уравнений системы уменьшается на единицу.
Решая систему уравнений (9), определяем узловые напряжения, а затем по закону Ома определяем токи в ветвях. Так для ветви, включенной между узлами m и n ток равен

При этом с положительным знаком записываются те величины (напряжения, ЭДС), направление которых совпадает с выбранным координатным направлением. В нашем случае (11) – от узла m к узлу n. Напряжение между узлами ![]() определяется через узловые напряжения
определяется через узловые напряжения
![]() .
.
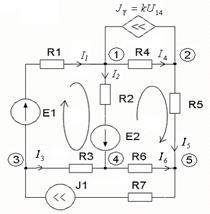
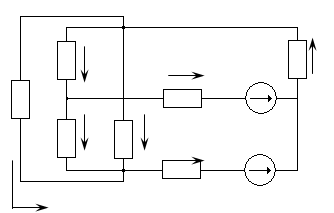
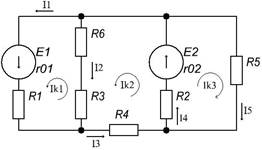
Рассмотрим метод узловых напряжений на примере электрической цепи, схема которой представлена на рис. 4.
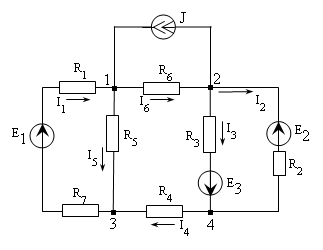
Рис. 4
Определяем число узлов (в данном примере число узлов q=4) и обозначаем их на схеме.
Так как схема не содержит идеальных источников напряжения, то в качестве базисного может быть выбран любой узел, например узел 4.
При этом ![]() .
.
Для остальных независимых узлов схемы (q-1=3) составляем уравнения узловых напряжений в канонической форме.
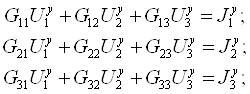
Определяем коэффициенты уравнений.
Собственные проводимости узлов

Взаимные (межузловые) проводимости
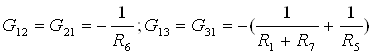
![]()
Определяем узловые токи.
Для 1-го узла
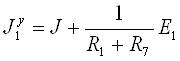 .
.
Для 2-го узла
 .
.
Для 3-го узла
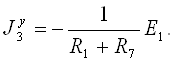
Подставив значения коэффициентов (проводимостей) и узловых токов в уравнения (12), определяем узловые напряжения ![]()
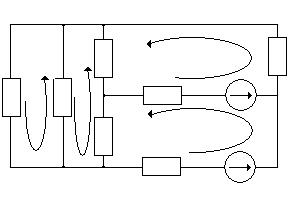
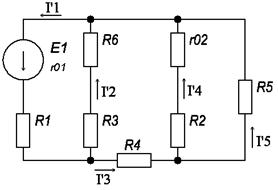
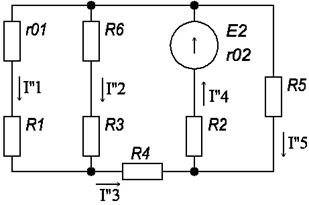
Прежде чем перейти к определению токов ветвей, задаемся их положительным направлением и наносим на схему (рис. 5).
Токи определяем по закону Ома. Так, например, ток ![]() направлен от узла 3 к узлу 1. Так же направлена и ЭДС
направлен от узла 3 к узлу 1. Так же направлена и ЭДС ![]() этой ветви. Следовательно
этой ветви. Следовательно
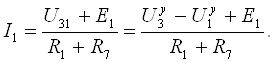
Токи остальных ветвей определяем по тому же принципу
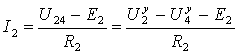
Так как ![]() то
то
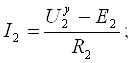
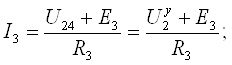
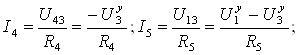
Похожие работы
... тока, а реакция – это токи ветвей и напряжения между какими - то точками схемы. Поэтому любой ток или напряжение в линейной цепи с несколькими источниками равен сумме частичных значений тока или напряжения, вызванных действием каждого источника в отдельности. Свойство наложения (суперпозиции) справедливо только для токов и напряжений. Для мощностей этот принцип не выполняется, так как мощности ...
... неровностей на поверхности анода, т.е. происходит его полировка. 2 Расчётная часть 2.1Задание на курсовую работу Расчет разветвлённой электрической цепи постоянного тока. Для заданной электрической цепи необходимо: 1) Записать систему уравнений по законам Кирхгофа (без расчетов); 2) Определить все токи и ...
... будущего специалиста к работе на производстве. 1. Анализ электрического состояния линейных электрических цепей постоянного тока Схема электрической цепи постоянного тока: R2 I2 R7 I5 E1,r02 I7 R1 I3 R5 R3 R4 I4 I6 I1 E2,r02 R6 Рис.1.0 ...
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...




0 комментариев