Навигация
Анализ матрицы коэффициентов парных корреляций для абсолютных величин
4. Анализ матрицы коэффициентов парных корреляций для абсолютных величин
Таблица 5
| № фактора | Y | X1 | X2 | X3 | X4 | X5 | X6 |
| Y | 1.00 | 0.52 | -0.22 | -0.06 | -0.23 | 0.44 | 0.12 |
| X1 | 0.52 | 1.00 | 0.38 | 0.52 | 0.38 | 0.74 | 0.60 |
| X2 | -0.22 | 0.38 | 1.00 | 0.91 | 1.00 | 0.68 | 0.74 |
| X3 | -0.06 | 0.52 | 0.91 | 1.00 | 0.91 | 0.86 | 0.91 |
| X4 | -0.23 | 0.38 | 1.00 | 0.91 | 1.00 | 0.67 | 0.74 |
| X5 | 0.44 | 0.74 | 0.68 | 0.86 | 0.67 | 1.00 | 0.85 |
| X6 | 0.12 | 0.60 | 0.74 | 0.91 | 0.74 | 0.85 | 1.00 |
Из таблицы 4 находим тесно коррелирующие факторы. Налицо мультиколлениарность факторов Х2 и Х4 . Оставим только один фактор Х2 . Так же достаточно высокий коэффициент корреляции ( 0.91 ) между факторами Х2 и Х3 . Избавимся от фактора Х3 .
5. Построение уравнения регрессии для абсолютных величин
Проведём многошаговый регрессионный анализ для оставшихся факторов : Х1 , Х2 , Х5 , Х6 .
а) Шаг первый .
Y = 12. 583 + 0 * X1 + 0.043 * X2 + 0.021 * X5 - 0.368 * X6
Коэффициент множественной корреляции = 0.861
Коэффициент множественной детерминации = 0.742
Сумма квадратов остатков = 32.961
t1 = 0.534 *
t2 = 2.487
t5 = 2.458
t6 = 0.960 *
У фактора Х1 t-критерий оказался самым низким . Следовательно фактором Х1 можно пренебречь . Вычеркнем этот фактор .
б) Шаг второй.
Y = 12.677 - 0.012 * X2 + 0.023 * X5 - 0.368 * X6
Коэффициент множественной корреляции = 0.854
Коэффициент множественной детерминации = 0.730
Сумма квадратов остатков = 34.481
t2 = 2.853
t5 = 3.598
t6 = 1.016 *
У фактора Х6 t-критерий оказался самым низким . Следовательно фактором Х6 можно пренебречь . Вычеркнем этот фактор .
в) Шаг третий .
Y = 12.562 - 0.005 * X2 + 0.018 * X5
Коэффициент множественной корреляции = 0.831
Коэффициент множественной детерминации = 0.688
Сумма квадратов остатков = 39.557
t2 = 3.599
t5 = 4.068
В результате трёхшаговой регрессии мы получили рабочее уравнение.
6. Анализ матрицы коэффициентов парных корреляций для относительных величин
Таблица 5
| № фактора | Y | X1 | X2 | X3 | X4 | X5 | X6 |
| Y | 1.00 | 0.14 | -0.91 | 0.02 | -0.88 | -0.01 | -0.11 |
| X1 | 0.14 | 1.00 | -0.12 | -0.44 | -0.17 | -0.09 | 0.02 |
| X2 | -0.91 | -0.12 | 1.00 | -0.12 | 0.98 | -0.01 | -0.38 |
| X3 | 0.02 | -0.44 | -0.12 | 1.00 | 0.00 | 0.57 | 0.34 |
| X4 | -0.88 | -0.17 | 0.98 | 0.00 | 1.00 | 0.05 | -0.05 |
| X5 | -0.01 | -0.09 | -0.01 | 0.57 | 0.05 | 1.00 | 0.25 |
| X6 | -0.11 | 0.02 | -0.38 | 0.34 | -0.05 | 0.25 | 1.00 |
В таблице выявляем тесно коррелирующие факторы. Таким образом, не трудно заметить достаточно высокий коэффициент корреляции между факторами Х2 и Х4. Избавимся от Х2
7. Построение уравнения регрессии для относительных величин
а) Шаг первый .
Y = 25,018+0*Х1+
Коэффициент множественной корреляции = 0,894
Коэффициент множественной детерминации = 0.799
Сумма квадратов остатков = 26,420
t1 = 0,012*
t2 = 0,203*
t3 =0.024*
t4 =4.033
t5 = 0.357*
t6 = 0.739 *
У фактора Х1 t-критерий оказался самым низким . Следовательно фактором Х1 можно пренебречь . Вычеркнем этот фактор .
б) Шаг второй .
Y = e ^3.141 * X2^(-0.722) * X5^0.795 * X6^(-0.098)
Коэффициент множественной корреляции = 0.890
Коэффициент множественной детерминации = 0.792
Сумма квадратов остатков = 0.145
t2 = 4.027
t5 = 4.930
t6 = 0.623 *
У фактора Х6 t-критерий оказался самым низким . Следовательно фактором Х6 можно принебречь . Вычеркнем этот фактор .
в) Шаг третий .
Y = e ^3.515 * X2^(-0.768) * X5^0.754
Коэффициент множественной корреляции = 0.884
Коэффициент множественной детерминации = 0.781
Сумма квадратов остатков = 0.153
t2 = 4.027
t5 = 4.930
В результате трёхшаговой регрессии мы получили рабочее уравнение :
Y =
Экономический смысл модели :
При увеличении расходов на подготовку и освоение производства производительность труда будет увеличиваться . Это означает что на данных предприятиях есть резервы для расширения производства , для введения новых технологий и инноваций с целью увеличения прибыли .
При увеличении заработной платы производительность труда будет снижаться . Это , скорее всего , будет происходить из-за того , что рабочие на данных предприятиях получают и так высокие зарплаты , либо фонд заработной платы используется по максимуму и дальнейший его рост приведёт к непредвиденным расходам .
8. Сравнительный анализ линейной и степенной моделей
Сравнивая линейную и степенную регрессионную модель видим , что статистические характеристики степенной модели превосходят аналогичные характеристики линейной модели . А именно : коэффициент множественной детерминации у степенной модели равен 0.781 , а у линейной - 0.688 . Это означает , что факторы , вошедшие в степенную модель , объясняют изменение производительности труда на 78.1 % , тогда как факторы , вошедшие в линейную модель , - на 68,8 % ; сумма квадратов остатков степенной модели ( 0.153 ) значительно меньше суммы квадратов остатков линейной модели ( 39.557 ) . Следовательно значения полученные с помощью степенной модели близки к фактическим .
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.cooldoclad.narod.ru/
Похожие работы
... ресурсу про x1=10, х2=25. 7. Функции спроса и предложения на товар имеют вид: d(p) = - 0,3p + 60 и S(p) = 9,7p+10, соответственно. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ Билет № 2 1. В чем состоит связь целевых функций прямой и двойственной задач и что это значит ...
... и 25 ед. полезности. Товары приобретаются по ценам 50 у.е. и 70 у.е., бюджет потребителя составляет 2000 у.е. Сформулировать задачу потребителя. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ Билет № 11 Рассматривается задача составления плана производства как Задача линейного ...
... ед. и 25 ед. полезности. Товары приобретаются по ценам 50 у.е. и 70 у.е., бюджет потребителя составляет 2000 у.е. Сформулировать задачу потребителя. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ Билет № 11 1) Рассматривается задача составления плана производства как Задача ...
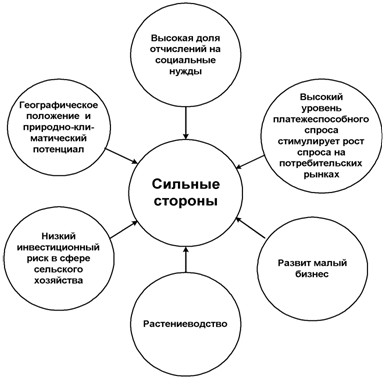
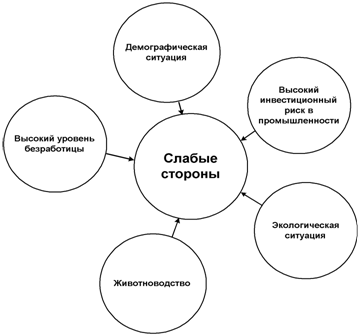
... . Слабые стороны социально-экономического положения в Орловской области (рис. 2.2). Рисунок 2.2 – Результат SWOT-анализа: слабые стороны социально-экономического положения Орловской области В соответствии со статистическими данными в Орловской области наблюдается снижение развития животноводства. До конца 2008 года сохранялась тенденция сокращения крупного рогатого скота в ...
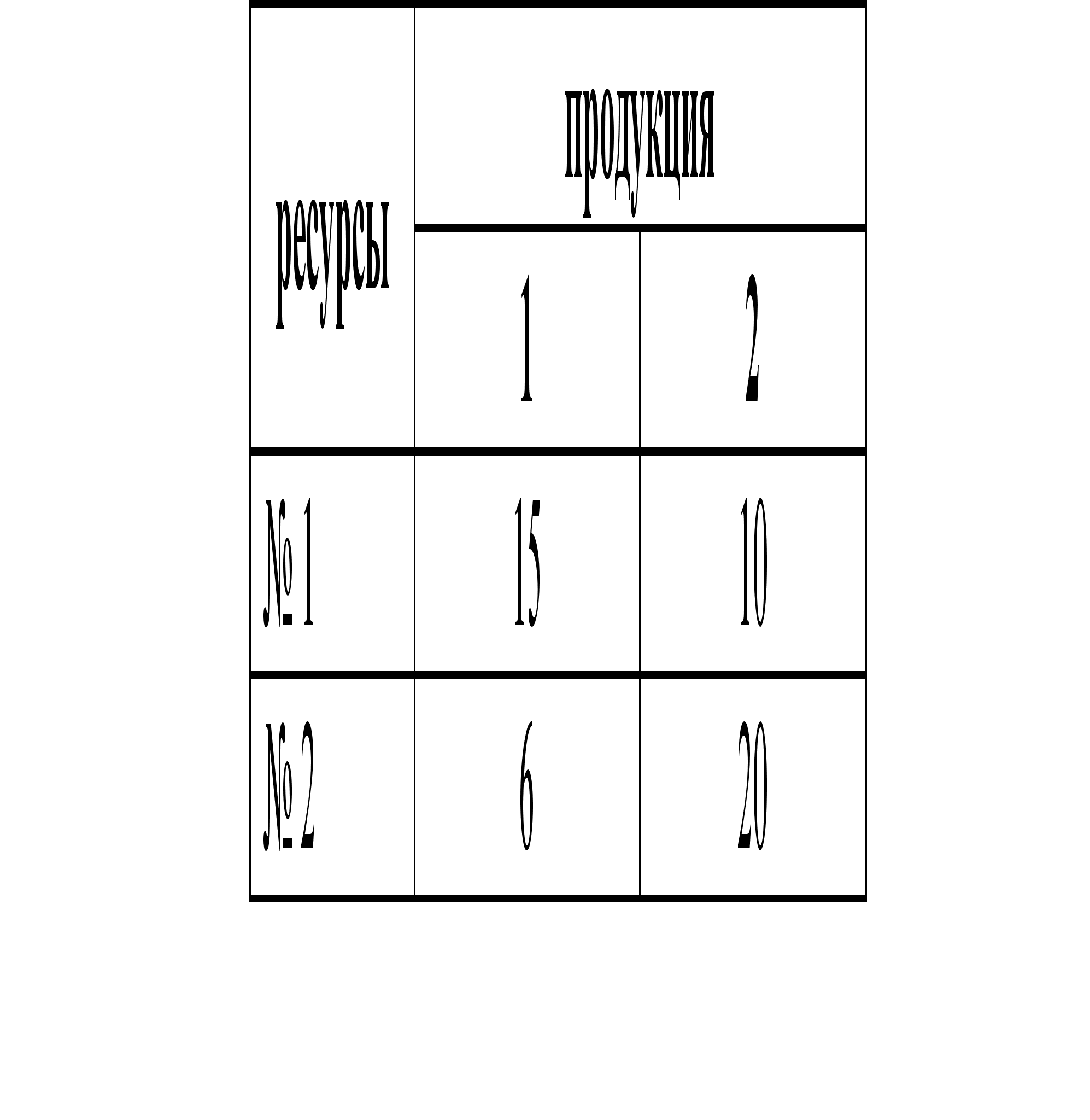
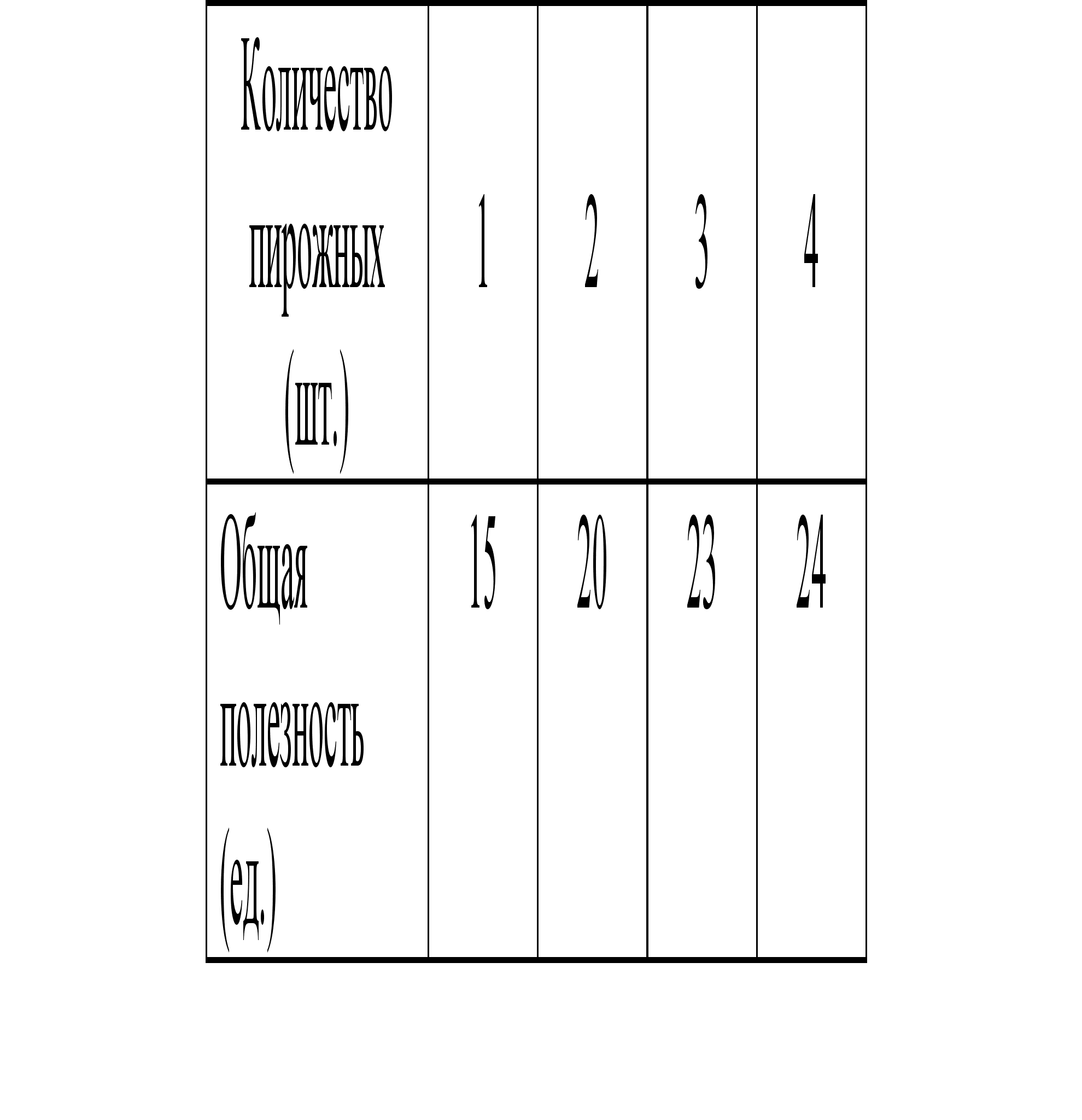
0 комментариев