Парадокс Санчо Пансы

3. Парадокс Санчо Пансы

Один старый, известный еще в Древней Греции парадокс обыгрывается в «Дон Кихоте» М. Сервантеса. Санчо Панса сделался губернатором острова Баратария и вершит суд. Первым к нему является какой-то приезжий и говорит: – Сеньор, некое поместье делится на две половины многоводной рекой… Так вот, через эту реку переброшен мост, и тут же с краю стоит виселица и находится нечто вроде суда, в коем обыкновенно заседает четверо судей, и судят они на основании закона, изданного владельцем реки, моста и всего поместья, каковой закон составлен таким образом: «Всякий проходящий по мосту через сию реку долженствует объявить под присягою: куда и зачем он идет, и кто скажет правду, тех пропускать, а кто солжет, тех без всякого снисхождения отправлять на находящуюся тут же виселицу и казнить». С того времени, когда этот закон во всей своей строгости был обнародован, многие успели пройти через мост, и как скоро судьи удовлетворялись, что прохожие говорят правду, то пропускали их. Но вот однажды некий человек, приведенный к присяге, поклялся и сказал: он-де клянется, что пришел за тем, чтобы его вздернули вот на эту самую виселицу, и ни за чем другим. Клятва сия привела судей в недоумение, и они сказали: «Если позволить этому человеку беспрепятственно следовать дальше, то это будет означать, что он нарушил клятву и согласно закону повинен смерти; если же мы его повесим, то ведь он клялся, что пришел только за тем, чтобы его вздернули на эту виселицу, следовательно, клятва его, выходит, не ложна, и на основании того же самого закона надлежит пропустить его». И вот я вас спрашиваю, сеньор губернатор, что делать судьям с этим человеком, ибо они до сих пор недоумевают и колеблются…

Санчо предложил, пожалуй, не без хитрости: ту половину человека, которая сказала правду, пусть пропустят, а ту, которая соврала, пусть повесят, и таким образом правила перехода через мост будут соблюдены по всей форме. Этот отрывок интересен в нескольких отношениях.

Прежде всего, он является наглядной иллюстрацией того, что с описанным в парадоксе безвыходным положением вполне может столкнуться – и не в чистой теории, а на практике – если не реальный человек, то хотя бы литературный герой. Выход, предложенный Санчо Панса, не был, конечно, решением парадокса. Но это было как раз, то решение, к которому только и оставалось прибегнуть в его положении.

Когда-то Александр Македонский вместо того, чтобы развязывать хитрый гордиев узел, чего еще никому не удалось сделать, просто разрубил его. Подобным же образом поступил и Санчо. Пытаться решить головоломку на ее собственных условиях, было бесполезно – она попросту неразрешима. Оставалось отбросить эти условия и ввести свое.

И еще один момент. Сервантес этим эпизодом явно осуждает непомерно формальный, пронизанный духом схоластической логики масштаб средневековой справедливости. Но какими распространенными в его время – а это было около четырехсот лет назад – были сведения из области логики! Не только самому Сервантесу известен данный парадокс. Писатель находит возможным приписать своему герою, безграмотному крестьянину, способность понять, что перед ним неразрешимая задача!

4. Парадокс брадобрея

Самым знаменитым из открытых уже в нашем веке парадоксов является антиномия, обнаруженная Б. Расселом. Идея носилась в воздухе, и ее опубликование произвело впечатление разорвавшейся бомбы. Этот парадокс вызвал в математике, по мнению Д. Гильберта, «эффект полной катастрофы». Нависла угроза над самыми простыми и важными логическими методами, самыми обыкновенными и полезными понятиями. Сразу же стало очевидным, что ни в логике, ни в математике за всю долгую историю их существования не было выработано решительно ничего, что могло бы послужить основой для устранения антиномии. Явно оказался необходимым отход от привычных способов мышления.

Парадокс Рассела в первоначальной его форме связан с понятием множества, или класса. Можно говорить о множествах различных объектов, например о множестве всех людей или о множестве натуральных чисел. Элементом первого множества будет всякий отдельный человек, элементом второго – каждое натуральное число. Допустимо также сами множества рассматривать как некоторые объекты и говорить о множествах множеств. Можно ввести даже такие понятия, как множество всех множеств или множество всех понятий. Относительно любого произвольно взятого множества представляется осмысленным спросить, является оно своим собственным элементом или нет. Множества, не содержащие себя в качестве элемента, назовем обычными. Например, множество всех людей не является человеком, так же как множество атомов – это не атом. Необычными будут множества, являющиеся собственными элементами. Например, множество, объединяющее все множества, представляет собой множество и, значит, содержит само себя в качестве элемента. Очевидно, что каждое множество является либо обычным, либо необычным.

Рассмотрим теперь множество всех обычных множеств. Поскольку оно множество, о нем тоже можно спрашивать, обычное оно или необычное. Ответ, однако, оказывается обескураживающим. Если оно обычное, то согласно своему определению должно содержать само себя в качестве элемента, поскольку содержит все обычные множества. Но это означает, что оно является необычным множеством. Допущение, что наше множество представляет собой обычное множество, приводит, таким образом, к противоречию. Значит, оно не может быть обычным. С другой стороны, оно не может быть также необычным: необычное множество содержит само себя в Качестве элемента, а элементами нашего множества являются только обычные множества. В итоге приходим к заключению, что множество всех обычных множеств не может быть ни обычным, ни необычным множеством.

Итак, множество всех множеств, не являющихся собственными элементами, есть свой элемент в том и только том случае, когда оно не является таким элементом. Это явное противоречие.

Противоречие говорит о том, что такого множества просто не существует. Но почему оно не может существовать? Ведь оно состоит из объектов, удовлетворяющих четко определенному условию, причем само условие не кажется каким-то исключительным или неясным. Если столь просто и ясно заданное множество не может существовать, то в чем, собственно, заключается различие между возможными и невозможными множествами? Вывод о несуществовании рассматриваемого множества звучит неожиданно и внушает беспокойство. Он делает наше общее понятие множества аморфным и хаотичным, и нет гарантии, что оно не способно породить какие-то новые парадоксы.

Парадокс Рассела замечателен своей крайней общностью. Для его построения не нужны какие-либо сложные технические понятия, как в случае некоторых других парадоксов, достаточно понятий «множества» и «элемента множества». Но эта простота как раз и говорит о его фундаментальности: он затрагивает самые глубокие основания наших рассуждений о множествах, поскольку говорит не о каких-то специальных случаях, а о множествах вообще.

Парадокс Рассела не имеет специфически математического характера. В нем используется понятие множества, но не затрагиваются какие-то особые, связанные именно с математикой его свойства. Это становится очевидным, если переформулировать парадокс в чисто логических терминах.

О каждом свойстве можно, по всей вероятности, спрашивать, приложимо оно к самому себе или нет. Свойство быть горячим, например, неприложимо к самому себе, поскольку само не является горячим; свойство быть конкретным тоже не относится к самому себе, ибо это абстрактное свойство. Но вот свойство быть абстрактным, являясь абстрактным, приложимо к самому себе. Назовем эти неприменимые к самим себе свойства неприложимыми. Применимо ли свойство быть неприложимым к самому себе? Оказывается, что неприложимость является неприложимой только в том случае, если она не является таковой. Это, конечно, парадоксально, Логическая, касающаяся свойств разновидность антиномии Рассела столь же парадоксальна, как и математическая, относящаяся к множествам, ее разновидность.

Б. Рассел предложил также следующий популярный вариант открытого им парадокса. «Брадобрей бреет всех тех и только тех жителей города, которые не бреются сами. Кто бреет брадобрея?» Парадокс брадобрея заключается в том, что, якобы, нельзя ответить на этот вопрос.

Чтобы понять ситуацию, разобьем жителей города на три группы. Это разбиение показано на левом рисунке: те, кто бреется самостоятельно, – сверху; те, кого бреют, – снизу; кто вообще не бреется (монахи, дети, женщины…) – вне эллипса.

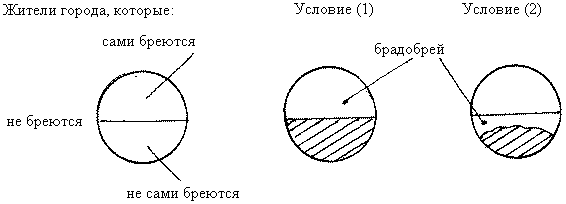
Рассмотрим сначала действие условия (1). Пусть брадобрей бреет всех тех, которые не сами бреются, то есть всю нижнюю половину эллипса (штриховка отмечает клиентов брадобрея). Но условие (1) разрешает ему брить и того, кто сам бреется, то есть самого себя. Условие (1) разрешает ему расположиться в верхней половине эллипса, где жители сами бреются, и брить себя там. Это показано на среднем рисунке.

Если же действует условие (2), и брадобрей бреет только тех, которые не сами бреются, это означает, что он бреет часть нижней половины эллипса и не бреет себя, то есть не находится в верхней половине эллипса. Но жители из нижней половины могут быть побриты не брадобреем, а кем-то еще. И брадобрей может находиться среди этих людей (правый рисунок). Так что брадобрея может брить его приятель, а брадобрей будет брить заштрихованную часть нижней половины эллипса.

Но если действуют оба условия, (1) и (2), то брадобрею нет места в эллипсе. Он, значит, не бреется вообще. И тут нет никакого парадокса. Он, сталь быть, либо монах, либо робот, либо ребенок, либо женщина, либо не житель города… А если в городе нет никого, кроме бреющихся мужчин, и, стало быть, внешность эллипса пуста, то брадобрей, удовлетворяющий условиям (1) и (2), попросту не существует. Нелепо спрашивать в этом случае, кто его бреет. Множество таких брадобреев – пусто.

И тут мы заметим, что заданный вопрос, «Кто бреет брадобрея?», был некорректен с самого начала так же, как классический вопрос: «Зачем ты бьешь своего отца?» Прежде, чем спрашивать, кто бреет брадобрея, надо получить согласие, что его кто-то бреет.

Рассуждение о парикмахере может быть названо псевдопарадоксом. По своему ходу оно строго аналогично парадоксу Рассела и этим интересно. Но оно все-таки не является подлинным парадоксом.

Другой пример такого же псевдопарадокса представляет собой известное рассуждение о каталоге.

Некая библиотека решила составить библиографический каталог, в который входили бы все те и только те библиографические каталоги, которые не содержат ссылки на самих себя. Должен ли такой каталог включать ссылку на себя? Нетрудно показать, что идея создания такого каталога неосуществима; он просто не может существовать, поскольку должен одновременно и включать ссылку на себя и не включать. Интересно отметить, что составление каталога всех каталогов, не содержащих ссылки на самих себя, можно представить как бесконечный, никогда не завершающийся процесс.

Допустим, что в какой-то момент был составлен каталог, скажем К1 включающий все отличные от него каталоги, не содержащие ссылки на себя. С созданием K1 появился еще один каталог, не содержащий ссылки на себя. Так как задача заключается в том, чтобы составить полный каталог всех каталогов, не упоминающих себя, то очевидно, что K1 не является ее решением. Он не упоминает один из таких каталогов – самого себя. Включив в K1 это упоминание о нем самом, получим каталог К2. В нем упоминается К1 но не сам К2. Добавив к К2 такое упоминание, получим К3, который опять-таки неполон из-за того, что не упоминает самого себя. И так далее без конца.