Навигация
Замена платежей и их консолидация
1. Замена платежей и их консолидация
На практике нередко возникают случаи, когда необходимо заменить одно обязательство другим, например с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи) и т.п. В таких ситуациях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменения контракта.
Для сопоставления альтернативных вариантов ставки, используемые в условиях контрактов, приводят к единому показателю.
Различные финансовые схемы можно считать эквивалентными в том случае, если они приводят к одному и тому же финансовому результату.
Эквивалентная процентная ставка – это ставка, которая для рассматриваемой финансовой операции даст точно такой же денежный результат (наращенную сумму), что и применяемая в этой операции ставка.
Классическим примером эквивалентности являются номинальная и эффективная ставка процентов:
i = (1 + j/m)m - 1
j = m[(1 + i)1/m - 1]
Эффективная ставка измеряет тот относительный доход, который может быть получен в целом за год, т.е. совершенно безразлично – применять ли ставку j при начислении процентов m раз в год или годовую ставку i, – и та, и другая ставки эквивалентны в финансовом отношении.
Поэтому совершенно не имеет значения, какую из приведенных ставок указывать в финансовых условиях, поскольку использование их дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку, а в европейских странах предпочитают эффективную ставку процентов.
Если две номинальные ставки определяют одну и ту же эффективную ставку процентов, то они называются эквивалентными.
Пример. Каковы будут эквивалентные номинальные процентные ставки с полугодовым начислением процентов и ежемесячным начислением процентов, если соответствующая им эффективная ставка должна быть равна 25%?
Решение:Находим номинальную ставку для полугодового начисления процентов:
j = m[(1 + i)1/m - 1] = 2[(1 + 0,25)1/2 - 1] = 0,23607
Находим номинальную ставку для ежемесячного начисления процентов:
j = m[(1 + i)1/m - 1] = 4[(1 + 0,25)1/12 - 1] = 0,22523
Таким образом, номинальные ставки 23,61% с полугодовым начислением процентов и 22, 52% с ежемесячным начислением процентов являются эквивалентными.
При выводе равенств, связывающих эквивалентные ставки, приравниваются друг к другу множители наращения, что дает возможность использовать формулы эквивалентности простых и сложных ставок:
простая процентная ставка
i = [(1 + j/m)mn - 1]/n
сложная процентная ставка
![]()
Пример. Предполагается поместить капитал на 4 года либо под сложную процентную ставку 20% годовых с полугодовым начислением процентов, либо под простую процентную ставку 26% годовых. Найти оптимальный вариант.
Решение:Находим для сложной процентной ставки эквивалентную простую ставку:
i = [(1 + j/m)mn - 1]/n = [(1 + 0,2/2)2 • 4 - 1]/4 = 0,2859
Таким образом, эквивалентная сложной ставке по первому варианту простая процентная ставка составляет 28,59% годовых, что выше предлагаемой простой ставки в 26% годовых по второму варианту, следовательно, выгоднее разместить капитал по первому варианту, т.е. под 20% годовых с полугодовым начислением процентов.
Находим эквивалентную сложную ставку процентов для простой ставки:
![]()
Таким образом, процентная ставка 18,64% годовых с полугодовым начислением процентов ниже 20% годовых с полугодовым начислением процентов, то первый вариант выгоднее.
В практической деятельности часто возникает необходимость изменения условий ранее заключенного контракта – объединение нескольких платежей или замене единовременного платежа рядом последовательных платежей. Естественно, что в таких условиях ни один из участников финансовой операции не должен терпеть убыток, вызванный изменением финансовых условий. Решение подобных задач сводится к построению уравнения эквивалентности, в котором сумма заменяемых платежей, приведенная к какому-то одному моменту времени, приравнена к сумме платежей по новому обязательству, приведенному к тому же моменту времени.
Для краткосрочных контрактов консолидация осуществляется на основе простых ставок. В случае с объединением (консолидированием) нескольких платежей в один сумма заменяемых платежей, приведенных к одной и той же дате, приравнивается к новому обязательству:
FVo = ΣFVj • (1 + i •╥tj),
где tj – временной интервал между сроками, tj = n0 - nj.
Пример. Решено консолидировать два платежа со сроками 20.04 и 10.05 и суммами платежа 20 тыс. руб. и 30 тыс. руб. Срок консолидации платежей 31.05. Определить сумму консолидированного платежа при условии, что ставка равна 10% годовых.
Решение:Определим временной интервал между сроками для первого платежа и консолидированного платежа (дата выдачи и дата погашения считается за один день):
t1= 11(апрель) + 31(май) - 1= 41 день;
для второго платежа и консолидированного платежа:
t2 = 22(май) - 1 = 21 день.
Отсюда сумма консолидированного платежа будет равна:
FVoб. = FV1 • (1 + t1/T • i) + FV2 • (1 + t2/T • i) =
= 20'000 • (1 + 41/360 • 0,1) + 30'000 • (1 + 21/360 • 0,1) = 50'402,78 руб.
Таким образом, консолидированный платеж со сроком 31.05 составит 50'402,78 руб.
Конечно, существуют различные возможности изменения условий финансового соглашения, и в соответствии с этим многообразие уравнений эквивалентности. Готовыми формулами невозможно охватить все случаи, возникающие в практической деятельности, но в каждой конкретной ситуации при замене платежей уравнение эквивалентности составляется похожим образом.
Если платеж FV1 со сроком n1 надо заменить платежом FVоб. со сроком nоб (nоб > n1) при использовании сложной процентной ставки i, то уравнение эквивалентности имеет вид:
FVоб. = FV1 • (1 + i)nоб.-n1
Пример. Предлагается платеж в 45 тыс. руб. со сроком уплаты через 3 года заменить платежом со сроком уплаты через 5 лет. Найти новую сумму платежа, исходя из процентной ставки 12 % годовых.
Решение:Поскольку nоб. > n1, то платеж составит:
FVоб. = FV1 (1 + i)nоб.-n1 = 45'000 (1 + 0,12)5-3 = 56'448 руб.
Таким образом, в новых условиях финансовой операции будет предусмотрен платеж 56'448 руб.
Таким образом, операции по консолидированию долга - преобразование краткосрочной задолженности с фиксированной ставкой процента в долгосрочную задолженность с фиксированной ставкой процента (консолидированный долг), консолидированная задолженность погашается примерно равными годовыми долями в течение п лет.
Похожие работы
... И. только коммерческих документов. ИНКОТЕРМС (англ. Incoterms) - изданный Международной торговой палатой сборник международных торговых терминов, обобщающий опыт мировой коммерческой практики; в настоящее время действует в редакции 1990 г. ИНТЕГРАЦИЯ ЭКОНОМИЧЕСКАЯ (англ. economic integration) - формирование (при активном участии государственных структур) устойчивых всесторонних связей между ...
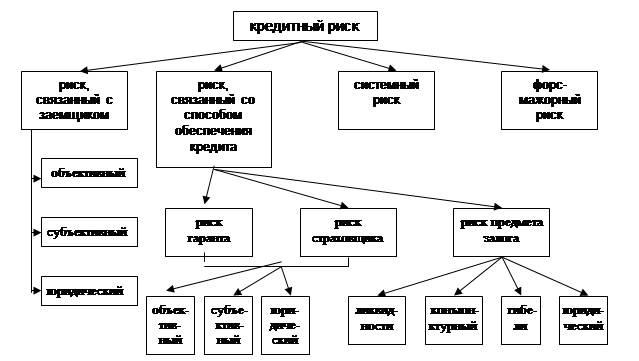
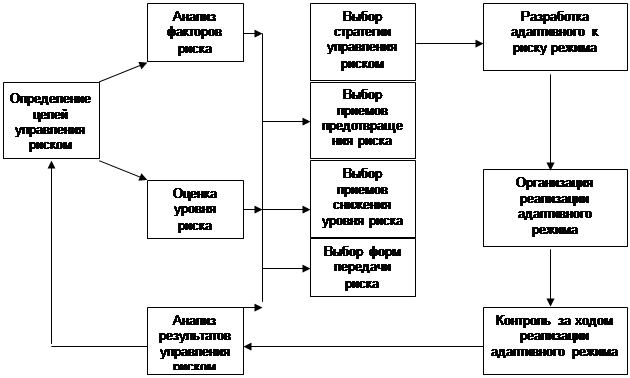
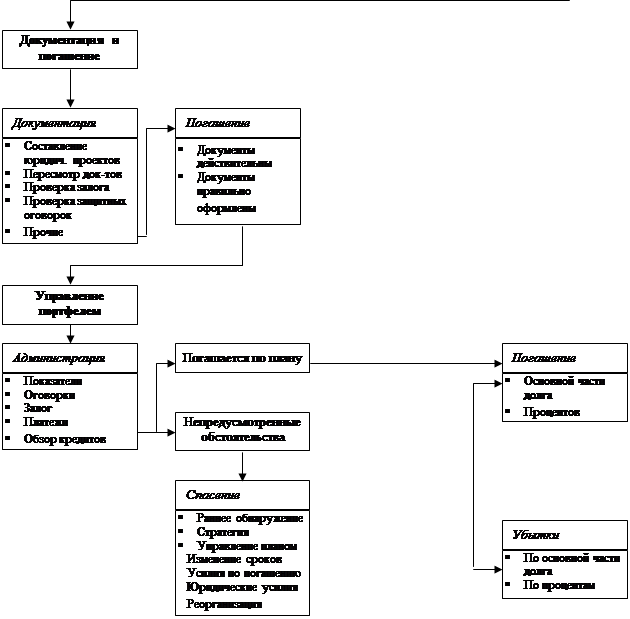
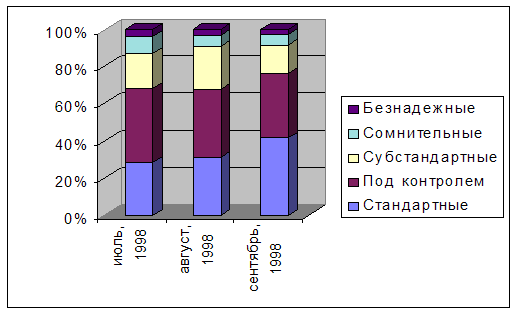
... настоящей дипломной работе на примере работы одного из ведущих коммерческих банков Украины (далее Банк) будет представлена система управления кредитным риском и наиболее эффективные способы его минимизации. 1.4. Сущность и содержание риск-менеджмента Управление и риск – взаимосвязанные компоненты. Если говорить о теории управления риском, то здесь необходимо отметить, что, как и любая ...
... в виде декларации. За правильностью уплаты налогов следит налоговая инспекция, главная обязанность которой — сбор налогов и других обязательных платежей в бюджет. 2 ПУТИ РЕФОРМИРОВАНИЯ НАЛОГОВОЙ СИСТЕМЫ РФ 2.1 Направления налоговой реформы Основы налоговой системы будут определяться новым Налоговым Кодексом РФ. Надо сказать, что ряд принципиальных положений проекта Налогового Кодекса ...
... в соответствии с социально-экономической сущностью государства, в зависимости от взглядов правящей политической партии, требований момента и потребности правительства в доходах. Современные налоговые системы используют оба принципа налогообложения, в зависимости от экономической и социальной целесообразности. Элементы налога и виды ставок Налоговая система базируется на соответствующих ...

0 комментариев