Навигация
Виды, сингонии, категории
1.2 Виды, сингонии, категории
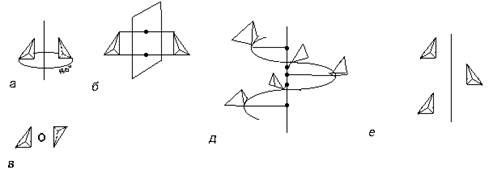
Каждый многогранник обладает определенной симметрией. Совокупность элементов симметрии, свойственная многограннику, называется видом симметрии. Всего выведено 32 вида симметрии. Логичный вывод всех видов симметрии был сделан русским ученым А.В.Гадолиным в 1869 году.
Виды симметрии сгруппированы в сингонии - группы с общими чертами структуры.
В триклинную сингонию объединены два вида симметрии с осями первого порядка -L1 и Li1, то есть - С.
В моноклинную сингонию объединяются виды симметрии с одной осью симметрии второго порядка - простой или инверсионной.
В ромбическую сингонию объединяются виды симметрии с несколькими осями второго порядка - простыми или инверсионными.
Внешняя симметрия кристаллов триклинной, моноклинной, ромбической сингоний, объединяемых в низшую категорию, связана с их структурой.
В тригональную сингонию объединяются виды симметрии, имеющие одну ось третьего порядка, в тетрагональную - одну ось четвертого порядка, в гексагональную - одну ось шестого порядка. Эти три сингонии, характеризующиеся наличием одной оси высшего порядка, объединяются в среднюю категорию.
В высшую категорию включается кубическая сингония, характеризующаяся наличием нескольких осей 3-го и 4-го порядка. Осей шестого порядка в кубической сингонии нет.
1.3 Простые формы кристаллов
Названия геометрических фигур в кристаллографии несколько отличаются от фигур в геометрии. Это связано с тем, что в кристаллографии учитывается структура вещества кристалла.
Простой формой кристалла называется совокупность граней, связанных элементами симметрии. Различается несколько типов простых форм (табл.1):
· Открытые формы - такие формы, грани которых не полностью ограничивают пространство. Примерами таких форм являются: моноэдр, диэдр, пинакоид, призмы и пирамиды.
· Замкнутые формы - такие формы, грани которых полностью ограничивают пространство. Примерами таких форм являются:
. дипирамиды, трапецоэдры, скаленоэдры, тетраэдры, все простые
формы кубической сингонии.
· Конгруэнтные формы - это совместимые формы. Примеры: гексаэдр, октаэдр, призмы, пирамиды.
· Энантиоморфные формы - зеркально совместимые формы правые и левые. Примеры: ромбический тетраэдр, трапецоэдры, пентагонтриоктаэдр, тетрагонтриоктаэдр.
· Постоянными формами - называются такие формы, грани котороых образуют постоянные углы и постоянные символы. Пример: гексаэдр, октаэдр, кубический тетраэдр.
· Переменными формами - называются формы, грани которых образуют переменные углы и переменные символы. Примерами могут быть пирамиды, дипирамиды, ромбоэдр, тетраэдр.
1.3.1 Простые формы низшей категории
Таблица 1
Определение простых форм низшей категории| № п/п | Кол-во граней | Взаимное расположение граней | Названия простых форм |
| 1 2 3 4 5 6 7 | 1 2 2 4 4 4 8 | - Параллельны Пересекаются Пересекаются в параллельных ребрах, в сечении ромб Пересекаются в одной точке, в сечении ромб Пересекаются в 4-х точках по три, грань- косоугольный треугольник Пересекаются в 2-х точках с общим ромбическим сечением | моноэдр пинакоид диэдр призма ромбическая пирамида ромбическая тетраэдр ромбический дипирамида ромбическая |
В низшей категории насчитывается 7 простых форм - из них 5 открытых и 2 замкнутые - тетраэдр и дипирамида ромбическая (табл.1, рис.1).
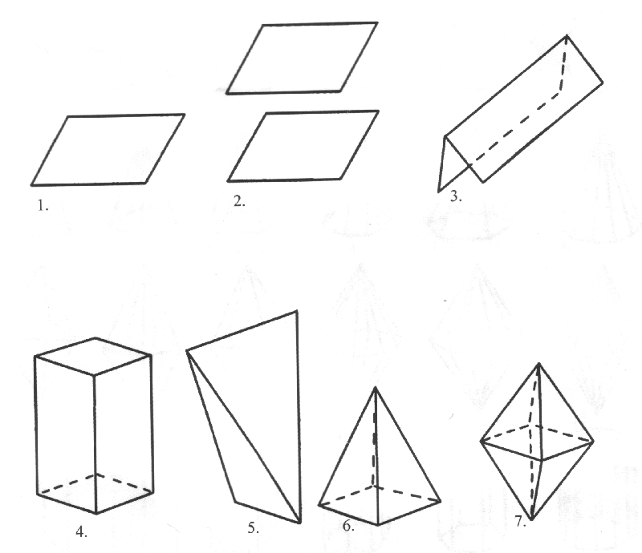
Рис.1 Простые формы кристаллов низшей категории:
1 - моноэдр; 2 - пинакоид; 3 - диэдр; 4 - ромбическая призма;
5 - ромбический тетраэдр; 6 - ромбическая пирамида; 7 - ромбическая
дипирамида
1.3.2 Простые формы средней категорииИз низшей категории в среднюю категорию переходят две простые формы: моноэдр и пинакоид. Они переходят как частные формы, т.е. перпендикулярные главной оси. Другие формы - 6 призм, 6 пирамид, 6 дипирамид, 3 трапецоэдра, 2 скаленоэдра, тетраэдр, ромбоэдр. Своих форм в средней категории - 25, и две переходящие из низшей категории (табл. 2, рис.2).
К открытым формам относятся призмы и пирамиды. чтобы образовать из них замкнутые многогранники, требуется моноэдр или пинакоид.
Остальные формы - трапецоэдры, скаленоэдры, тетраэдр и ромбоэдр - являются замкнутыми и переменными.
Таблица 2
Определение простых форм средней категории
| Пересечение с главной осью | Расположение граней относительно главной оси | Названия простых форм | Кол-во граней | |
| не пересекают главную ось | Параллельные главной оси |
тетрагональная гексагональная дитригональная дитетрагональная дигексагональная | 3 4 6 6 8 12 | |
| пересекают главную ось | Пересекают главную ось
Пересекают главную ось в одной точке | моноэдр пинакоид
тетрагональная гексагональная дитригональная дитетрагональная дигексагональная | 1 2 3 4 6 6 8 12 | |
| пересекают главную ось в 2-х точках | А. Нижние грани точно под верхними
Б. Нижние грани несимметричны верхним
В. Нижняя грань симметрична двум верхним
Г. Нижняя пара граней симметрична двум парам верхних |
тетрагональная гексагональная дитригональная дитетрагональная дигексагональная
тетрагональный гексагональный тетраэдр ромбоэдр
дитригональный | 6 8 12 12 16 24 6 8 12 4 6 8 12 | |
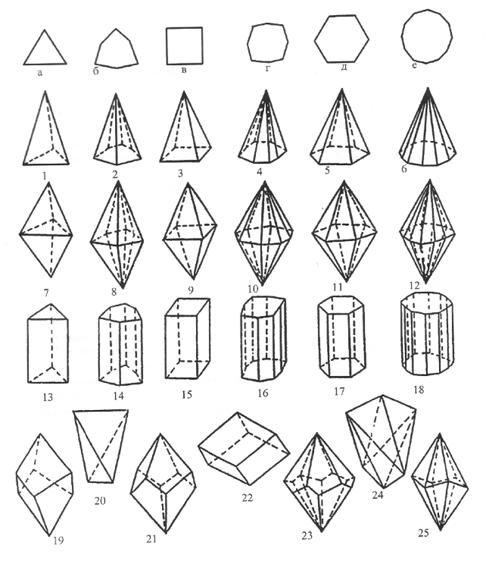
Рис. 2. Простые формы кристаллов средней категории:
1–6 пирамиды: 1–тригональная, 2–дитригональная, 3–тетрагональная,
4–дитетрагональная, 5–гексагональная, 6–дигексагональная;
7–12 дипирамиды: 7–тригональная, 8–дитригональная, 9–тетрагональная, 10–дитетрагональная, 11–гексагональная, 12–дигексагональная;
13–25 призмы; 13–тригональная, 14–дитригональная, 15–тетрагональная, 16–дитетрагональная, 17–гексагональная, 18–дигексагональная, 19–тригональный трапецоэдр, 20–тетраэдр, 21–тетрагональный трапецоэдр, 22–ромбоэдр, 23–гексагональный трапецоэдр, 24–тетрагональный скаленоэдр, 25–тригональный скаленоэдр
1.3.3 Простые формы высшей категории
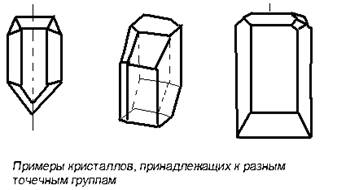
В высшей категории - кубической сингонии насчитывается 15 простых форм (табл.3, рис. 3). Ни одна простая форма из низшей и средней категорий не переходит в высшую. Некоторое исключение составляет тетраэдр. В низшей категории его грани косоугольные треугольники, в средней категории - равнобедренные треугольники, в высшей категории - равносторонние треугольники.
Таблица 3 Определение простых форм высшей категории| № п/п | Названия простых форм | Кол-во граней | Форма граней | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 2 3. 4 5 6 7 8 9 10 11 12 13 14 15 | Тетраэдр Тригонтритетраэдр Тетрагонтритетраэдр Пентагонтритетраэдр Тригонгексатетраэдр Гексаэдр Тригонтетрагексаэдр Октаэдр Тригонтриоктаэдр Тетрагонтриоктаэдр Пентагонтриоктаэдр Тригонгексаоктаэдр Ромбододекаэдр Пентагондодекаэдр Дидодекаэдр | 4 12 12 12 24 6 24 8 24 24 24 48 12 12 24 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание. Все формы замкнутые. Постоянные формы подчеркнуты, остальные переменные.
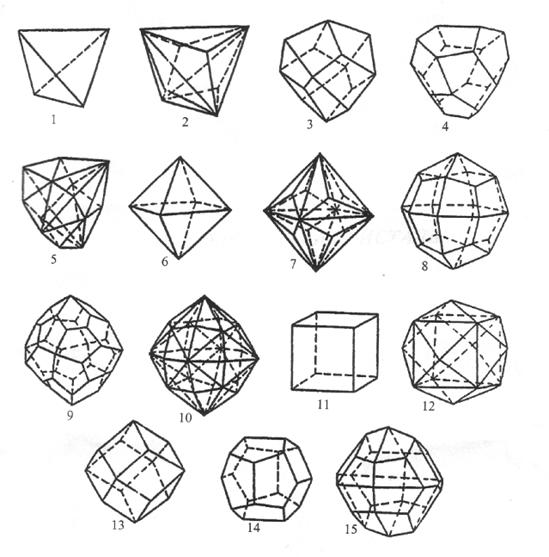
Рис.3 Простые формы кристаллов высшей категории:
1–тетраэдр; 2–тригонтритетраэдр; 3–тетрагонтритетраэдр; 4–пентагонтритетраэдр; 5–гексатетраэдр; 6–октаэдр; 7–тригонтриоктаэдр; 8–тетрагонтриоктаэдр; 9–пентагонтриоктаэдр; 10–гексагонтриоктаэдр; 11–гексаэдр; 12–тригонтетрагексаэдр; 13–ромбододекаэдр; 14–пентагондодека- эдр; 15–дидодекаэдр
Комбинационной формой - называется такая, которая состоит из 2-х и более простых форм. Действительно, одной плоскостью не ограничить многогранник, двумя и тремя также. Лишь четырьмя плоскостями можно ограничить пространство и получить четырехгранник - тетраэдр. Открытые формы - призмы и пирамиды - также нуждаются в дополнительных плоскостях, чтобы получился многогранник. В замкнутых формах нет такой необходимости.
Похожие работы
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
... , в результате чего сформировались натечные образования оникса, малахита, кальцита и др. В зависимости от применения коллекционный материал подразделяется на несколько видов: для учебных коллекций, научных исследований, минералогических музеев, личных сборов. Месторождения драгоценных камней часто являются вторичными. Благодаря процессам выветривания первичных месторождений драгоценные камни, ...
... двум. Верхняя граница, напротив, размыта и неотчетлива. Но ясно, что она должна находиться в той области, где добавление еще одного члена уже не изменяет свойств кластера: в этой области и заканчивается переход из количества в качество. Ниже мы увидим, что эта граница не вполне однозначна, но практически большая часть изменений, существенных для химика, заканчивается при ~103 частицах в группе. ...
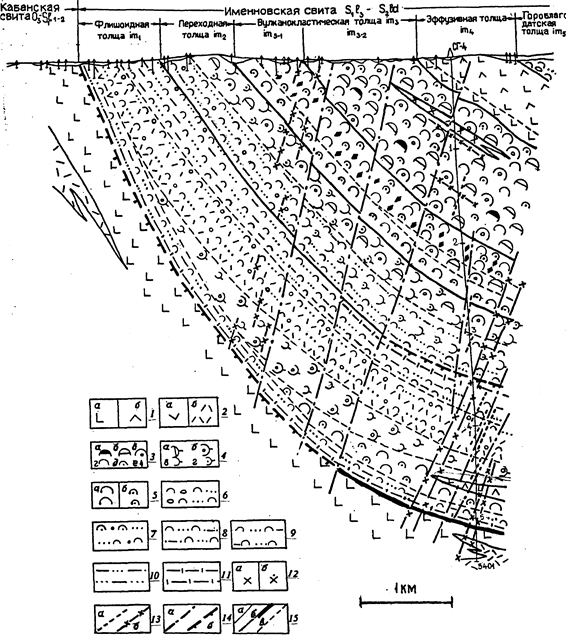
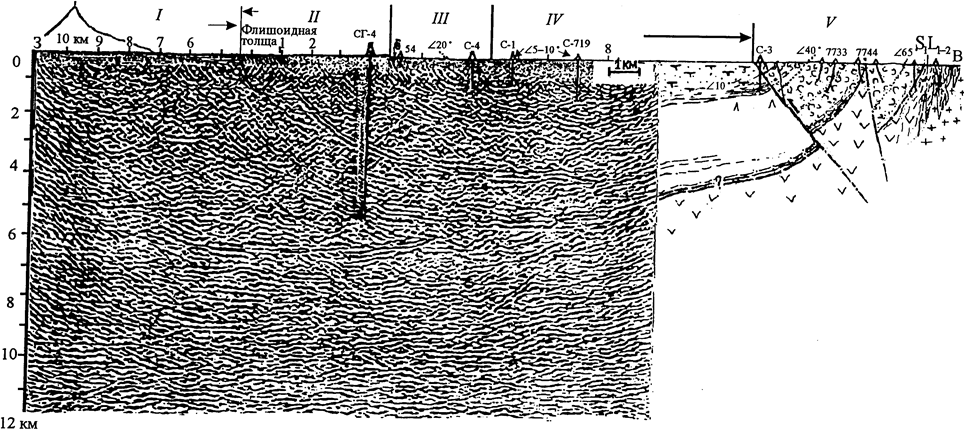
... без сопровождения структурного бурения достаточной координации. Необходимо ускорить обоснование и реализацию геолого-геофизического (геодинамического) полигона вокруг СГ-4. В направлении повышения научной эффективности сверхглубокого бурения необходимо существенно усилий исследовательские возможности на самой скважине, особенно систематических замеров на больших глубинах флюидного трещинно- ...




0 комментариев