Навигация
Портфель Марковица максимальной эффективности
3.3.2 Портфель Марковица максимальной эффективности
![]() Модель оптимального портфеля Марковица, которая обеспечивает максимальную доходность при заданном риске(
Модель оптимального портфеля Марковица, которая обеспечивает максимальную доходность при заданном риске(![]() =0.88) имеет вид:
=0.88) имеет вид:
![]()
![]()
|
| (3.5) |
![]()
Решая задачу с помощью табличного процессора Excel и его надстройки Поиск решения, получим (рис. 3.2):
![]() =7,9%
=7,9%
х1 =0,56; х2=0; х3=0; х4=0,05; х5=0,39.
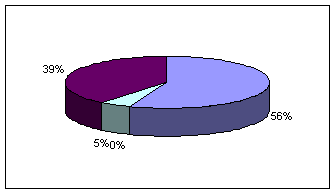
Рис. 3.2 – Оптимальный портфель ценных бумаг Марковица максимальной эффективности
3.4 Оптимальный портфель ценных бумаг Тобина3.4.1 Портфель Тобина минимального риска
Через несколько лет после исследования Марковица другой крупнейший американский экономист Д. Тобин заметил, что если на рынке есть безрисковые бумаги (к таким можно отнести с некоторой натяжкой государственные ценные бумаги), то решение задачи об оптимальном портфеле сильно упрощается и приобретает новое качество.
Пусть ![]() - эффективность безрисковых бумаг (12%), а х0 – доля капитала, вложенного в них, тогда в рисковую часть портфеля вложена
- эффективность безрисковых бумаг (12%), а х0 – доля капитала, вложенного в них, тогда в рисковую часть портфеля вложена ![]() часть всего капитала. Пусть
часть всего капитала. Пусть ![]() - эффективность и
- эффективность и ![]() – вариация (дисперсия) рисковой части портфеля и
– вариация (дисперсия) рисковой части портфеля и ![]() – риск этой рисковой части. Тогда эффективность всего портфеля равна
– риск этой рисковой части. Тогда эффективность всего портфеля равна ![]() , вариация портфеля равна
, вариация портфеля равна ![]() и риск портфеля равен
и риск портфеля равен ![]() (считается, что безрисковые бумаги некоррелированны с остальными). Исключая
(считается, что безрисковые бумаги некоррелированны с остальными). Исключая ![]() , получим
, получим ![]() , т.е. эффективность портфеля линейно зависит от его риска. Задача Марковица об оптимальном портфеле в этом случае такова:
, т.е. эффективность портфеля линейно зависит от его риска. Задача Марковица об оптимальном портфеле в этом случае такова:
|
| (3.6) |
Изложим теперь окончательное решение этой задачи, полученное Тобиным. Пусть V – матрица ковариаций рисковых ценных бумаг, ![]() - вектор-столбцы долей х капитала, вкладываемых в i – ый вид рисковых ценных бумаг и ожидаемых эффективностей этого вида,
- вектор-столбцы долей х капитала, вкладываемых в i – ый вид рисковых ценных бумаг и ожидаемых эффективностей этого вида, ![]() . Пусть также I n – мерный вектор-столбец, компоненты которого равны 1. тогда оптимальное значение долей
. Пусть также I n – мерный вектор-столбец, компоненты которого равны 1. тогда оптимальное значение долей ![]() есть
есть
|
| (3.7) |
Здесь ![]() - матрица, обратная к V. В числителе дроби стоит число, в знаменателе, если выполнить все действия (операция транспонирования первого сомножителя в знаменателе не указана, но подразумевается), тоже получится число, причем константа, определяемая рынком и не зависящая от инвестора,
- матрица, обратная к V. В числителе дроби стоит число, в знаменателе, если выполнить все действия (операция транспонирования первого сомножителя в знаменателе не указана, но подразумевается), тоже получится число, причем константа, определяемая рынком и не зависящая от инвестора, ![]() - вектор-столбец размерности n. Как видим, этот вектор не зависит от эффективности портфеля
- вектор-столбец размерности n. Как видим, этот вектор не зависит от эффективности портфеля ![]() . Таким образом, вектор долей рисковых видов ценных бумаг, пропорциональный этому вектору также не зависит от
. Таким образом, вектор долей рисковых видов ценных бумаг, пропорциональный этому вектору также не зависит от ![]() . Следовательно, структура рисковой части портфеля не зависит от
. Следовательно, структура рисковой части портфеля не зависит от ![]() . Однако сумма компонент вектора
. Однако сумма компонент вектора ![]() зависит от
зависит от ![]() , а именно, компоненты вектора
, а именно, компоненты вектора ![]() пропорционально увеличиваются с ростом
пропорционально увеличиваются с ростом ![]() , поэтому доля
, поэтому доля ![]() безрисковые вложений будет при этом сокращаться. Выразим риск оптимального портфеля в зависимости от его доходности. Для этого в формулу вариации портфеля
безрисковые вложений будет при этом сокращаться. Выразим риск оптимального портфеля в зависимости от его доходности. Для этого в формулу вариации портфеля ![]() подставим оптимальный вектор
подставим оптимальный вектор ![]() из формулы (15.3) через
из формулы (15.3) через ![]() . Получим
. Получим
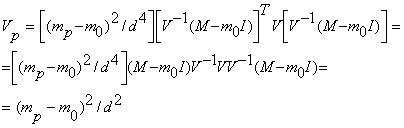
Окончательно:
![]() или
или
|
| (3.8) |
Можно также написать выражение эффективности оптимального портфеля от его риска: ![]() или
или ![]() . Видно, что эти зависимости линейные.
. Видно, что эти зависимости линейные.
Полученный оптимальный портфель называется портфелем Тобина минимального риска, т.е. портфель Тобина – это портфель Марковица при наличии на рынке безрисковых бумаг.
Решая задачу с помощью табличного процессора Excel и его надстройки Поиск решения, получим:
![]() =0,51
=0,51
х0=0,08; х1 =0,25; х2=0; х3=0; х4=0,44; х5=0,23.
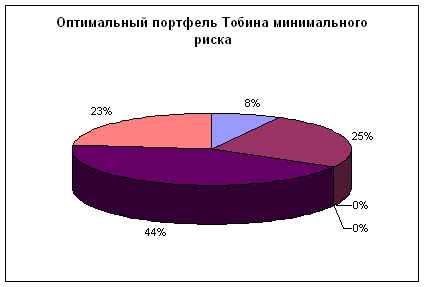
Рис. 3.3 – Оптимальный портфель ценных бумаг Тобина минимального риска.
Похожие работы
... валютных операций банка В результате проведенного анализа предлагается комплекс мероприятий по увеличению доходности банка от проведения валютных операций. На современном этапе развития увеличение прибыли возможно за счет совершенствования уже внедренных операций и введения новых. На основании проведенного в данной дипломной работе анализа валютных операций предлагаются следующие пути по ...
... информационных технологий в банковском бизнесе, что значительно повышает уровень обслуживания клиентов. 3. РАЗРАБОТКА ПРАКТИЧЕСКИХ РЕКОМЕНДАЦИЙ ПО РАБОТЕ С VIP-КЛИЕНТАМИ 3.1. Организация работы с VIP-клиентом 3.1.1. Поиск крупных клиентов Будет большой ошибкой для банка, если клиентская база в глазах его руководителей будет представлена неким однородным монолитом, с которым ведется ...
... основе кредитной истории "прошлых" клиентов банк пытается определить, какая вероятность того, что конкретный потенциальный заемщик вернет кредит в определенный срок. Скоринг используется главным образом во время кредитования физических лиц, особенно при выдаче потребительских кредитов, не обеспеченных залогом. Основное задание скоринга заключается в том, чтобы выяснить не только, состоятельный ...
... теоретические основы кредитования, сущность, назначение и роль кредита, его формы, виды и функции, а также вопрос влияния на экономику ссудного процента. Во втором разделе будет проведен анализ порядка установления, начисления и взыскания процентов по кредитам на примере кредитного продукта «овердрафт» на основе данных по КБ «Приватбанк». 2. Анализ порядка установления, начисления и взыскания ...
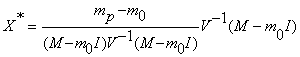

0 комментариев