Навигация
Рассчитать матрицу парных коэффициентов корреляции; оценить статистическую значимость коэффициентов регрессии
1. Рассчитать матрицу парных коэффициентов корреляции; оценить статистическую значимость коэффициентов регрессии.
2. Оценить статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения проверить с помощью F-критерия; оценить качество уравнения регрессии с помощью коэффициента детерминации.
Таблица 2.
| Переменная | Описание |
| № | номер торговой точки |
| price | цена колготок в рублях |
| DEN | плотность в DEN |
| polyamid | содержание полиамида в % |
| lykra | содержание лайкры в % |
| firm | фирма-производитель: 0 - Sanpellegrino, 1 - Грация |
3. Построить уравнение множественной регрессии только со статистически значимыми факторами.
4. Отобразить графически исходные данные и расчетные значения.
РЕШЕНИЕ ЗАДАЧИ
1. Рассчитать матрицу парных коэффициентов корреляции; оценить статистическую значимость коэффициентов регрессии.
Сначала нужно отобрать факторы, которые должны войти в модель. Для этого строится матрица коэффициентов парной корреляции (табл.3.)
Таблица 3.
|
| Y | X1 | X2 | X3 | X4 |
| Y | 1 | ||||
| X1 | 0,071711 | 1 | |||
| X2 | -0,55678 | -0,42189 | 1 | ||
| X3 | 0,607569 | 0,435579 | -0,66726 | 1 | |
| X4 | -0,12119 | -0,10354 | 0,060901 | -0,43912 | 1 |
Анализ показал, что независимые переменные Х2 (полиамид) и Х3 (лайкра) имеют тесную линейную связь с результативным фактором Y. Проверяем наличие мультипликативности: │ ![]() │= 0,66726. Считается, что две переменных явно коллинеарны, т.е. находятся между собой в линейной зависимости, если
│= 0,66726. Считается, что две переменных явно коллинеарны, т.е. находятся между собой в линейной зависимости, если ![]() ≥ 0,7. Х2 и Х3 могут включаться в модель, т.к. мультипликативности нет. Х1 и Х4 в незначительной степени влияют на Y, их отбрасываем.
≥ 0,7. Х2 и Х3 могут включаться в модель, т.к. мультипликативности нет. Х1 и Х4 в незначительной степени влияют на Y, их отбрасываем.
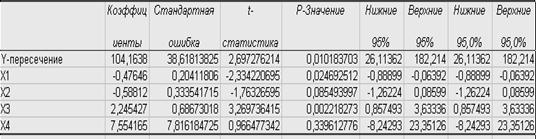
Коэффициенты множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов. Для упрощения работы эти коэффициенты можно получить в Excel с помощью отчета по регрессии. Получаем уравнение линейной модели: у = -0,476х1-0,588х2+2,245х3+7,554х4+ 104,163.
Это означает, что с увеличением лайкры в составе колготок на 1%, их цена поднимется на 2,245 у.е. А при увеличении полиамида в составе колготок на 1%, их цена упадет на 0,588 у.е.
2. Оценить статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения проверить с помощью F-критерия; оценить качество уравнения регрессии с помощью коэффициента детерминации.
Подставляя значения факторов Х в уравнение регрессии, вычисляем урасч,а записываем ряд остатков, составляем таблицу 4.
Таблица 4.
| № | prise | polyamid | lykra | у расч. | остатки |
|
| Y | X2 | X3 |
|
|
| 1 | 49,36 | 86 | 14 | 75,4920707 | -26,1321 |
| 2 | 22,51 | 97 | 3 | 51,8771925 | -29,3672 |
| 3 | 22,62 | 97 | 3 | 51,8771925 | -29,2572 |
| 4 | 59,89 | 90 | 17 | 79,8758598 | -19,9859 |
| 5 | 71,94 | 79 | 21 | 90,5623507 | -18,6224 |
| 6 | 71,94 | 79 | 21 | 90,5623507 | -18,6224 |
| 7 | 89,9 | 85 | 15 | 81,1152196 | 8,78478 |
| 8 | 74,31 | 85 | 13 | 71,8598003 | 2,4502 |
| 9 | 77,69 | 88 | 10 | 63,359152 | 14,33085 |
| 10 | 60,26 | 86 | 14 | 73,5171042 | -13,2571 |
| 11 | 111,19 | 82 | 18 | 77,2971365 | 33,89286 |
| 12 | 73,56 | 83 | 14 | 75,2814724 | -1,72147 |
| 13 | 84,61 | 84 | 16 | 71,6300376 | 12,97996 |
| 14 | 49,9 | 82 | 18 | 84,8513019 | -34,9513 |
| 15 | 89,9 | 85 | 15 | 68,7964882 | 21,10351 |
| 16 | 96,87 | 85 | 15 | 64,0319222 | 32,83808 |
| 17 | 39,99 | 98 | 2 | 29,9853791 | 10,00462 |
| 18 | 49,99 | 76 | 24 | 84,769301 | -34,7793 |
| 19 | 49,99 | 83 | 17 | 67,7240545 | -17,7341 |
| 20 | 49,99 | 88 | 10 | 49,065454 | 0,924546 |
| 21 | 49,99 | 76 | 24 | 80,004735 | -30,0147 |
| 22 | 49,99 | 42 | 8 | 66,8636812 | -16,8737 |
| 23 | 129,9 | 50 | 42 | 130,949041 | -1,04904 |
| 24 | 84 | 82 | 18 | 77,2971365 | 6,702864 |
| 25 | 61 | 86 | 14 | 75,4920707 | -14,4921 |
| 26 | 164,9 | 16 | 30 | 155,377089 | 9,522911 |
| 27 | 49,9 | 82 | 18 | 84,8513019 | -34,9513 |
| 28 | 89,9 | 85 | 15 | 81,1152196 | 8,78478 |
| 29 | 129,9 | 50 | 42 | 130,949041 | -1,04904 |
| 30 | 89,9 | 86 | 14 | 73,5171042 | 16,3829 |
| 31 | 105,5 | 85 | 15 | 76,3506536 | 29,14935 |
| 32 | 79,9 | 88 | 12 | 79,7614203 | 0,13858 |
| 33 | 99,9 | 88 | 12 | 77,3791373 | 22,52086 |
| 34 | 99,9 | 73 | 25 | 110,626959 | -10,727 |
| 35 | 119,9 | 85 | 12 | 79,1435056 | 40,75649 |
| 36 | 109,9 | 83 | 14 | 84,8106044 | 25,0894 |
| 37 | 59,9 | 86 | 14 | 75,4920707 | -15,5921 |
| 38 | 79,9 | 82 | 18 | 77,2971365 | 2,602864 |
| 39 | 82,9 | 86 | 14 | 75,4920707 | 7,407929 |
| 40 | 111,8 | 82 | 18 | 77,2971365 | 34,50286 |
| 41 | 83,6 | 82 | 18 | 77,2971365 | 6,302864 |
| 42 | 60 | 86 | 14 | 75,4920707 | -15,4921 |
| 43 | 80 | 82 | 18 | 77,2971365 | 2,702864 |
| 44 | 90 | 76 | 24 | 89,533867 | 0,466133 |
| 45 | 120 | 74 | 26 | 85,6718339 | 34,32817 |
Расчет остатков связан с тем, что изменение уi будет неточно описываться изменением Х, поскольку присутствуют другие факторы, неучтенные в данной модели.
В Excel находим t-критерий для х2 и х3. ![]() =-1,763;
=-1,763; ![]() =3,270. Сравним с табличным
=3,270. Сравним с табличным ![]() (0,05;42)=2,023.
(0,05;42)=2,023.
При │tрасч│>tα связь существует и коэффициент корреляции является статистически значимым. В данном случае значимым является только а3. На практике на а2 (коэффициент содержания полиамида в составе колготок при определении цены) опираться не стоит, т.к. этот коэффициент не является статистически значимым.
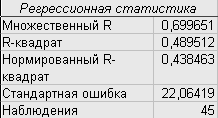
Приступая к оценке значимости уравнения множественной регрессии через критерий Фишера, найдем Fрасч (есть в отчете по регрессии)=9,589 и Fтабл(0,05;2;42)=3,220. Т.к. Fрасч> Fтабл, то модель является в целом надежной и по ней можно строить прогноз.
Оценить коэффициенты регрессии можно также с помощью коэффициента детерминации R2. В данном случае он равен 0,4895 (из отчета по регрессии). Это говорит о том, что 48,95% всех случайных изменений у зависят от х и объясняются регрессионной моделью и учтены в ряде остатков. Для практического применения модели это очень маленький процент, и от нее следует отказаться. Для множественной регрессии применяют также скорректированный коэффициент детерминации ![]() 1-(1-R2)
1-(1-R2)![]() = 0,4385. Модель имеет низкую точность.
= 0,4385. Модель имеет низкую точность.
3. Построить уравнение множественной регрессии только со статистически значимыми факторами.
Ранее был сделан вывод о том, что плотность колготок (х1) и фирма-производитель (х2) незначительно влияют на изменение цены (у) продукции. Таким образом, эти факторы можно отбросить.
В п.2. данной работы был проведен анализ коэффициентов корреляции, который показал, что а2 – коэффициент фактора содержания полиамида в составе колготок (х2) – не является статистически значимым. Его также отбрасываем.
Уравнение принимает вид: у = 2,245х3+ 104,163.
Таким образом, наиболее значимым фактором в изменениях цены (у) является содержание лайкры в составе колготок (х3).
4. Отобразить графически исходные данные и расчетные значения.
Для отображения графически исходные значения цены и рассчитанные по модели цены лучше всего использовать Excel (диаграммы).
Похожие работы
... формуле: , где - дополнительная прибыль, полученная от увеличения объема производства и реализации. - дополнительная прибыль, полученная от роста цены реализации. Сд- дополнительные затраты на производство и реализацию продукции, связанные с улучшением качества продукции. Сбр- величина снижения затрат на производство в связи с сокращением количества брака. Годовой экономический эффект от ...
... 85 12 1 36 109,9 20 83 14 1 37 59,9 20 86 14 0 38 79,9 40 82 18 0 39 82,9 20 86 14 0 40 111,8 40 82 18 0 41 83,6 40 82 18 0 42 60 20 86 14 0 43 80 40 82 18 0 44 90 50 76 24 0 45 120 70 74 26 0 Задача состоит в построении линейной модели зависимости цены колготок от их плотности, состава и фирмы-производителя в торговых точках города ...
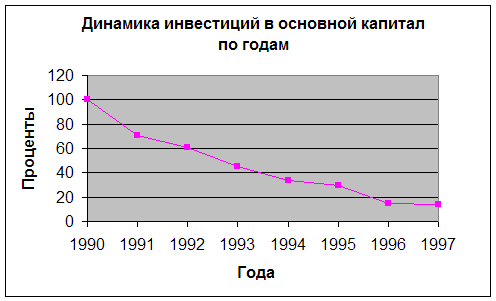
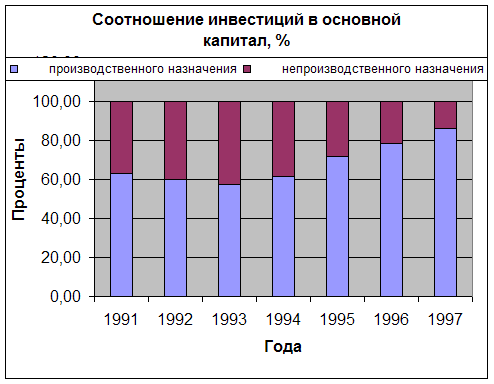
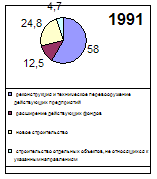
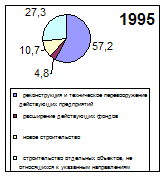
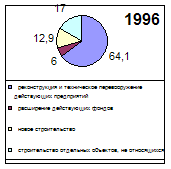
... деревообрабатывающая и целлюлозно-бумажная 96,6 113,3 74,6 47,7 79,9 62,7 71,8 93,9 строительных материалов 135,1 70,7 76,7 39,8 82,3 54,7 79,8 82 пищевая 94,5 90,9 87 99,1 80,5 99,4 86,1 85,2 Выводы по работе. Инвестиции оказывают прямое влияние на качество жизни населения и динамику основных социально-экономических показателей. Динамика инвестиций. ...
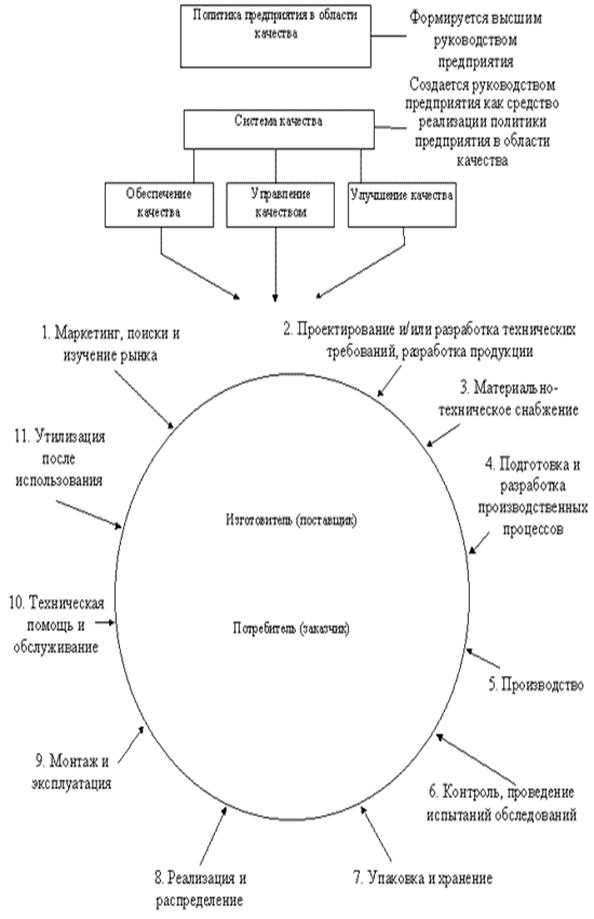
... на основе схем механизмов управления качеством продукции; 2. Современное управление качеством продукции должно прямо ориентироваться на характер потребностей, их структуру и динамику; емкость и конъюнктуру рынка; стимулы, обусловленные экономической и технической конкуренцией, характерные для рыночных отношений; 3. Современное управление качеством на предприятии, независимо от формы ...
0 комментариев