Задача 1
Определить зависимость между фактором и результатирующим признаком по данным, приведенным в таблице. Рассчитать коэффициент корреляции, определить вид зависимости, параметры линии регрессии, корреляционное отношение и оценить точность аппроксимации. Выбор варианта осуществляется по последней цифре порядкового номера студента
Решение:
Построим расчетную таблицу
| N | Расходы по эксплуатации машин и механизмов (тыс. ден. ед), X | Основная заработная плата (тыс. ден. ед), Y | XY | X2 | Y2 |
|
|
|
| 1 | 3,2 | 6,3 | 20,16 | 10,24 | 39,69 | 6,35 | 0,003 | 10,27 |
| 2 | 0,5 | 1,1 | 0,55 | 0,25 | 1,21 | 2,04 | 0,886 | 3,98 |
| 3 | 1,2 | 2,9 | 3,48 | 1,44 | 8,41 | 3,16 | 0,067 | 0,04 |
| 4 | 0,1 | 2,5 | 0,25 | 0,01 | 6,25 | 1,40 | 1,203 | 0,35 |
| 5 | 0,5 | 2,3 | 1,15 | 0,25 | 5,29 | 2,04 | 0,067 | 0,63 |
| 6 | 0,6 | 4,7 | 2,82 | 0,36 | 22,09 | 2,20 | 6,244 | 2,58 |
| 7 | 0,8 | 2,5 | 2 | 0,64 | 6,25 | 2,52 | 0,000 | 0,35 |
| 8 | 1,3 | 3,6 | 4,68 | 1,69 | 12,96 | 3,32 | 0,079 | 0,26 |
| 9 | 2,1 | 5 | 10,5 | 4,41 | 25 | 4,60 | 0,164 | 3,63 |
| 10 | 0,3 | 0,7 | 0,21 | 0,09 | 0,49 | 1,72 | 1,045 | 5,74 |
| 11 | 3,2 | 7 | 22,4 | 10,24 | 49 | 6,35 | 0,421 | 15,25 |
| 12 | 0,5 | 1 | 0,5 | 0,25 | 1 | 2,04 | 1,085 | 4,39 |
| 13 | 1,4 | 3,1 | 4,34 | 1,96 | 9,61 | 3,48 | 0,143 | 0,00 |
| 14 | 1,8 | 2,8 | 5,04 | 3,24 | 7,84 | 4,12 | 1,733 | 0,09 |
| 15 | 0,3 | 1,4 | 0,42 | 0,09 | 1,96 | 1,72 | 0,104 | 2,87 |
| 16 | 0,4 | 1 | 0,4 | 0,16 | 1 | 1,88 | 0,778 | 4,39 |
| 17 | 2,3 | 5,1 | 11,73 | 5,29 | 26,01 | 4,91 | 0,034 | 4,02 |
| 18 | 0,1 | 2,6 | 0,26 | 0,01 | 6,76 | 1,40 | 1,433 | 0,25 |
| 18 | 1,3 | 3,8 | 4,94 | 1,69 | 14,44 | 3,32 | 0,232 | 0,50 |
| 20 | 1,3 | 2,5 | 3,25 | 1,69 | 6,25 | 3,32 | 0,670 | 0,35 |
| сумма | 23,2 | 61,9 | 99,08 | 44 | 251,51 | 61,9 | 16,391 | 59,93 |
| среднее | 3,095 |
Вычислим коэффициент корреляции по формуле:
r ![]()
где X и Y- текущие значения наблюдаемых величин;
N- число наблюдений.
Получим:
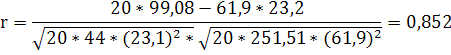
Коэффициент корреляции лежит в пределах 0£ / r /£ 1 . При положительном коэффициенте корреляции наблюдается прямая связь, т.е. с увеличением независимой переменной увеличивается и зависимая.
В нашем примере r = 0,852 ![]() связь тесная
связь тесная
Вычислим уравнение регрессии:
![]()
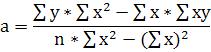
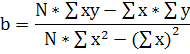
![]()
![]()
![]() - уравнение регрессии
- уравнение регрессии
Построим корреляционное поле
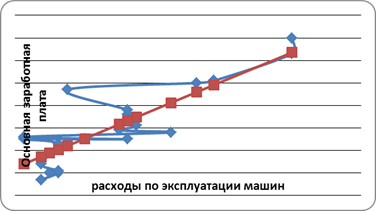
Теснота связи для аппроксимации криволинейных зависимостей определяется при помощи корреляционного отношения
![]()
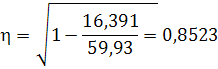
![]() r =
r =![]()
Дополнительной оценкой точности аппроксимации является средняя относительная ошибка аппроксимации. Линия регрессии - аппроксимирующая функция. Чем меньше E, тем точнее выбранная зависимость аппроксимирует существующую зависимость
Вычислим точность аппроксимации:
![]()
где Yi- наблюденное значение зависимой переменной ;
![]() - рассчитанное по формуле значение;
- рассчитанное по формуле значение;
![]() - среднее значение;
- среднее значение;
![]()
Вывод:
1. Между факторами имеется тесная связь.
2. Связь прямая
3. Прямолинейная зависимость лучше отображает связь.
Задача 2
2.1 По приведенным ниже данным – матрицы прибыли в зависимости от выбранной стратегии и состоянии факторов внешней среды, выбрать наиболее предпочтительную стратегию по критериям Лапласа, Вальда, Гурвица и Сэвиджа.
| Состояние факторов внешней среды | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| А | 100 | 120 | 130 | 130 | 120 | 110 |
| Б | 110 | 90 | 150 | 120 | 120 | 100 |
| В | 150 | 150 | 100 | 90 | 100 | 90 |
| Г | 130 | 100 | 110 | 120 | 120 | 110 |
| Д | 150 | 110 | 110 | 100 | 130 | 150 |
| Е | 190 | 90 | 100 | 170 | 120 | 90 |
| Ж | 100 | 140 | 140 | 140 | 130 | 100 |
| З | 120 | 150 | 130 | 130 | 120 | 90 |
| И | 140 | 120 | 130 | 120 | 150 | 100 |
Критерий Лапласа.
Критерием выбора стратегии выступает максимизации математического ожидания.
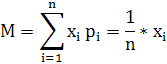
| Состояние факторов внешней среды | М | |||||||
| Варианты стратегий | 1 | 2 | 3 | 4 | 5 | 6 | ||
| А | 100 | 120 | 130 | 130 | 120 | 110 | 118 | |
| Б | 110 | 90 | 150 | 120 | 120 | 100 | 115 | |
| В | 150 | 150 | 100 | 90 | 100 | 90 | 113 | |
| Г | 130 | 100 | 110 | 120 | 120 | 110 | 115 | |
| Д | 150 | 110 | 110 | 100 | 130 | 150 | 125 | |
| Е | 190 | 90 | 100 | 170 | 120 | 90 | 127 | |
| Ж | 100 | 140 | 140 | 140 | 130 | 100 | 125 | |
| З | 120 | 150 | 130 | 130 | 120 | 90 | 123 | |
| И | 140 | 120 | 130 | 120 | 150 | 100 | 127 | |
Вывод: В соответствии с критерием Лапласа стратегии СЕ и СИ характеризуются максимальным математическим ожиданием прибыли.
Критерий Вальда
В соответствии с критерием Вальда субъект, принимающий решение, избирает чистую стратегию, гарантирующую ему наибольший (максимальный) вариант из всех наихудших (минимальных) возможных исходов действия по каждой стратегии. На этой основе получается решение, определяемое как
![]()
| Состояние факторов внешней среды | min | |||||||
| Варианты стратегий | 1 | 2 | 3 | 4 | 5 | 6 | ||
| А | 100 | 120 | 130 | 130 | 120 | 110 | 100 | |
| Б | 110 | 90 | 150 | 120 | 120 | 100 | 90 | |
| В | 150 | 150 | 100 | 90 | 100 | 90 | 90 | |
| Г | 130 | 100 | 110 | 120 | 120 | 110 | 100 | |
| Д | 150 | 110 | 110 | 100 | 130 | 150 | 100 | |
| Е | 190 | 90 | 100 | 170 | 120 | 90 | 90 | |
| Ж | 100 | 140 | 140 | 140 | 130 | 100 | 100 | |
| З | 120 | 150 | 130 | 130 | 120 | 90 | 90 | |
| И | 140 | 120 | 130 | 120 | 150 | 100 | 100 | |
W = 100
Вывод: В соответствии с критерием рекомендуемые стратегии СА, СГ, СД, СЖ, СИ гарантируют максимальный результат (100) в самой неблагоприятной ситуации.
Критерий Гурвица
Согласно критерию Гурвица при выборе решения разумней придерживаться некоторой промежуточной позиции. В соответствии с этим компромиссным критерием для каждого решения определяется линейная комбинация минимального и максимального выигрышей
![]() ,
,
где a- показатель пессимизма-оптимизма, принимающий значения 0£ a£1,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вывод: Согласно критерию Гурвица стратегия СЕ обеспечивает максимальное значение линейной комбинации
Критерий Сэвиджа
Чтобы оценить, насколько то или иное состояние природы влияет на исход в соответствии с критерием Сэвиджа вводится показатель риска(r ij), определяемый как разность между максимально возможным выигрышем при данном состоянии (Rj) и выигрышем при выбранной стратегии (Si)
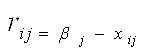 ; при
; при ![]() ,
,
где rij - показатель риска;
bj - максимально возможный выигрыш;
x ij - выигрыш при выбранной стратегии
На этой основе строят матрицу рисков, которая показывает "сожаление между действительным выбором и наиболее благоприятным, если бы были известны намерения природы". Затем выбирается такая стратегия, при которой величина риска принимает минимальное значение в самой неблагоприятной ситуации ![]()
| Без риска | С риском | Без риска | С риском | Без риска | С риском | Без риска | С риском | Без риска | С риском | Без риска | С риском | Max rij | |
| 1 | 2 | 3 | 4 | 5 | 6 | ||||||||
| А | 100 | 90 | 120 | 30 | 130 | 20 | 130 | 40 | 120 | 30 | 110 | 40 | 90 |
| Б | 110 | 80 | 90 | 60 | 150 | 0 | 120 | 50 | 120 | 30 | 100 | 50 | 80 |
| В | 150 | 40 | 150 | 0 | 100 | 50 | 90 | 80 | 100 | 50 | 90 | 60 | 80 |
| Г | 130 | 70 | 100 | 50 | 110 | 40 | 120 | 50 | 120 | 30 | 110 | 40 | 70 |
| Д | 150 | 40 | 110 | 40 | 110 | 40 | 100 | 70 | 130 | 20 | 150 | 0 | 70 |
| Е | 190 | 0 | 90 | 60 | 100 | 50 | 170 | 0 | 120 | 30 | 90 | 40 | 60 |
| Ж | 100 | 90 | 140 | 10 | 140 | 10 | 140 | 50 | 130 | 20 | 100 | 50 | 90 |
| З | 120 | 70 | 150 | 0 | 130 | 20 | 130 | 40 | 120 | 30 | 90 | 60 | 70 |
| И | 140 | 50 | 120 | 30 | 130 | 20 | 120 | 50 | 150 | 0 | 100 | 50 | 50 |
| мах | 190 | 150 | 150 | 170 | 150 | 150 |
S = 50
Вывод: В соответствие с критерием рекомендуемая стратегия СИ, выбирая её в самом худшем случаи наше сожаление не превысит 50.д.ед.
2.2 При заданном распределении состояний факторов внешней среды определить стандартные статистические показатели (среднюю ожидаемую прибыль, дисперсию, коэффициент вариации прибыли) и обосновать выбор стратегии по индивидуальному отношению к риску.
| 0,2 | 0,4 | 0,1 | 0,2 | 0,05 | 0,05 | |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| А | 100 | 120 | 130 | 130 | 120 | 110 |
| Б | 110 | 90 | 150 | 120 | 120 | 100 |
| В | 150 | 150 | 100 | 90 | 100 | 90 |
| Г | 130 | 100 | 110 | 120 | 120 | 110 |
| Д | 150 | 110 | 110 | 100 | 130 | 150 |
| Е | 190 | 90 | 100 | 170 | 120 | 90 |
| Ж | 100 | 140 | 140 | 140 | 130 | 100 |
| З | 120 | 150 | 130 | 130 | 120 | 90 |
| И | 140 | 120 | 130 | 120 | 150 | 100 |
Вычислим среднюю ожидаемую прибыль по формуле:
![]()
МА=100*0,2+120*0,4+130*0,1+130*0,2+120*0,05+110*0,05=118,5
МБ=110*0,2+90*0,4+150*0,1+120*0,2+120*0,05+100*0,05=108
МВ=150*0,2+150*0,4+100*01+90*0,2+100*0,05+90*0,05=127,5
МГ=130*0,2+100*0,4+110*0,1+120*0,2+120*0,05+110*0,05=112,5
МД=150*0,2+110*0,4+110*0,1+100*0,2+100*0,05+150*0,05=119
МЕ=190*0,2+90*0,4+100*0,1+170*0,2+120*0,05+90*0,05=128,5
МЖ=100*0,2+140*0,4+140*0,1+140*0,2+130*0,05+100*0,05=129,5
МЗ=120*0,2+150*0,4+130*0,1+130*0,2+120*0,05+90*0,05=133,5
МИ=140*0,2+120*0,4+130*0,1+120*0,2+150*0,05+100*0,05=125,5
Вычислим среднее квадратичное (стандартное) отклонение:
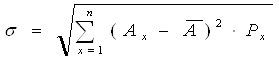
где s - стандартное отклонение;
Ax - результат для вероятности Px;
a - среднее ожидаемое значение результата;
Px - вероятность появления этого результата
![]()
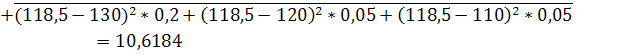
![]()
![]()
![]()
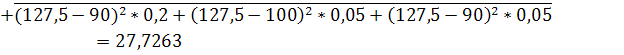
![]()
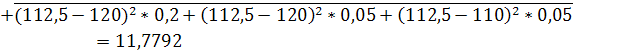
![]()
![]()
![]()
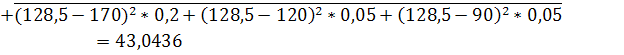
![]()
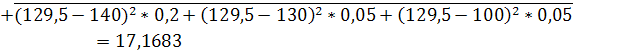
![]()
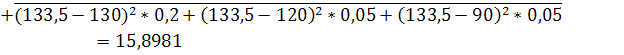
![]()
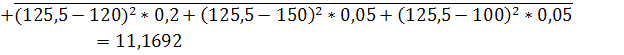
Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:
![]() ,
,
где ![]() - искомый показатель,
- искомый показатель, ![]() - среднее квадратичное отклонение,
- среднее квадратичное отклонение, ![]() - средняя величина.
- средняя величина.
| 1 | 2 | 3 | 4 | 5 | 6 | м | |
| А | 100 | 120 | 130 | 130 | 120 | 110 | 118,5 |
| Б | 110 | 90 | 150 | 120 | 120 | 100 | 108 |
| В | 150 | 150 | 100 | 90 | 100 | 90 | 127,5 |
| Г | 130 | 100 | 110 | 120 | 120 | 110 | 112,5 |
| Д | 150 | 110 | 110 | 100 | 130 | 150 | 119 |
| Е | 190 | 90 | 100 | 170 | 120 | 90 | 128,5 |
| Ж | 100 | 140 | 140 | 140 | 130 | 100 | 129,5 |
| З | 120 | 150 | 130 | 130 | 120 | 90 | 133,5 |
| И | 140 | 120 | 130 | 120 | 150 | 100 | 125,5 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Чем больше значение коэффициента вариации, тем относительно больший разброс и меньшая выравненность исследуемых значений. Если коэффициент вариации меньше 10%, то изменчивость вариационного ряда принято считать незначительной, от 10% до 20% относится к средней, больше 20% и меньше 33% к значительной и если коэффициент вариации превышает 33%, то это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.
Построим таблицу
| 1 | 2 | 3 | 4 | 5 | 6 | м |
| [М- | V% | |
| А | 100 | 120 | 130 | 130 | 120 | 110 | 118,5 | 10,61838 | [107,88 ;129,12] | 8,95 |
| Б | 110 | 90 | 150 | 120 | 120 | 100 | 108 | 18,60108 | [89,40 ;126,60] | 17,22 |
| В | 150 | 150 | 100 | 90 | 100 | 90 | 127,5 | 27,72634 | [99,77 ;155,23] | 21,74 |
| Г | 130 | 100 | 110 | 120 | 120 | 110 | 112,5 | 11,77922 | [100,72; 124,28] | 10,46 |
| Д | 150 | 110 | 110 | 100 | 130 | 150 | 119 | 18,9473 | [100,05 ;137,95] | 15,92 |
| Е | 190 | 90 | 100 | 170 | 120 | 90 | 128,5 | 43,04358 | [85,46 ;171,54] | 33,49 |
| Ж | 100 | 140 | 140 | 140 | 130 | 100 | 129,5 | 17,16828 | [112,33 ;146,67] | 13,25 |
| З | 120 | 150 | 130 | 130 | 120 | 90 | 133,5 | 15,89811 | [117,60 ;149,40] | 11,9 |
| И | 140 | 120 | 130 | 120 | 150 | 100 | 125,5 | 11,16915 | [114,33 ;136,67] | 8,9 |
Вывод: на мой взгляд самая оптимальная стратегия СЕ, т.к во время кризиса мы потеряем много прибыли, но в тоже время в благоприятных условиях мы приобретем много прибыли.
Похожие работы
... математической статистики. Если в собранных эмпирических материалах (анкетах, результатах экспериментов) проявляется действие статистических закономерностей, то применение методов теории вероятностей и математической статистики в конкретном социально-правовом исследовании для анализа и обработки полученных материалов не только желательно, но и необходимо. Для социологии права значительный интерес ...
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
... понятие теории понятие множества не подлежит логическому определению. Элементы множества могут иметь самую различную природу. Например, можно говорить о множестве микросхем, входящих в определенную конструкцию РЭА, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия, и т. д. Множества обозначают заглавными буквами латинского ...
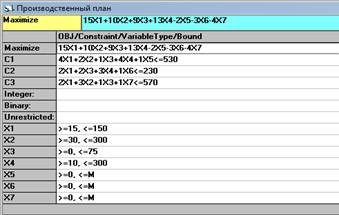
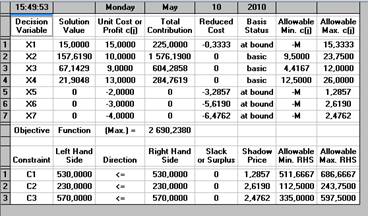
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
0 комментариев