Навигация
Экономико-математические методы и модели
Экономико-математические методы и модели
Методически указания и контрольные задания для студентов
очной и заочной формы обучения.
г. Ставрополь 2007г.
Настоящее пособие предназначено для студентов экономических специальностей. Учебный план изучения курса рассчитан на 75 часов и предусматривает выполнение контрольной работы для заочной формы обучения.
В пособии приведены решения задач по темам, соответствующим учебному плану, даны необходимые методические указания и приведены задания для контрольной работы. Это пособие может быть использовано студентами очного и заочного отделения для самостоятельной работы и подготовки к зачёту.
Введение
В настоящее время процессы принятия решений в экономике опираются на достаточно широкий круг экономико-математических методов и моделей. Ни одно серьёзное решение, затрагивающее управление деятельностью отраслей и предприятий, распределения ресурсов, изучение рыночной конъюнктуры, прогнозирование, планирование и т.п., не осуществляется без предварительного математического исследования конкретного процесса или его частей.
В этой связи изучение дисциплины «Экономико-математические методы и модели» направлено как на формирование у студентов понимания роли современной математики в экономике, так и на изучение наиболее важных экономико-математических методов исследования моделей и задач оптимизации.
Задачи данной дисциплины состоят в изучении математических методов СЭП, применения базовых методов математического моделирования СЭП при решении оптимизационных задач и выработке навыков решения трудоёмких прикладных экономико-математических задач с помощью компьютерных технологий.
Цель изучения данной дисциплины – подготовка специалиста экономического профиля к сознательному использованию математических методов исследования СЭП на основе соответствующих базовых моделей.
Изучение дисциплины предусматривает сочетание лекций, практических занятий и самостоятельную работу студентов. На лекциях излагается содержание дисциплины, проводится анализ основных математических понятий и методов. Практические занятия ориентированны на выработку у студентов умения и навыков решения типовых экономических задач. Руководствуясь принципом повышения уровня фундаментальной математической подготовки студентов с усилением её прикладной экономической направленности, автором предлагаются наиболее экономически значимые задачи, представляющие самостоятельный интерес и дающие возможность относительно продуктивно освоить алгоритм их решения при отсутствии учебника.
После изучения дисциплины «Экономико-математические методы и модели» студент должен:
- иметь представление о методах системного анализа и управления СЭП;
- знать основные понятия, определения и базовые математические методы, используемые для построения моделей СЭП;
- уметь проводить расчёты и делать оценки параметров для базовых математических моделей СЭП;
- уметь решать прикладные экономико-математические задачи, опираясь на базовые знания по математике, соответствующие Государственному образовательному стандарту.
Общие методические указания
Для более полного, уверенного освоения студентами навыков решения задач по дисциплине «Экономико-математические методы и модели» предлагаются данные методические указания. Автор руководствовался общими целеполагающими принципами изучения данной дисциплины, а также принципом повышения уровня фундаментальной математической подготовки студентов для понимания значимости построения и исследования математических моделей в экономике.
Приведённые методические указания могут быть использованы при проведении самостоятельных и контрольных работ, собеседований при сдаче зачёта.
При выполнении контрольной работы студентам заочного отделения необходимо руководствоваться следующими указаниями:
- на обложке указываются фамилия и инициалы студента, полный шифр специальности, группа, дата регистрации, фамилия и инициалы преподавателя-рецензента;
- решение всех задач и пояснения к ним должны быть достаточно подробными; вычисления и чертежи – полными и аккуратными.
- для удобства рецензирования рекомендуется оставлять поля;
- номер контрольной работы соответствует последней цифре его учебного шифра.
Контрольная работа предоставляется в деканат не позднее 10 дней до начала сессии. При сдаче зачёта студент должен дать пояснения к решённым заданиям.
Рекомендуемая литература:
1. Исследование операций в экономике: Учеб. пособ. / под ред. Н.Ш.Кремера./ – М.: ЮНИТИ, 2000. - 407 с.
2. Практикум по высшей математике для экономистов: Учеб. пособие для вузов / Кремер Н.Ш. и др.; под ред. проф. Н.Ш.Кремера – М.: ЮНИТИ – ДАНА, 2005. – 423 с.
3. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособ. М..: Высшая школа, 1986. - 319 с.
4. Морозов В.В., Сухарев А.Т., Фёдоров В.В. Исследование операций в примерах и задачах.: Учеб. пособие. М.: Высшая школа, 1986. – 287 с.
5. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. Учеб. пособие для студентов втузов. – М.: Высшая школа, 2001. – 208 с.
6. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с.
7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с.
8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. -391 с.
Глоссарий терминов.
Аддитивность - свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части. Характеристика системы аддитивна, если она равна сумме тех же характеристик для всех составляющих систему подсистем и элементов.
Адекватность модели - ее соответствие моделируемому объекту или процессу. При моделировании имеется в виду адекватность не вообще, а по тем свойствам модели, которые для исследования считаются существенными.
Аппроксимация - приближенное выражение сложной функции с помощью более простых, что часто значительно упрощает решение задачи.
Вариантные прогнозы - прогнозы, основанные на сопоставлении различных вариантов возможного развития экономики при разных предположениях относительно того, как будет развиваться техника, какие будут приниматься экономические меры и т. д.
Векторная оптимизация - решение задач математического программирования, в которых критерий оптимальности представляет собой вектор, компонентами которого являются в свою очередь различные несводимые друг к другу критерии оптимальности подсистем, входящих в данную систему, например критерии разных социальных групп в социально-экономическом планировании.
Верификация имитационной модели - проверка соответствия ее поведения предположениям экспериментатора.
Вероятностная модель - модель, которая в отличие от детерминированной модели содержит случайные элементы. Таким образом, при задании на входе модели некоторой совокупности значений, на ёе выходе могут получаться различающиеся между собой результаты в зависимости от действия случайного фактора.
Взаимозаменяемость ресурсов — возможность использования разных ресурсов для достижения оптимума. Именно этим обусловлена проблема выбора: там, где нет заменяемости, нет и выбора, и тогда фундаментальное понятие оптимальности теряет смысл.
Генетический прогноз («поисковый») — прогноз, показывающий, к каким состояниям придет прогнозируемый объект в заданное время при определенных начальных условиях.
Глобальное моделирование или моделирование глобального развития — область исследований, посвященная разработке моделей наиболее масштабных социальных, экономических и экологических процессов, охватывающих земной шар.
Градиентные методы решения задач математического программирования - методы, основанные на поиске экстремума (максимума или минимума) функции путем последовательного перехода к нему с помощью градиента этой функции.
Декомпозиционные методы решения оптимальных задач - основанные на рациональном расчленении сложной задачи и решении отдельных подзадач с последующим согласованием частых решений для получения общего оптимального решения.
Дескриптивная модель - модель, предназначенная для описания и объяснения наблюдаемых фактов или прогноза поведения объектов - в отличие от нормативных моделей, предназначенных для нахождения желательного состояния объекта (например, оптимального).
Детерминированная модель - аналитическое представление закономерности, операции и т. п., при которых для данной совокупности входных значений на выходе системы может быть получен единственный результат. Такая модель может отображать как вероятностную систему (тогда она является некоторым ее упрощением), так и детерминированную систему.
Детерминированная система - такая система, выходы которой (результаты действия, конечные состояния и т.п.) однозначно определяются оказанными на нее управляющими воздействиями.
Динамическая система - всякая система, которая изменяется во времени (в отличие от статической системы). Математически это принято выражать через переменные (координаты), изменяющиеся во времени. Процесс изменения характеризуется траекторией (т. е. наборами координат, каждая из которых является функцией времени).
Динамические модели межотраслевого баланса - частный случай динамических моделей экономики, основаны на принципе межотраслевого баланса, в который дополнительно вводятся уравнения, характеризующие изменения отраслевых связей во времени.
Итеративные (итерационные) методы решения задач - заключаются в том, что вычислительный процесс начинают с некоторого пробного (произвольного) допустимого решения, а затем применяют алгоритм, обеспечивающий последовательное улучшение этого решения.
Итерация - повторное применение математической операции (с измененными данными) при решении вычислительных задач для постепенною приближения к нужному результату. Итеративные расчеты на ЭВМ характерны для решения экономических (особенно оптимизационных и балансовых) задач. Чем меньше требуется пересчетов, тем быстрее сходится алгоритм.
Коэффициенты прямых затрат (технологические коэффициенты) в межотраслевом балансе - средние величины непосредственных затрат продукции одной отрасли (в качестве средств производства) на выпуск единицы продукции другой отрасли. Они могут быть выражены в натуральной форме (кВт/ч и т. д.) или стоимостной (руб.).
Критерий оптимальности - показатель, выражающий меру экономического эффекта принимаемого хозяйственного решения для сравнительной оценки возможных решений (альтернатив) и выбора наилучшего из них (например, максимум прибыли, минимум трудовых затрат, кратчайшее время достижения цели и т. д.)
Коэффициенты полных материальных затрат в межотраслевом балансе - средние затраты i-го продукта на производство конечного продукта j по всей цепи сопряженных производств. Таким образом, они складываются из прямых затрат каждой отрасли на данный продукт и косвенных затрат.
Коэффициенты прямых затрат (технологические коэффициенты) в межотраслевом балансе - средние величины непосредственных затрат продукции одной отрасли (в качестве средств производства) на выпуск единицы продукции другой отрасли. Они могут быть выражены в натуральной форме (кВт/ч и т. д.) или стоимостной (руб.).
Математическое программирование (оптимальное программирование) — область математики, объединяющая различные математические методы и дисциплины: линейное программирование, нелинейное программирование, динамическое программирование, выпуклое программирование и др. Общая задача математического программирования состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.
Матричные модели - модели, построенные в виде таблиц (матриц). Они отображают соотношения между затратами на производство и его результатами, нормативы затрат, производственную и экономическую структуру хозяйства. Применяются в межотраслевом балансе, матричном плане предприятия и др.
Машинная имитация - экспериментальный метод изучения объекта с помощью электронных вычислительных машин, Процесс имитации заключается в следующем: сначала строится математическая модель изучаемого объекта (имитационная модель), затем эта модель преобразуется в программу работы ЭВМ.
Межотраслевой баланс (МОБ) - каркасная модель экономики, таблица, в которой показываются многообразные натуральные и стоимостные связи в народном хозяйстве. Анализ МОБ дает комплексную характеристику процесса формирования и использования совокупного общественного продукта в отраслевом разрезе.
Объективно обусловленные (оптимальные) оценки - одно из основных понятий линейного программирования. Это оценки продуктов, ресурсов, работ, вытекающие из условий решаемой оптимизационной задачи. Их называют также двойственными оценками, разрешающими множителями, множителями Лагранжа и целым рядом других терминов.
Ограничения модели - запись условий, в которых действительны расчеты, использующие эту модель. Обычно представляя собою систему уравнений и неравенств, они в совокупности определяют область допустимых решений (допустимое множество). Распространены линейные и нелинейные ограничения (на графике первые изображаются прямыми, вторые — кривыми линиями).
Определенность в системе - ситуация, когда имеется точная информация о возможных состояниях системы в случае принятия тех или иных решений.
Оптимальное планирование - комплекс методов, позволяющих выбрать из многих возможных (альтернативных) вариантов плана или программы один оптимальный вариант, т. е. наилучший с точки зрения заданного критерия оптимальности и определенных ограничений.
Оптимальное программирование - применение в экономике методов математического программирования.
Оптимальное управление - основное понятие математической теории оптимальных процессов (принадлежащей разделу математики под тем же названием: оптимальное управление); означает выбор таких управляющих параметров, которые обеспечивали бы наилучшее, с точки зрения заданного критерия, протекание процесса, или, иначе, наилучшее поведение системы, ее развитие к цели по оптимальной траектории.
Оптимизационная задача - экономико-математическая задача, цель которой состоит в нахождении наилучшего (с точки зрения какого-то критерия) распределения наличных ресурсов. Решается с помощью оптимизационной модели методами математического программирования.
Оптимизация - 1) процесс нахождения экстремума функции, т. е. выбор наилучшего варианта из множества возможных; 2) процесс приведения системы в наилучшее (оптимальное) состояние. Очередь — в теории массового обслуживания — последовательность требований или заявок, которые, заставая систему обслуживания занятой, не выбывают, а ожидают ее освобождения (затем они обслуживаются в том или ином порядке). Очередью можно назвать также и совокупность ожидающих (простаивающих) каналов или средств обслуживания.
Пассивный (безусловный) статистический прогноз - прогноз развития, основанный на изучении статистических данных за прошлый период и переносе выявленных закономерностей на будущее. При этом внешние факторы, воздействующие на систему, принимаются неизменными и считается, что ее развитие основывается только на собственных, внутренних тенденциях.
Предельные и приростные величины в экономике. Предельная величина характеризует не состояние (как суммарная или средняя величины), а процесс, изменение. Поскольку в экономике большинство процессов (например, рост производства или изменение его эффективности) являются функциями ряда аргументов (факторов), то предельные величины здесь обычно выступают как частные производные процесса по каждому из факторов.
Прогнозирование - система научных исследований качественного и количественного характера, направленных на выяснение тенденций развития народного хозяйства и поиск оптимальных путей достижения целей этого развития.
Прогнозирование спроса - исследование будущего (возможного) спроса на товары и услуги в целях лучшего обоснования соответствующих производственных планов. Прогнозирование подразделяется на краткосрочное (конъюнктурное), среднесрочное и долгосрочное.
Производственная функция - экономико-математическое уравнение, связывающее переменные величины затрат (ресурсов) с величинами продукции (выпуска). Математически производственные функции (ПФ) могут быть представлены в различных формах — от столь простых, как линейная зависимость результата производства от одного исследуемого фактора, до весьма сложных систем уравнений, включающих рекуррентные соотношения, которыми связываются состояния изучаемого объекта в разные периоды времени. Широко распространены мультипликативные формы ПФ.
Равновесие - состояние экономической системы, которое характеризуется равенством спроса и предложения всех ресурсов.
Регрессия - зависимость среднего значения какой-либо случайной величины от некоторой другой величины или нескольких величин. Распределение этих значений называется условным распределением у при данном х. Множественная регрессия в определенных условиях позволяет исследовать влияние причинных факторов.
Рекурсия - в общем смысле вычисление функции по определенному алгоритму. Примерами таких алгоритмов являются рекуррентные формулы, выводящие вычисление заданного члена последовательности (чаще всего числовой) из вычисления нескольких предыдущих ее членов.
Статистическое моделирование - способ исследования процессов повеления вероятностных систем в условиях, когда неизвестны внутренние взаимодействия в этих системах.
Стохастическая имитация — вид машинной имитации, отличающийся от детерминированной тем, что включает в модель в том или ином виде случайные возмущения, отражающие вероятностный характер моделируемой системы.
Устойчивость решения — обычно, говоря об устойчивости решения задачи, имеют в виду, что малые изменения каких-либо характеристик, например, начальных условий, ограничений или целевого функционала, не приводят к качественному изменению решения.
Целевая функция в экстремальных задачах - функция, минимум или максимум которой нужно найти. Это ключевое понятие оптимального программирования. Найдя экстремум целевой функции и, следовательно, определив значения управляемых переменных, которые k нему приводят, мы тем самым находим оптимальное решение задачи.
Шкалы — системы чисел или иных элементов, принятых для оценки или измерения каких-либо величин. Шкалы используются для оценки и выявления связей и отношений между элементами систем. Особенно широко их применение для оценки величин, выступающих в роли критериев качества функционирования систем, в частности, критериев оптимальности при решении экономико-математических задач.
Практическое занятие.
Тема. Методы линейной алгебры в экономическом анализе.
Цель. Решение экономических задач с элементами моделирования, опирающиеся на базовую основу линейной алгебры.
Похожие работы
... системы цен по остальным товарам. Конец XIX – начало XX века ознаменовались широким использованием математики в экономике. В XX в. математические методы моделирования используются столь широко, что почти все работы, удостоенные Нобелевской премии по экономике, связаны с их применением (Д. Хикс, Р. Солоу, В. Леонтьев, П. Самуэльсон, Л. Канторович и др.). Развитие предметных дисциплин в большинстве ...
... моделей экстремальных планов и экстремальных значений целевой функции быть не может. Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение. Методика построения экономико-математической модели состоит в том, чтобы ...
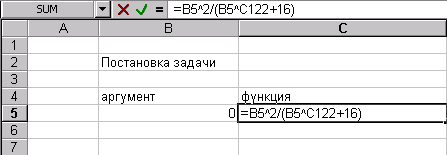
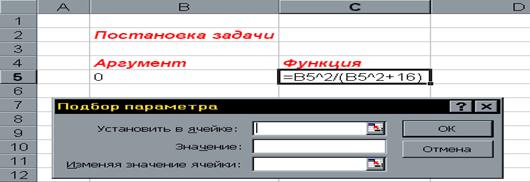
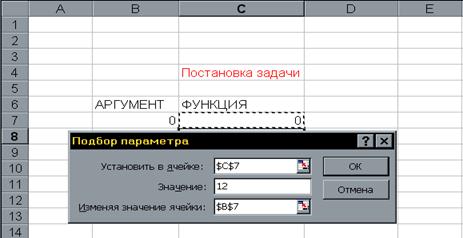
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...


0 комментариев