Навигация
Определим матрицу коэффициентов полных материальных затрат с помощью формул обращения невыраженных матриц (первый способ)
3. определим матрицу коэффициентов полных материальных затрат с помощью формул обращения невыраженных матриц (первый способ).
А) находим матрицу (Е - А):
![]()
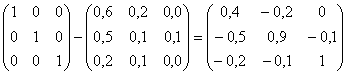
Б) вычисляем определитель этой матрицы:
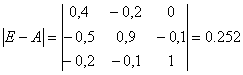
В) транспонируем матрицу (Е - А):
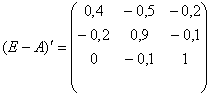
Г) находим алгебраические дополнения для элемента матрицы ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, присоединенная к матрице (Е – А) матрица имеет вид:
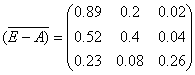
Д) используя формулу (7.14), находим матрицу коэффициентов полных материальных затрат:
![]()

Элементы матрицы В, рассчитанные по точным формулам обращения матриц, больше соответствующих элементов матрицы, рассчитанных по второму приближенному способу без учета косвенных материальных затрат порядка выше 2-го.
1. найдем величины валовой продукции трех отраслей (вектор Х), используя формулу (7.9)
![]()
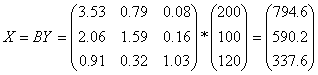
2. для определения элементов первого квадрата материального межотраслевого баланса воспользуемся формулой, вытекающей из формулы (7.4): ![]() . Из этой формулы следует, что для получения первого столбца первого квадрата нужно элементы первого столбца заданной матрицы А умножить на величину
. Из этой формулы следует, что для получения первого столбца первого квадрата нужно элементы первого столбца заданной матрицы А умножить на величину ![]() ; элементы второго столбца матрицы А умножить на
; элементы второго столбца матрицы А умножить на ![]() ; элементы третьего столбца матрицы А умножить на
; элементы третьего столбца матрицы А умножить на ![]() .
.
Составляющие третьего квадранта (условно чистая продукция) находятся с учетом формулы (7.1) как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.
Четвертый квадрант в нашем примере состоит из одного показателя и служит, в частности, для контроля правильности расчета: сумма элементов второго квадранта должна в стоимостном материальном балансе совпадать с суммой элементов третьего квадранта. Результаты расчета приведены в таблице.
| Производящие отрасли | Потребляющие отрасли | ||||
| 1 | 2 | 3 | Конечная продукция | Валовая продукция | |
| 1 2 3 | 476.76 397.3 158.92 | 118.04 59.02 59.02 | 0 33.76 0 | 200 100 120 | 794.6 590.2 337.6 |
| Условно чистая продукция | -238.38 | 354.12 | 303.84 | 420 | |
| Валовая продукция | 794.6 | 590.2 | 337.6 | 1722.4 | |
Задание 5
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящей средней с интервалом сглаживания 3, методом экспоненциального сглаживания (![]() =0,1), представить результаты сглаживания графически, определите для ряда трендовую модель в виде полинома первой степени (линейную модель), дайте точечный и интервальный прогноз на три шага вперед.
=0,1), представить результаты сглаживания графически, определите для ряда трендовую модель в виде полинома первой степени (линейную модель), дайте точечный и интервальный прогноз на три шага вперед.
| Вариант | Ряд данных |
| 1 | у = 12, 10, 11, 13, 14, 15, 14, 13, 15, 16 |
Найдем среднее арифметическое ![]()
Среднее квадратическое отклонение ![]()
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| - | 1.06 | 0.53 | 1,06 | 0.53 | 0.53 | 0.53 | 0.53 | 1.06 | 0.53 |
Аномальный уровень отсутствует.
Методом простой скользящей средней с интервалом сглаживания 3
Для вычисления сглаженных уровней ряда ![]() применяется формула:
применяется формула:

где ![]() при нечетном m, в нашем случае m = 3, следовательно
при нечетном m, в нашем случае m = 3, следовательно ![]()
| y(t) | 12 | 10 | 11 | 13 | 14 | 15 | 14 | 13 | 15 | 16 |
|
| - | - | 11 | 11.3 | 12.7 | 14 | 14.3 | 14 | 14 | 14.7 |
Методом экспоненциального сглаживания (![]() =0,1)
=0,1)
Экспоненциальное сглаживание осуществляется по формуле:![]() , где
, где ![]() - параметр сглаживания. В нашем случае
- параметр сглаживания. В нашем случае ![]() = 0,1.
= 0,1.
![]()
| y(t) | 12 | 10 | 11 | 13 | 14 | 15 | 14 | 13 | 15 | 16 |
|
| 11.1 | 10.99 | 2.2 | 3.28 | 4.35 | 5.42 | 6.29 | 6.96 | 7.76 | 8.58 |
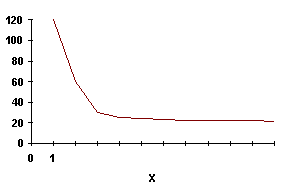
Графическое представление результатов сглажевания
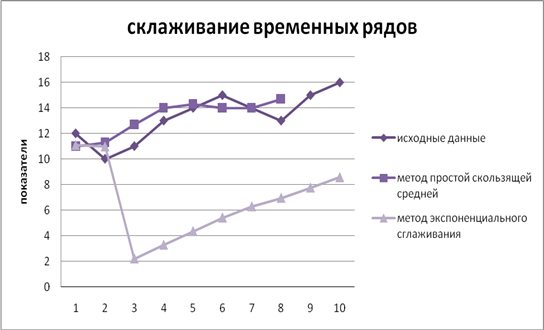
Ниже в таблице приведены исходный ряд данных yt и сглаженные двумя способами уровни исходного ряда. При этом при сглаживании при помощи метода простой скользящей средней использовался интервал сглаживания m = 3.
При сглаживании экспоненциальным методом был доведён параметр сглаживания а = 0,1
Соответственно, числовая последовательность весов имела вид:
| t | yt
|
простой скользящей средней | _ методом y экспоненциального сглаживания |
| 1 | 12 | - | 11.1 |
| 2 | 10 | 11 | 10.99 |
| 3 | 11 | 11.3 | 2.2 |
| 4 | 13 | 12.7 | 3.28 |
| 5 | 14 | 14 | 4.35 |
| 6 | 15 | 14.3 | 5.42 |
| 7 | 14 | 14 | 6.29 |
| 8 | 13 | 14 | 6.96 |
| 9 | 15 | 14.7 | 7.76 |
| 10 | 16 | - | 8.58 |
Чтобы правильно подобрать лучшую кривую роста для моделирования и прогнозирования экономического явления, необходимо знать особенности каждого вида кривых в экономике часто используется полиномиальная кривая роста, как кривая с полиномом первой степени.
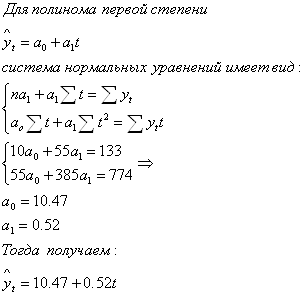
Параметр a1 называют линейным приростом. Для полинома первой степени характерен постоянный закон роста. Если посчитать первые приросты по формуле
ut = yt – yt-1, t = 2,3,…,n,
то они будут постоянной величиной и равны а 1.
Значения прироста для полиномов любого порядка не зависят от значений самой функции ![]() .
.
Полиномные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня. Исходный временной ряд предварительно сглаживается методом простой скользящей средней.
Необходимо оценить адекватность и точность построения модели, т.е. необходимо выполнение следующих условий:
a) проверка случайности колебаний уровней остаточной последовательности:
![]()
Проверку случайности уровней ряда проведем по критерию пиков, должно выполняться:![]()

| t | Фактическое | Расчётное | Отклонение | Точки пиков |
| 1 2 3 4 5 6 7 8 9 10 | 12 10 11 13 14 15 14 13 15 16 | 10.99 11.51 12.03 12.55 13.07 13.59 14.11 14.63 15.15 15.67 | 1.01 -1.51 -1.03 0.45 0.93 1.41 -0.11 -1.63 -0.15 0.33 | -- 1 0 0 0 1 0 1 0 - |
| 55 | 133 | 133.3 | - | 3 |
a) проверка соответствия распределения случайной компоненты нормальному закону распределения:

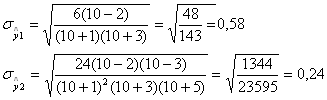
В соответствии с характером изменения средних приростов и производных показателей выбирается вид кривой роста для исходного временного ряда.
Необходимые условия:
![]()
Если эти условия выполняются одновременно, то гипотеза о характере распределения случайной компоненты принимается, если выполняется хотя бы одно из следующих неравенств:
![]()
то гипотеза о нормальном распределении отвергается, трендовая модель признаётся неадекватной.
1) ![]()
2) ![]()
Таким образом, одно из неравенств не выполняется, трендовая модель неадекватна, значит, дальнейшее исследование не имеет смысла, но попробуем.
Прогнозирование экономических показателей на основе трендовых моделей основано на распространении закономерностей, связей и соотношений, действующих в изучаемом периоде, за его пределами. Достоверный прогноз возможен лишь относительно таких объектов и явлений, которые в значительной степени детерминируются прошлым и настоящим. При прогнозировании лучше задавать интервалы значений, в которых с достаточной долей уверенности можно ожидать появления прогнозируемой величины. Установление такого интервала называется интервальным прогнозом.
Прогноз на основании трендовых моделей (кривых роста) содержит два элемента: точечный и интервальный прогнозы.
Для полинома первой степени адекватная линейная модель
![]()
![]() = 10.47 + 0,52t
= 10.47 + 0,52t
Получим точечные прогнозы, подставляя в формулу
![]() = а0 + а1t
= а0 + а1t
значения t = 11, t=12, t =13, то есть на три шага вперёд.
Среднее значение по ряду было определено ранее ,это число11
a 1 для полинома первой степени выведено и равно 0,52
![]() 11 = 11 + 0,52 * 11 = 16.72
11 = 11 + 0,52 * 11 = 16.72
![]() 12 = 11+ 0,52 * 12 = 17.24
12 = 11+ 0,52 * 12 = 17.24
![]() 13 = 11 + 0,52* 13 = 17.76
13 = 11 + 0,52* 13 = 17.76
Вычислим значения величины К путём их линейной экстраполяции приведённых имеющихся значений для числа уровней в ряду n = 11, 12, 13.
По таблице значений величина К для t = 10 (L = 1) K = 1,77
Для t = 11 (L= 1) K = 1,88
Для t = 12 (L= 2) K = 1,73
Для t = 13 (L= 3) K = 1,68
Определим среднюю квадратическую ошибку прогнозируемого показателя
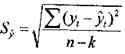 10.41/10 –1,77=1,26 корень=1.12
10.41/10 –1,77=1,26 корень=1.12
Для n 11 K после расчёта по формуле = 0.15
Для n 12 К = 0.19
Для n 13 К = 0.23
Интервальный прогноз на базе трендовых моделей осуществляется путём расчёта доверительного интервала. В этом интервале учитывается верхняя и нижняя границы
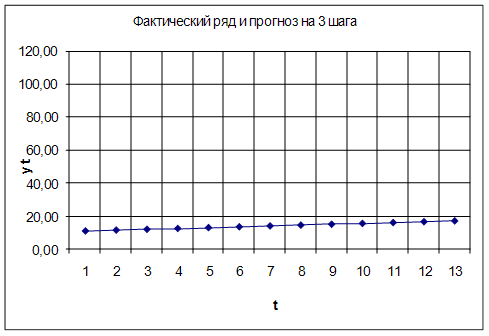
| Время t | Шаг L | Точечный прогноз | Доверительный интервал прoгноза | |
| Нижняя граница | Верхняя граница | |||
| 11 12 13 | 1 2 3 | 16.72 17.24 17.76 | 15.83 17.02 17.5 | 16.88 17.45 18.02 |
![]() Ввиду того, что предыдущая трендовая модель неадекватна выясним по формуле среднюю относительную ошибку аппроксимации по формуле:
Ввиду того, что предыдущая трендовая модель неадекватна выясним по формуле среднюю относительную ошибку аппроксимации по формуле:
![]()
а.) для трендовой модели по методу простой скользящей средней:
(1 : 8) * (0 + 0,13+ 0,09+ 0,07 +(-0,02) + (-0,08) + 0,07 +0,08)* 100%= 42.5%
б) для трендовой модели по экспоненциальному способу:
( 1 : 10) * (0,08+ (-0,099) +0,8 +0,75 +0,69 +0,64 +0,55 +0,46 +0,48 +
0,46)* 100% = 48.11%
Можно выбрать для прогноза трендовую модель по экспоненциальному способу, как наиболее точную.
Задание 6
Пункт по ремонту радиотехники работает в режиме отказа с одним мастером. Интенсивность потока заявок ![]() , производительность мастера
, производительность мастера ![]() . Определить предельные значения относительной пропускной способности Q, абсолютной пропускной способности А и вероятность отказа
. Определить предельные значения относительной пропускной способности Q, абсолютной пропускной способности А и вероятность отказа ![]() телефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят.
телефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят.
| Вариант | Интенсивность потока заявок | Интенсивность потока обслуживания |
| 1 | 0.25 | 0.35 |
Решение.
Так как пункт по ремонту радиотехники является СМО с отказами, характеризующаяся параметрами: интенсивность потока заявок ![]() =0.25 и Интенсивность потока обслуживания
=0.25 и Интенсивность потока обслуживания ![]() , то по формуле определим предельную вероятность отказа:
, то по формуле определим предельную вероятность отказа:
![]()
или 41%, т.е. в установившемся режиме из каждых 100 заявок в среднем 41 получают отказ.
Определим предельное значение относительной Q и абсолютной A пропускной способности СМО:
![]()
Итак, из расчета следует, что случайный характер поступления телефонных вызовов и случайных характер длительности разговоров порождают ситуацию, что абсолютная пропускная способность А = 0,148 разговора/мин более чем в два раза меньше производительности телефонной линии ![]() вызовов/ мин.
вызовов/ мин.
Определим далее:
Ø среднее время обслуживания ![]() мин.
мин.
Ø среднее время простоя канала ![]() мин.
мин.
Ø Вероятность того, что канал свободен 
или ![]()
Ø Вероятность того, что канал занят ![]()
Таким образом, вероятность того, что канал занят, меньше вероятности того, что канал свободен, и этого следовало ожидать, так как интенсивность входящего потока ![]() меньше интенсивности производительности канала
меньше интенсивности производительности канала ![]() .
.
Похожие работы
... количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна. Математическая модель Обозначим x1, x2, x3, x4 количества продуктов П1, П2, П3, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать, — стоимость рациона (обозначим её L): она линейно зависит от элементов ...
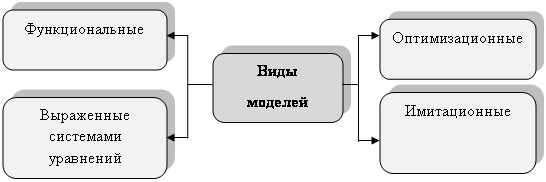
... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...
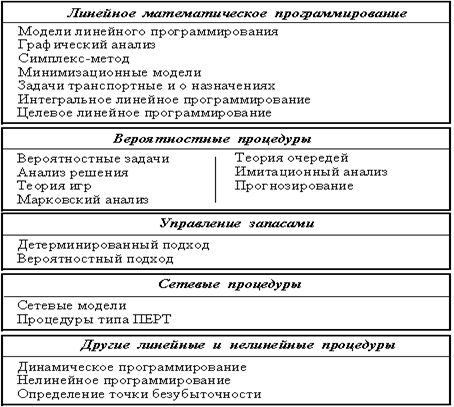
... Теория очередей 59,7 Нелинейное программирование 46,8 Динамическое программирование 38,7 Теория игр 30,6 Следует отметить определенную переоценку значимости экономико-математических моделей в реальной практике управления экономико-производственными системами. Это связано с непреодолимыми пока сложностями моделирования процессов в экономико-производственных системах из-за непрерывности ...
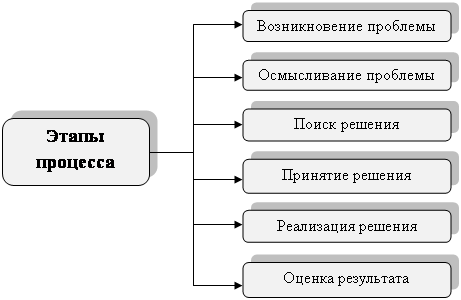
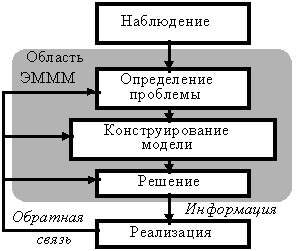
... заданное его качество, определение оптимальных (с точки зрения принятого критерия) норм дежурного обслуживания, надобность в котором возникает непланомерно, нерегулярно. С использованием метода математического моделирования можно определить, например, оптимальное количество автоматически действующих машин, которое может обслуживаться одним рабочим или бригадой рабочих и т.п. Типичным примером ...


0 комментариев