Навигация
Поширення світла в ізотопних середовищах
1. Поширення світла в ізотопних середовищах
1.1 Відбивання світла
Обладнання: набір по геометричній оптиці, оптична шайба, випрямляч ВС-24 або ВС 4-12.
Приступаючи до демонстрації дослідів з використанням оптичної шайби, слід відрегулювати освітлення екрана. Необхідно добитись такого положення освітлювача, щоб по всій довжині екрана проходили яскраві і чітко видимі смужки світла щоб при обертанні освітлювача навколо шайби промені не затемнювались.
Освітлювач (Рис.1 ) складається з циліндричного корпуса 1, з одного боку якого надіта оправа патрону 2 з електричною лампою 3 та клемами 4 для підключення до джерела струму.
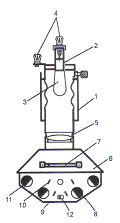
Рис. 1
Оправа з патроном обертається на корпусі, що дозволяє правильно встановити освітлювач для отримання більш чіткого відбивання променів від екрана. В корпусі нерухомо закріплено конденсор 5. з переднього боку корпус закінчується камерою 6, в яку вставляється світлофільтр 7 та коробка 8 з променевим пристроєм. Коробка вільно вставляється в пази корпусу і має всередині щиток з п`ятьма щілинами 9, чотири нерухомих дзеркала 10 і чотири дзеркала 11, які можуть повертатись з ручками для їх повертання. В передній частині коробки є поворотна заслінка 12 для прикриття середнього променя. Промені світла виходячи з конденсорної лінзи проходять крізь щілини і, відбиваються від дзеркала, дають п`ять в системі S` рівняння плоскої світлової хвилі, що поширюється від джерела до приймача:
![]()
(1)
де ![]() - частота хвилі у системі S`; с – швидкість світла, однакова в усіх системах відліку; у виразі фази взято знак плюс, оскільки хвиля поширюється у напрямі, протилежному напряму осі Ox`.
- частота хвилі у системі S`; с – швидкість світла, однакова в усіх системах відліку; у виразі фази взято знак плюс, оскільки хвиля поширюється у напрямі, протилежному напряму осі Ox`.
Згідно з принципом відносності в системі S рівняння розглядуваної хвилі матиме аналогічний формулі (1) вигляд:
![]()
, (2)
де ![]() - частота хвилі, яку фіксує приймач у системі S .
- частота хвилі, яку фіксує приймач у системі S .
Але ж від рівняння (1) можна перейти до рівняння (2), якщо за формулами перетворення Лоренца виразити координати ![]() і
і ![]() через
через ![]() і t, тоді дістанемо:
і t, тоді дістанемо:
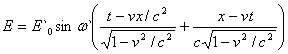
,
або в іншому вигляді
![]() , (3)
, (3)
Зіставивши рівняння (2) і (3), знаходимо:
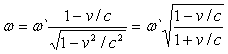 .
.
Переходячи від циклічних до звичайних частот і позначаючи частоту v` в системі джерел через v0, дістанемо формулу відображення релятивійського ефекту Доплера:
![]()
1.2 Релятивістський ефект Доплера
Нехай у системі К поширюється плоска електромагнітна хвиля, що характеризується векторами поля:
![]() ;
; ![]() (4)
(4)
При переході до системи К` вектори поля можуть змінитися, але фаза залишиться незмінною, оскільки ![]() є скаляром, тобто не залежить від системи відліку.
є скаляром, тобто не залежить від системи відліку.
Незалежність фази від системи відліку означає: якщо в системі К визначити для певних x, у, z, t фазу плоскої електромагнітної хвилі ![]() , то при переході до системи К`, за допомогою перетворень Лоренца, величина фази
, то при переході до системи К`, за допомогою перетворень Лоренца, величина фази ![]() у цій системі для відповідних x`, у`, z`, t` матимемо те саме значення.
у цій системі для відповідних x`, у`, z`, t` матимемо те саме значення.
Якщо ввести чотиривимірний вектор ![]() , то фаза може бути записана у вигляді:
, то фаза може бути записана у вигляді:
![]() =
=![]() .
.
Звідси видно, що величина ![]() є чотиривимірним вектором, бо
є чотиривимірним вектором, бо ![]() - добуток
- добуток ![]() на вектор
на вектор ![]() є скаляром як фаза хвилі, і тому може розглядатися як скалярний добуток двох чотиривимірних векторів
є скаляром як фаза хвилі, і тому може розглядатися як скалярний добуток двох чотиривимірних векторів ![]() і
і ![]() .
.
Вектор![]() називається чотиривимірним хвильовим вектором. Оскільки
називається чотиривимірним хвильовим вектором. Оскільки ![]() є чотиривимірним вектором, то при переході від однієї системи відліку до іншої він змінюється за формулами перетворень Лоренца. Запишемо формули перетворення для чотиривимірного вектора
є чотиривимірним вектором, то при переході від однієї системи відліку до іншої він змінюється за формулами перетворень Лоренца. Запишемо формули перетворення для чотиривимірного вектора ![]() :
:
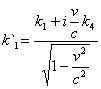 ;
; ![]() ; (5)
; (5)
![]() ;
; 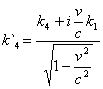 .
.
Компоненти вектора ![]() у тривимірному записі мають вигляд:
у тривимірному записі мають вигляд:
![]() ;
;
![]() .
.
Тут і далі ![]() - кути між осями Х`, Y`, Z` відповідно і хвильовим вектором k`. Рівняння (5) тепер матимуть вигляд:
- кути між осями Х`, Y`, Z` відповідно і хвильовим вектором k`. Рівняння (5) тепер матимуть вигляд:
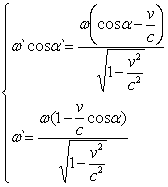
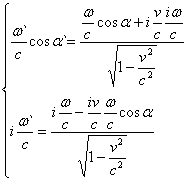 ,(6)
,(6)
Поділивши перше рівняння (6) на друге, дістанемо:
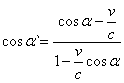 . (7)
. (7)
З другого і третього рівнянь (5) знайдемо аналогічно:
![]()
де ![]()
![]() - кути між вектором k і відповідно осями Х, Y, Z.
- кути між вектором k і відповідно осями Х, Y, Z.
З цих рівнянь,підставляючи в них ![]() з (6), знайдемо:
з (6), знайдемо:
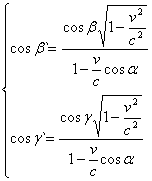 . (8)
. (8)
З рівнянь (6)-(8) видно, як змінюються напрям поширення і частота електромагнітних хвиль при переході від системи К до К`.
З рівнянь (7) і (8) випливає існування аберації світла при спостереженні зірок. Нехай зірка нерухома в системі К. Якщо промінь від неї перпендикулярний до напряму руху Землі і лежить у площині ОХУ, то
![]() ;
; ![]() ;
; ![]() .
.
Підставляючи ці значення у (7) і (8), матимемо для Землі (систем К`), рухається відносно зірки з швидкістю v:
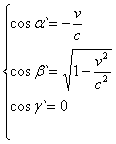
Оскільки ![]() то в системі К` промінь зірки також ледить у площині О Х`Y`. Далі матимемо:
то в системі К` промінь зірки також ледить у площині О Х`Y`. Далі матимемо:
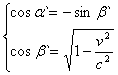
,
Звідки знайдемо:
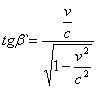 .
.
Для малих ![]() (коли
(коли ![]() <<c ) дістанемо відомий вираз:
<<c ) дістанемо відомий вираз:
![]() .
.
Тут ![]() - кут, що визначає величину аберації зірок.
- кут, що визначає величину аберації зірок.
З другої формули (5) визначимо ![]() :
:
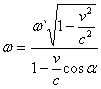 . (9)
. (9)
Отже, якщо тіло випромінює хвилі з частотою ![]() , рухається з швидкість
, рухається з швидкість ![]() , то в нерухомій системі К частота, згідно з (9), буде
, то в нерухомій системі К частота, згідно з (9), буде ![]() . Це явище буде ефектом Доплера. На відміну від класичної теорії, релятивістський ефект Доплера існує і при
. Це явище буде ефектом Доплера. На відміну від класичної теорії, релятивістський ефект Доплера існує і при ![]() (поперечний ефект Доплера).
(поперечний ефект Доплера).
Похожие работы
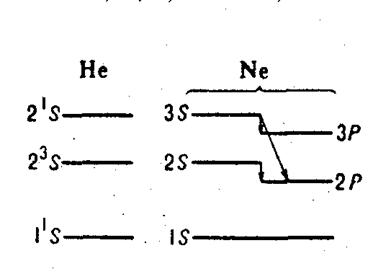
... яка була накопичена до п'ятидесятих років у радіочастотній й оптичній спектроскопії і які згодом отримали своє використання у квантовій електроніці. Розділ 2. Основні поняття квантової електроніки (фізичні основи квантової електроніки) Принцип дії лазера або мазера заснований на трьох «китах» – головних поняттях квантової електроніки, а саме на поняттях вимушеного випромінювання, інверсного ...
0 комментариев