Объяснение данных опыта с позиции современных научных теорий

1.4 Объяснение данных опыта с позиции современных научных теорий

Результаты опыта О. Штерна подтвердили справедливость предсказанного Р.Клаузиусом значения скорости движения молекул газа, послужили ярким доказательством верности полученного Д. Максвеллом закона распределения числа молекул по скоростям и явились, в конечном счете, блестящим свидетельством правильности молекулярно-кинетических представлений о строении вещества, а также статистического характера закономерностей, которым подчиняется поведение молекулярных систем.

Изобразим полученный Д. Максвеллом результат графически (рис. 5). По оси абсцисс отложим возможные различные значения скоростей молекул V и интервалов этих скоростей ΔV. По оси ординат отложим ΔN/N·ΔV.

Площадь густо заштрихованной фигуры численно равна доле ΔN/N общего числа молекул N со скоростями между V и V + ΔV. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

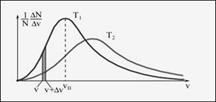
Рисунок 5 Распределение молекул по скоростям (Т2>T1) [2]

Кривые распределения молекул по скоростям имеют следующие особенности:

·  они проходят через начало координат,

·  асимптотически приближаются к оси абсцисс при бесконечно больших скоростях,

·  имеют максимум,

·  асимметричны (слева от максимума кривые идут круче, чем справа).

То, что кривая распределения проходит через начало координат, означает, что неподвижных молекул в газе нет. Из того, что кривая при бесконечно больших скоростях асимптотически приближается к оси абсцисс, следует, что слишком большие скорости молекул маловероятны. Значение наиболее вероятной скорости движения молекул соответствует максимуму кривой распределения [3, C. 34]. Вид функции распределения молекул по скорости движения, которую Д. Максвелл определил теоретическим путем, качественно совпал с профилем налета атомов серебра на латунной пластинке в опыте О.Штерна. Опыт О. Штерна (наряду с опытом Ж. Перрена) был первым прямым доказательством справедливости молекулярно-кинетической теории строения вещества. В настоящее время атомно-молекулярное учение подтверждено многочисленными опытами и является общепризнанным.

1.5 Усовершенствованные опыты Штерна

Элдридж (1927 г.) и Ламмерт (1926-1929) ввели селекторы скоростей, работающие на принципе зубчатого колеса (как в опытах Физо со светом). Идея опыта схематически изображена на рис.6. Пучок молекул из печи А коллимировался на щелях и попадал на вращающиеся зубчатые диски D1 и D2.

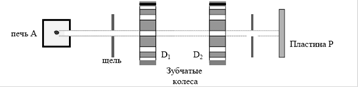
Рисунок 6 Прорези у зубчатых дисков смещены на угол a

Когда зубчатые диски покоятся (не вращаются), то атомы не проходят к регистрирующей пластинке Р (не осаждаются), поскольку щель одного диска попадает на зуб второго. Когда диски вращаются, то проходят атомы определенных скоростей, т.е. только те, которые пролетят расстояние между дисками за время их поворота на угол α.. По количеству атомов, осажденных на пластине Р, можно судить о распределении молекул по проекции скорости вдоль направления пучка. Недостатком этого метода является то, что на пластинку приходят атомы с другими скоростями, когда поворот происходит на большие углы.

Цартман попытался избежать этого эффекта и усовершенствовал опыты (рис. 7). Из печи коллимированный пучок атомов попадал на вращающийся цилиндр с отверстием. При попадании пучка в отверстие молекулы осаждались на внутренней стенке цилиндра. При этом у точки А собирались атомы или молекулы с очень большими скоростями, а к точке В – более медленные молекулы.

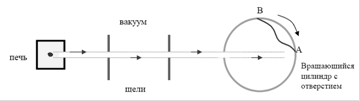
Рисунок 7

Если диаметр цилиндра равен d, то расстояние от точки А на стенку цилиндра, куда осаждаются молекулы равно:

где v – скорость молекул, а ω - угловая скорость вращения цилиндра. По почернению пластины (по числу осажденных молекул) можно судить о распределении молекул по скоростям.

Все эксперименты получили результаты в согласии с Максвелловским распределением молекул по скоростям.

2. Конструктивные особенности метода

Установка состоит из двух коаксиальных (имеющих одну ось симметрии) цилиндров между которыми создавался вакуум. Вдоль оси цилиндров натянута платиновая нить, покрытая серебром. При пропускании через нее электрического тока атомы серебра испарялись. Во внутреннем цилиндре вырезалась щель через, которую атомы серебра проникали на поверхность внешнего цилиндра, оставляя на ней след в виде узкой вертикальной полоски. При приведении цилиндров во вращение с постоянной угловой скоростью w след, оставляемый молекулами серебра смещался и размывался. Действительно, на атомы серебра в неинерциальной системе отсчета, связанной с вращающимися цилиндрами действует сила Кориолиса Fк

Fк = 2·m·[v·w]. (2.1)

Эта сила отклоняет атомы серебра от прямолинейного распространения. Средняя величина смещения атомов Ds равна:

Ds = w·R·Dt = w2·R/<v>. (2.2)

Измерив величину Ds из эксперимента, исходя из формулы (14.28), можно найти среднюю скорость движения молекул.

Ее значение совпадает с теоретическим значением, полученным с помощью формулы Максвелла.

2.1 Коаксиальные цилиндры

Коаксиальные цилиндры - два вертикальных цилиндра, имеющие параллельную общую центральную ось и различный диаметр , один из которых вращается, а второй неподвижен.

Рисунок 8