Навигация
Рассчитать прогнозные значения результата, если прогнозные значения факторов составляют 80% от их максимальных значений
7011
знаков
1
таблица
2
изображения
4. Рассчитать прогнозные значения результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
1. Рассчитаем параметры линейного уравнения множественной регрессии с полным перечнем факторов, используя инструмент «регрессия» пакета анализа. В массив «входной интервал Y» вводим диапазон ячеек, содержащих значения результата Y – B2:B27; в массив «входной интервал X» вводим диапазон ячеек, содержащих значения фактора X – C2:D27, активизируем флажки «метки», «новый рабочий лист» и «остатки», затем нажимаем клавишу «ок».
В результате получаем следующее линейное уравнение множественной регрессии:
2а. Оценим статистическую значимость параметров регрессионной модели с помощью t – критерия. Фактор xj является статистически значимым, если параметр ajпри этом факторе значим. Для проверки значимости параметра ajиспользуем столбец «t – статистка» таблицы 4 дисперсионного анализа приложения 2.
Имеем:
Сравним расчётные значения t – критерия с табличным значением tтабл.=2,064.
, значит, параметр a0 незначим.
, значит, параметр a1 значим, и фактор x1 при данном параметре является статистически значимым, его следует включить в модель.
, значит, параметр a3 значим и фактор x3
, значит, параметр a4 незначим, и фактор x4 при данном параметре не является статистически значимым, его следует исключить из модели.
, значит, параметр a4 незначим, и фактор x4 при данном параметре не является статистически значимым, его следует исключить из модели.
2б. Проверим нулевую гипотезу о значимости уравнения с помощью F – критерия (α=0,05). Для этого находим расчётное значение данного критерия с помощью функции «FРАСПОБР» мастера функций Excel: в массив «вероятность» вводим значение уровня значимости α=0,05, в массив «число степеней свободы1» вводим значение k1=m=2 (т.к. в модели 2 фактора: х 1 и х 3), в массив «число степеней свободы2» вводим значение k2=n-m-1=25-2-1=24. Затем полученное расчётное значение Fрасч.=3,403 сравниваем с табличным значением Fтабл.=80,419, которое берём из столбца «F» таблицы 4 дисперсионного анализа.
3,403<80,419, значит, уравнение регрессии незначимо.
2в. Проверим качество уравнения регрессии с помощью коэффициента детерминации по следующей формуле по данным таблицы 7(см. приложение 3):
,
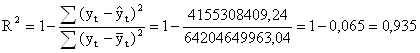значит, построенная линейная модель множественной регрессии точная, а значит, и качественная.
3а. Отобранные информативные факторы в модель по t - критерию для коэффициентов регрессии представлены в таблице 6 приложения 3. Построим модель только с информативными факторами x1 и x3, используя инструмент «регрессия» пакета анализа данных (см. приложение 5).
В результате получаем следующее линейное уравнение множественной регрессии:
.
3б. Оценим влияние значимых факторов на результат с помощью коэффициентов эластичности, β- и Δ-коэффициентов. Вычислим коэффициент эластичности для фактора х1 последующей формуле:
-
если фактор х1 увеличить на 1%, то результат y увеличится на 50%.
Аналогично находим коэффициент эластичности для фактора х3:
-
если фактор х3 увеличить на 1%, то результат y увеличится на 42%.
Находим β-коэффициенты. Для этого сначала вычислим СКО x1 и x3, используя функцию СТАНДОТКЛОН мастера функций Excel. В ячейку С32 вводим формулу:
= СТАНДОТКЛОН (С7:С31).
Аналогичную формулу вводим в ячейку D32 для нахождения СКО для фактора х3:
= СТАНДОТКЛОН(D7: D31).
Полученные значения Sxj подставим в формулы (*) и (**). В ячейку С35 вводим формулу:
=G35*C32/B32.
В ячейку D35 вводим формулу:
=H35*D32/B32.
(*)
.(**)
Получаем:
Если фактор х1 увеличить на Sx1=12994,033, то результат y изменится на
Если фактор х3 увеличить на Sx3=422015,64, то результат изменится на
Для нахождения Δ-коэффициента вычислим сначала коэффициент парной корелляции, используя инструмент «корелляция» пакета анализа данных, затем его значения подставляем в формулу:
.
В ячейку С36 вводим формулу:
=0,956*С35/0,935.
Получаем: 
, значит, 50% влияния оказывает фактор х1.
Аналогично находим Δ-коэффициент для фактора х3. В ячейку D36 вводим формулу:
=0,954*D35/0,935.
Получаем: 
, значит, 47% влияния оказывает фактор х3.
4. Найдём прогнозные значения результата y, если прогнозные значения факторов x составляют 80% от их максимальных значений.
- интервальный прогноз.
- средняя квадратическая ошибка прогноза.
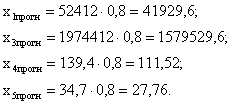
- точечный прогноз.
Похожие работы
... труда – объем произведенной продукции, средняя численность и средняя заработная плата на 1 работающего – снизились в связи с падением объемов производства и реализации продукции. 1.2 Финансовое положение предприятия ОАО "СЗТТ" Финансовое состояние является комплексным понятием, которое зависит от многих факторов и характеризуется системой показателей, отражающих наличие и размещение средств ...
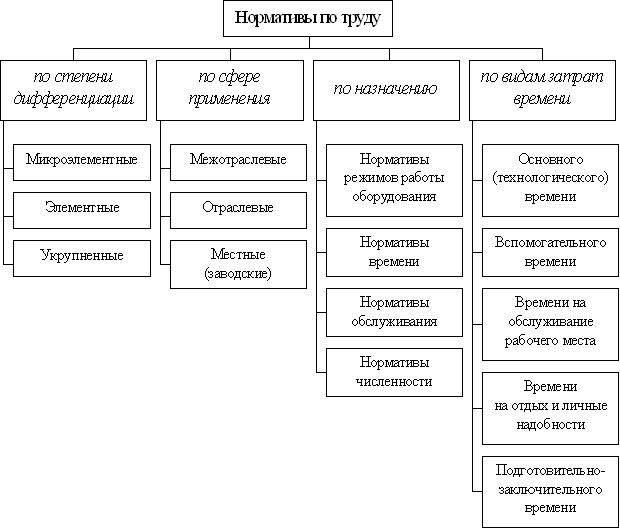
... снижает точность норм по сравнению с дифференцированными нормативами. По сфере применения нормативы подразделяются на межотраслевые, отраслевые и местные. Межотраслевые (общемашиностроительные) предназначены для нормирования труда на типичных работах, выполняемых на предприятиях различных отраслей промышленности. Наиболее характерным примером таких нормативов являются «Общемашиностроительные ...
... микроскопов, постов на их базе. 2 Анализ технико-экономических показателей предприятия Для проведения анализа технико-экономических показателей работы предприятия воспользуемся данными, приведёнными в табл. 1. Таблица 1 Показатели производственно - финансовой деятельности РУП «Завод точного машиностроения» Наименование реквизита Ед. изм. 2005 отчет 2006 оценка 2007 прогноз 1 2 ...
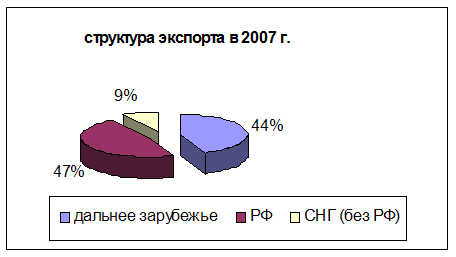
... 030 тыс. руб. 4. Сравнительный подход к оценке стоимости бизнес-линии В данном подходе для вычисления стоимости бизнес-линии используется метод рынка капитала. Особенность медота заключается в том, чтобы сориентировать итоговую величину стоимости на рыночные цены купли-продажи акций, принадлежащих сходным предприятиям. Предполагается, что рациональный инвестор действет по принципу замещения ...
0 комментариев