Навигация
Оценка параметров генеральной совокупности
2. Оценка параметров генеральной совокупности
2.1 Основные формы статистических показателей и виды их оценки
Статистические показатель – обобщающая количественная характеристика части или всей совокупности явлений в конкретных условиях места и времени. В теории несплошного наблюдения показатель выражается в следующих формах:
среднее значение признаков в совокупности;
суммарное значение признака по совокупности;
доля единиц в совокупности, обладающих определенным значением признака;
число единиц в совокупности, обладающих определенным значением признака;
отношения признаков в совокупности.
Для генеральной и выборочной совокупностей соответственно рассчитываются свои статистические показатели.
Среднее значение признака в совокупности находят по формулам:
для генеральной совокупности
 ,
,
![]()
где N - численность генеральной совокупности, xi – соответствующее значение признака;
для выборочной совокупности
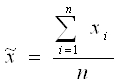 ,
,
где n – численность выборочной совокупности, xi – соответствующее значение признака;
суммарное значение признака в совокупности находят по формулам:
для генеральной совокупности
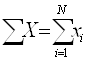 ,
,
где xi – соответствующее значение признака;
для выборочной совокупности
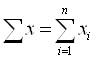 ,
,
где n – численность выборочной совокупности; xi – соответствующее значение признака;
долю единиц в совокупности, обладающих определенным значением признака находят по формулам:
для генеральной совокупности
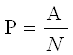 ,
,
где A - число единиц, обладающих определенным значением признака, N - численность генеральной совокупности;
для выборочной совокупности
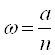 ,
,
где a - число единиц, обладающих определенным значением признака, n – численность выборочной совокупности;
число единиц, обладающих определенным значением признака, находят по формулам:
для генеральной совокупности
![]() ,
,
где P – доля единиц в совокупности, обладающих определенным значением признака, N – численность генеральной совокупности;
для выборочной совокупности
![]() ,
,
![]() - доля единиц в совокупности, обладающих определенным значением признака, n – численность выборочной совокупности;
- доля единиц в совокупности, обладающих определенным значением признака, n – численность выборочной совокупности;
отношения признаков в совокупности (отношение двух средних или суммарных значений признаков) находят по формулам:
для генеральной совокупности
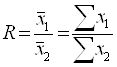 ,
,
где ![]() - среднее значение признака
- среднее значение признака ![]() в генеральной совокупности;
в генеральной совокупности;
для выборочной совокупности
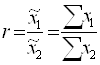 ,
,
где ![]() - среднее значение признака
- среднее значение признака ![]() в выборочной совокупности.
в выборочной совокупности.
Существует два вида оценок форм статистических показателей: простая и сложная. Сложная оценка - оценка по отношению, по регрессии, по разности, по произведению, по скорректированным весам. Сложные оценки, возможно, производить при наличии дополнительной информации о признаке в генеральной совокупности. Но в большинстве исследований подобной информации нет, поэтому чаще используется простая оценка генеральных параметров.
Оценка - приближенное значение неизвестного параметра генеральной совокупности, полученное на основании результатов выборочного наблюдения.
2.2 Точечная и интервальная оценка генеральных параметров
Оценки являются случайными величинами и бывают двух видов:
точечная - оценка параметра в генеральной совокупности одним числом;
интервальная - предполагает построение числового интервала, относительно которого с заданной вероятностью можно утверждать, что внутри него находится оцениваемый параметр генеральной совокупности. Интервальная оценка предполагает расчет нижней и верхней границы интервала. Между точечной и интервальной оценками существует взаимосвязь, которую можно представить следующим образом:
Верхняя (нижняя) граница интервала = точечная оценка ![]() ошибка доверительного интервала (ошибка репрезентативности).
ошибка доверительного интервала (ошибка репрезентативности).
Ошибка репрезентативности присуще только выборочному наблюдению и возникает в силу того, что выборочная совокупность не полностью воспроизводит генеральную совокупность. Она представляет собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборных и соответствующих генеральных показателей. Для каждого конкретного выборочного наблюдения значение ошибки репрезентативности может быть определено по соответствующим формулам, которые зависят от вида, метода и способа формирования выборочной совокупности [№7, стр. 88].
Ошибки репрезентативности бывают двух видов: предельная (![]() ) и средняя (
) и средняя (![]() ) и соответственно
) и соответственно
![]() ,
,
где t - коэффициент доверия, который зависит от уровня вероятности, с которым результаты выборки распределяются на генеральную совокупность; t определяется по таблице вероятностей Лапласа:
при значении t равном 1, вероятность равна 0,682;
при значении t равном 2, вероятность равна 0,954;
при значении t равном 3, вероятность равна 0,997;
при значении t равном 4, вероятность равна 0,999.
При типическом отборе аналитическое выравнивание точечных и интервальных оценок генеральных параметров обусловлено механизмом отбора. При типическом отборе предполагается деление генеральной совокупности на группы и эти группы должны быть однородны с точки зрения вариации значения группировочного признака. Ну а далее из типов отбор осуществляется либо собственно-случайным способом, либо механическим. Собственно-случайный применяется, когда единицы генеральной совокупности располагаются в случайном порядке. Всем единицам генеральной совокупности присваивается порядковый номер, затем осуществляется отбор единиц в выборочную совокупность следующими способами:
по жребию;
по таблице случайных чисел;
через генерацию случайных чисел в MS Excel.
Механический отбор применяется, когда единицы в генеральной совокупности упорядочены. Суть механического отбора состоит в том, что единицам генеральной совокупности присваиваются порядковый номер, затем генеральная совокупность делится на число групп равных численности и из каждой группы берется один представитель.
Рассмотрим точечную и интервальную оценку генеральных параметров при типическом отборе.
Среднее значение признака в совокупности ![]() находят по формулам:
находят по формулам:
точечная оценка
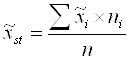 ,
,
где ![]() - выборочная стратифицированная средняя величина,
- выборочная стратифицированная средняя величина, ![]() - выборочная средняя величина в i-той страте, ni - численность выборки в i-той страте, n - численность выборки;
- выборочная средняя величина в i-той страте, ni - численность выборки в i-той страте, n - численность выборки;
интервальная оценка
![]() ,
,
где ![]() - выборочная стратифицированная средняя величина,
- выборочная стратифицированная средняя величина, ![]() - предельная ошибка выборочной стратифицированной средней величины;
- предельная ошибка выборочной стратифицированной средней величины;
суммарное значение признака в совокупности ![]() находят по формулам:
находят по формулам:
точечная оценка
![]() ,
,
где ![]() - выборочная стратифицированная средняя величина, N – численность генеральной совокупности;
- выборочная стратифицированная средняя величина, N – численность генеральной совокупности;
интервальная оценка
![]() ,
,
где ![]() - выборочная стратифицированная средняя величина,
- выборочная стратифицированная средняя величина, ![]() - предельная ошибка выборочной стратифицированной средней величины, N – численность генеральной совокупности;
- предельная ошибка выборочной стратифицированной средней величины, N – численность генеральной совокупности;
долю единиц в совокупности, обладающих определенным значением признака ![]() находят по формулам:
находят по формулам:
точечная оценка
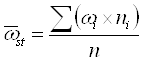 ,
,
где ![]() - выборочная стратифицированная доля,
- выборочная стратифицированная доля, ![]() - выборочная доля в i-той страте, ni - численность выборки в i-той страте, n - численность выборки;
- выборочная доля в i-той страте, ni - численность выборки в i-той страте, n - численность выборки;
интервальная оценка
![]() ,
,
где ![]() - выборочная стратифицированная доля,
- выборочная стратифицированная доля, ![]() - предельная ошибка выборочной стратифицированной доли;
- предельная ошибка выборочной стратифицированной доли;
число единиц, обладающих определенным значением признака![]() , находят по формулам:
, находят по формулам:
точечная оценка
![]() ,
,
где ![]() - выборочная стратифицированная доля, N – численность генеральной совокупности;
- выборочная стратифицированная доля, N – численность генеральной совокупности;
интервальная оценка
![]() ,
,
где ![]() - выборочная стратифицированная доля,
- выборочная стратифицированная доля, ![]() - предельная ошибка выборочной стратифицированной доли, N - численность генеральной совокупности;
- предельная ошибка выборочной стратифицированной доли, N - численность генеральной совокупности;
отношения признаков в совокупности (отношение двух средних или суммарных значений признаков) ![]() находят по формулам:
находят по формулам:
точечная оценка
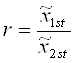 ;
;
интервальная оценка
![]() ,
,
где ![]() рассчитывается по формуле:
рассчитывается по формуле:
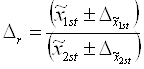 ,
,
где ![]() - предельная ошибка отношений двух средних величин.
- предельная ошибка отношений двух средних величин.
Интервальное оценивание предполагает расчет предельных, а значит и средних ошибок выборки. Расчет ошибок выборки зависит от:
1) разновидностей типического отбора:
а) непропорциональный численности отдельных типов;
б) пропорциональный численности типов;
в) пропорциональный численности отдельных типов и вариации группировочного признака;
2) метода отбора:
а) повторный;
б) бесповторный.
Рассмотрим расчет средней ошибки репрезентативности при соответствующих разновидностях типического отбора.
Среднюю ошибку выборки при повторном методе находят по формулам:
а) для отбора непропорционального численности типов:
для средней количественного признака
![]() =
= 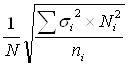 ,
,
где N – численность генеральной совокупности, ![]() - дисперсия i-той группы, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
- дисперсия i-той группы, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
для доли (альтернативного признака)
![]() =
= 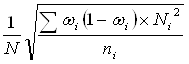 ,
,
где ![]() - выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
- выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
б) для отбора пропорционального численности типов:
для средней количественного признака
![]() =
= 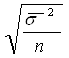 ,
,
где ![]() - средняя из групповых дисперсий, n – численность выборочной совокупности,
- средняя из групповых дисперсий, n – численность выборочной совокупности,
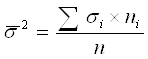 ,
,
где ![]() - среднее квадратическое отклонение в i-той группе, ni – численность выборочной совокупности в i-том типе, n – численность выборочной совокупности;
- среднее квадратическое отклонение в i-той группе, ni – численность выборочной совокупности в i-том типе, n – численность выборочной совокупности;
для доли (альтернативного признака)
![]() =
=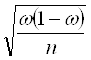 ,
,
где ![]() - доля единиц в совокупности, n – численность выборки;
- доля единиц в совокупности, n – численность выборки;
в) для отбора пропорционального численности отдельных типов и вариации группировочного признака:
для средней количественного признака
![]() =
=  ,
,
где N – численность генеральной совокупности, ![]() - среднее квадратическое отклонение в i-той группе, Ni – численность признаков в соответствующем типе, n – численность выборки;
- среднее квадратическое отклонение в i-той группе, Ni – численность признаков в соответствующем типе, n – численность выборки;
для доли (альтернативного признака)
![]() =
=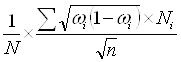 ,
,
где N – численность генеральной совокупности, ![]() - выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, n – численность выборки;
- выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, n – численность выборки;
среднюю ошибку выборки при бесповторном методе находят по формулам:
а) для отбора непропорционального численности типов:
для средней количественного признака
![]() =
=  ,
,
где N – численность генеральной совокупности, ![]() - дисперсия i-той группы, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
- дисперсия i-той группы, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
для доли (альтернативного признака)
![]() =
= 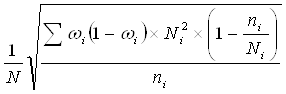 ,
,
где N – численность генеральной совокупности, ![]() - выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
- выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, ni – численность выборочной совокупности в i-том типе;
б) для отбора пропорционального численности типов:
для средней количественного признака
![]() =
= 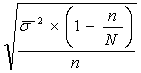 ,
,
где ![]() - средняя из групповых дисперсий, n – численность выборки, N – численность генеральной совокупности;
- средняя из групповых дисперсий, n – численность выборки, N – численность генеральной совокупности;
для доли (альтернативного признака)
![]() =
= 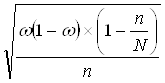 ,
,
где ![]() - доля единиц в совокупности, n – численность выборки, N – численность генеральной совокупности;
- доля единиц в совокупности, n – численность выборки, N – численность генеральной совокупности;
в) для отбора пропорционального численности отдельных типов и вариации группировочного признака:
для средней количественного признака
![]() =
= 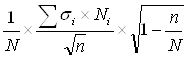 ,
,
где N - численность генеральной совокупности, ![]() - среднее квадратическое отклонение в i-той группе, Ni – численность признаков в соответствующем типе, n – численность выборки, N – численность генеральной совокупности;
- среднее квадратическое отклонение в i-той группе, Ni – численность признаков в соответствующем типе, n – численность выборки, N – численность генеральной совокупности;
для доли (альтернативного признака)
![]() =
=  ,
,
где N - численность генеральной совокупности, ![]() - выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, n – численность выборки, N – численность генеральной совокупности.
- выборочная доля в i-той страте, Ni – численность признаков в соответствующем типе, n – численность выборки, N – численность генеральной совокупности.
Похожие работы
... равна Средняя ошибка выборки для доли (альтернативного признака) при серийном отборе: (повторный отбор) (бесповторный отбор)[3] Производственные и финансовые показатели Статистика финансов предприятий на основе присущих ей статистических методов изучает количественные характеристики денежных отношений, связанных с образованием, распределением и использованием финансовых ресурсов ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... вносится поправка в общую численность скота, находящегося у населения данного поселка. Способы отбора единиц из генеральной совокупности. В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения. Основным условием проведения выборочного обследования является предупреждение возникновения ...

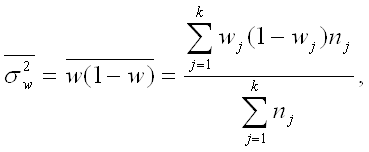
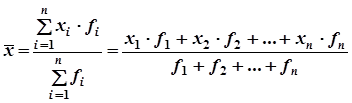
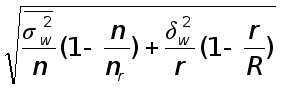
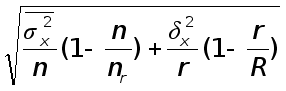
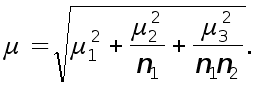
0 комментариев