Навигация
3. Расчетная часть
По данным таблицы 1 «Выручка от реализации товаров и услуг предприятиями обрабатывающей промышленности» необходимо организовать выборочное наблюдение предприятий.
Таблица 1 «Выручка от реализации товаров и услуг предприятиями обрабатывающей промышленности»
| № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. |
| 1 | 6,3 | 31 | 12,4 | 61 | 7,0 | 91 | 15,4 | 121 | 20,3 |
| 2 | 3,6 | 32 | 10,0 | 62 | 5,8 | 92 | 17,1 | 122 | 18,1 |
| 3 | 3,7 | 33 | 4,3 | 63 | 7,3 | 93 | 14,6 | 123 | 8,3 |
| 4 | 2,1 | 34 | 5,4 | 64 | 4,4 | 94 | 6,5 | 124 | 1,6 |
| 5 | 10,2 | 35 | 17,4 | 65 | 5,9 | 95 | 13,9 | 125 | 1,1 |
| 6 | 8,2 | 36 | 3,7 | 66 | 7,0 | 96 | 7,6 | 126 | 8,5 |
| 7 | 22,6 | 37 | 8,8 | 67 | 3,2 | 97 | 12,4 | 127 | 9,0 |
| 8 | 12,6 | 38 | 4,0 | 68 | 3,8 | 98 | 16,0 | 128 | 8,9 |
| 9 | 5,2 | 39 | 20,0 | 69 | 4,4 | 99 | 5,8 | 129 | 6,0 |
| 10 | 5,1 | 40 | 5,3 | 70 | 7,0 | 100 | 17,0 | 130 | 5,3 |
| 11 | 5,8 | 41 | 4,0 | 71 | 3,8 | 101 | 1,1 | 131 | 5,4 |
| 12 | 22,0 | 42 | 7,9 | 72 | 1,0 | 102 | 4,5 | 132 | 7,1 |
| 13 | 10,0 | 43 | 18,4 | 73 | 1,7 | 103 | 10,5 | 133 | 4,3 |
| 14 | 16,5 | 44 | 10,6 | 74 | 3,2 | 104 | 2,9 | 134 | 4,6 |
| 15 | 13,5 | 45 | 5,0 | 75 | 3,0 | 105 | 5,3 | 135 | 8,0 |
| 16 | 10,0 | 46 | 6,6 | 76 | 6,7 | 106 | 11,5 | 136 | 7,9 |
| 17 | 25,3 | 47 | 3,5 | 77 | 5,2 | 107 | 2,6 | 137 | 17,5 |
| 18 | 15,0 | 48 | 7,3 | 78 | 5,3 | 108 | 12,5 | 138 | 17,7 |
| 19 | 11,6 | 49 | 6,7 | 79 | 1,1 | 109 | 2,7 | 139 | 21,6 |
| 20 | 8,2 | 50 | 17,0 | 80 | 1,5 | 110 | 1,0 | 140 | 22,9 |
| 21 | 6,1 | 51 | 3,8 | 81 | 8,3 | 111 | 3,3 | 141 | 7,2 |
| 22 | 4,0 | 52 | 4,0 | 82 | 9,0 | 112 | 13,7 | 142 | 25,0 |
| 23 | 5,0 | 53 | 6,1 | 83 | 15,0 | 113 | 14,0 | 143 | 21,0 |
| 24 | 14,7 | 54 | 9,3 | 84 | 10,7 | 114 | 7,9 | 144 | 24,1 |
| 25 | 6,7 | 55 | 9,8 | 85 | 9,0 | 115 | 14,6 | 145 | 19,4 |
| 26 | 7,7 | 56 | 5,5 | 86 | 1,3 | 116 | 15,0 | 146 | 7,7 |
| 27 | 9,7 | 57 | 4,6 | 87 | 16,1 | 117 | 1,4 | 147 | 20,1 |
| 28 | 20,2 | 58 | 4,5 | 88 | 9,3 | 118 | 1,3 | 148 | 24,9 |
| 29 | 3,8 | 59 | 17,4 | 89 | 11,8 | 119 | 6,1 | 149 | 23,7 |
| 30 | 20,5 | 60 | 5,7 | 90 | 1,1 | 120 | 17,0 | 150 | 25,2 |
1) Во-первых, чтобы начать организовывать выборочное наблюдение, необходимо проверить данную совокупность на однородность. Для этого рассчитывается коэффициент вариации по формуле:
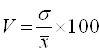 ,
,
где ![]() - среднее квадратическое отклонение генеральной совокупности,
- среднее квадратическое отклонение генеральной совокупности, ![]() - среднее значение признака
- среднее значение признака ![]() в генеральной совокупности.
в генеральной совокупности.
Для расчета коэффициента вариации необходимо сначала рассчитать среднее квадратическое отклонение по формуле:
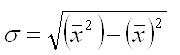 ,
,
где
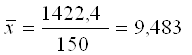 ,
,
![]() ,
,
тогда коэффициент вариации равен:
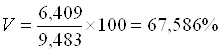 .
.
Коэффициент вариации 67,586%>33%, следовательно, совокупность неоднородна и тогда необходимо эту совокупность разбить на три группы с равным интервалом.
2) Находим интервал по формуле:
 ,
,
тогда
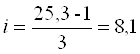 .
.
Делим данную совокупность на три группы с интервалом i=8,1 – получаем:
а) первая группа с границами 1,0-9,1, где Ni = 91:
Таблица 2 «1-ая группа 1,0-9,1»
| № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. |
| 1 | 6,3 | 53 | 6,1 | 94 | 6,5 |
| 2 | 3,6 | 56 | 5,5 | 96 | 7,6 |
| 3 | 3,7 | 57 | 4,6 | 99 | 5,8 |
| 4 | 2,1 | 58 | 4,5 | 101 | 1,1 |
| 6 | 8,2 | 60 | 5,7 | 102 | 4,5 |
| 9 | 5,2 | 61 | 7 | 104 | 2,9 |
| 10 | 5,1 | 62 | 5,8 | 105 | 5,3 |
| 11 | 5,8 | 63 | 7,3 | 107 | 2,6 |
| 20 | 8,2 | 64 | 4,4 | 109 | 2,7 |
| 21 | 6,1 | 65 | 5,9 | 110 | 1 |
| 22 | 4 | 66 | 7 | 111 | 3,3 |
| 23 | 5 | 67 | 3,2 | 114 | 7,9 |
| 25 | 6,7 | 68 | 3,8 | 117 | 1,4 |
| 26 | 7,7 | 69 | 4,4 | 118 | 1,3 |
| 29 | 3,8 | 70 | 7 | 119 | 6,1 |
| 33 | 4,3 | 71 | 3,8 | 123 | 8,3 |
| 34 | 5,4 | 72 | 1 | 124 | 1,6 |
| 36 | 3,7 | 73 | 1,7 | 125 | 1,1 |
| 37 | 8,8 | 74 | 3,2 | 126 | 8,5 |
| 38 | 4 | 75 | 3 | 127 | 9 |
| 40 | 5,3 | 76 | 6,7 | 128 | 8,9 |
| 41 | 4 | 77 | 5,2 | 129 | 6 |
| 42 | 7,9 | 78 | 5,3 | 130 | 5,3 |
| 45 | 5 | 79 | 1,1 | 131 | 5,4 |
| 46 | 6,6 | 80 | 1,5 | 132 | 7,1 |
| 47 | 3,5 | 81 | 8,3 | 133 | 4,3 |
| 48 | 7,3 | 82 | 9 | 134 | 4,6 |
| 49 | 6,7 | 85 | 9 | 135 | 8 |
| 51 | 3,8 | 86 | 1,3 | 136 | 7,9 |
| 52 | 4 | 90 | 1,1 | 141 | 7,2 |
| 146 | 7,7 |
Рассчитываем среднее квадратическое отклонение по этой группе:
![]() ;
;
б) вторая группа с границами 9,1-17,2, где Ni = 36:
Таблица 3 «2-ая группа 9,1-17,2»
| № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. |
| 5 | 10,2 | 87 | 16,1 |
| 8 | 12,6 | 88 | 9,3 |
| 13 | 10 | 89 | 11,8 |
| 14 | 16,5 | 91 | 15,4 |
| 15 | 13,5 | 92 | 17,1 |
| 16 | 10 | 93 | 14,6 |
| 18 | 15 | 95 | 13,9 |
| 19 | 11,6 | 97 | 12,4 |
| 24 | 14,7 | 98 | 16 |
| 27 | 9,7 | 100 | 17 |
| 31 | 12,4 | 103 | 10,5 |
| 32 | 10 | 106 | 11,5 |
| 44 | 10,6 | 108 | 12,5 |
| 50 | 17 | 112 | 13,7 |
| 54 | 9,3 | 113 | 14 |
| 55 | 9,8 | 115 | 14,6 |
| 83 | 15 | 116 | 15 |
| 84 | 10,7 | 120 | 17 |
Рассчитываем среднее квадратическое отклонение по этой группе:
![]() ;
;
в) третья группа с границами 17,2-25,3, где Ni = 23:
Таблица 4 «3-я группа 17,2-25,3»
| № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. |
| 7 | 22,6 | 137 | 17,5 |
| 12 | 22 | 138 | 17,7 |
| 17 | 25,3 | 139 | 21,6 |
| 28 | 20,2 | 140 | 22,9 |
| 30 | 20,5 | 142 | 25 |
| 35 | 17,4 | 143 | 21 |
| 39 | 20 | 144 | 24,1 |
| 43 | 18,4 | 145 | 19,4 |
| 59 | 17,4 | 147 | 20,1 |
| 121 | 20,3 | 148 | 24,9 |
| 122 | 18,1 | 149 | 23,7 |
| 150 | 25,2 |
Рассчитываем среднее квадратическое отклонение по этой группе:
![]() .
.
3) Необходимо организовать 40%-ную типическую выборку:
![]() ,
,
где n – численность выборочной совокупности.
Значит, далее рассчитываем выборочную совокупность для данных полученных групп по формуле типического отбора выборочной совокупности пропорционального численности групп и вариации группировочного признака:
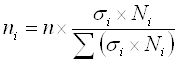 ,
,
где ![]() - среднее квадратическое отклонение соответствующей полученной группы, Ni - численность генеральной совокупности соответствующей полученной группы. Тогда
- среднее квадратическое отклонение соответствующей полученной группы, Ni - численность генеральной совокупности соответствующей полученной группы. Тогда
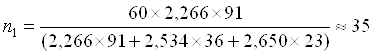 ,
,
![]() ,
,
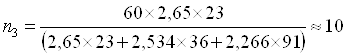 .
.
Следовательно,
n = n1+n2+n3,
60=35+15+10.
Но, проведя механическую выборку внутри образованных групп, получаем несколько другие результаты.
Проводим механическую выборку внутри первой полученной группы, границы которой 1-9,1 где ni = 46:
Таблица 5 «механический отбор 1-ой группы 1,0-9,1»
| № п/п | Выручка от реализации, млн. руб. | № п/п | Выручка от реализации, млн. руб. | |
| 1 | 6,3 | 70 | 7 | |
| 3 | 3,7 | 72 | 1 | |
| 6 | 8,2 | 74 | 3,2 | |
| 10 | 5,1 | 76 | 6,7 | |
| 20 | 8,2 | 78 | 5,3 | |
| 22 | 4 | 80 | 1,5 | |
| 25 | 6,7 | 82 | 9 | |
| 29 | 3,8 | 86 | 1,3 | |
| 34 | 5,4 | 94 | 6,5 | |
| 37 | 8,8 | 99 | 5,8 | |
| 40 | 5,3 | 102 | 4,5 | |
| 42 | 7,9 | 105 | 5,3 | |
| 46 | 6,6 | 109 | 2,7 | |
| 48 | 7,3 | 111 | 3,3 | |
| 51 | 3,8 | 117 | 1,4 | |
| 53 | 6,1 | 119 | 6,1 | |
| 57 | 4,6 | 124 | 1,6 | |
| 60 | 5,7 | 126 | 8,5 | |
| 62 | 5,8 | 128 | 8,9 | |
| 64 | 4,4 | 130 | 5,3 | |
| 66 | 7 | 132 | 7,1 | |
| 68 | 3,8 | 134 | 4,6 | |
| 136 | 7,9 | |||
| 146 | 7,7 | |||
Проводим механическую выборку внутри второй полученной группы, границы которой 9,1-17,2, где ni = 18:
Таблица 6 «Механический отбор 2-ой группы 9,1-17,2»
| № п/п | Выручка от реализации, млн. руб. |
| 5 | 10,2 |
| 13 | 10 |
| 15 | 13,5 |
| 18 | 15 |
| 24 | 14,7 |
| 31 | 12,4 |
| 44 | 10,6 |
| 54 | 9,3 |
| 83 | 15 |
| 87 | 16,1 |
| 89 | 11,8 |
| 92 | 17,1 |
| 95 | 13,9 |
| 98 | 16 |
| 103 | 10,5 |
| 108 | 12,5 |
| 113 | 14 |
| 116 | 15 |
Проводим механическую выборку внутри третьей полученной группы, границы которой 17,2-25,3, где ni = 12:
Таблица 7 «механический отбор 3-ей группы 17,2-25,3»
| № п/п | Выручка от реализации, млн. руб. |
| 7 | 22,6 |
| 17 | 25,3 |
| 30 | 20,5 |
| 39 | 20 |
| 59 | 17,4 |
| 122 | 18,1 |
| 138 | 17,7 |
| 140 | 22,9 |
| 143 | 21 |
| 145 | 19,4 |
| 148 | 24,9 |
| 150 | 25,2 |
После проведения механической выборки внутри образованных групп получаем, что:
n = 46+18+12=76.
4) Далее необходимо определить с вероятностью 0,683 границы, в которых будет находиться генеральная средняя выручка от реализации товаров и услуг.
Необходимо изначально определить среднюю ошибку репрезентативности ![]() по формуле:
по формуле:
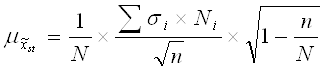 ,
,
где N – численность генеральной совокупности, ![]() - среднее квадратическое отклонение соответствующей выборочной совокупности данной группы, Ni - численность генеральной совокупности соответствующей группы, n – численность выборочной совокупности.
- среднее квадратическое отклонение соответствующей выборочной совокупности данной группы, Ni - численность генеральной совокупности соответствующей группы, n – численность выборочной совокупности.
Но прежде чем найти среднюю ошибку репрезентативности, необходимо найти среднее квадратическое отклонение выборочной совокупности каждой группы ![]() .
.
Для первой группы:
![]() ,
,
для второй группы:
![]() ,
,
для третьей группы:
![]() .
.
Далее рассчитываем ошибку репрезентативности:
 ,
,
так как вероятность P = 0,683, следовательно, t – коэффициент доверия равен 1, тогда
![]() .
.
Границы определяются как:
![]() .
.
Рассчитываем выборочную стратифицированную среднюю величину по формуле:
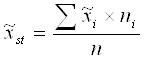 ,
,
где ![]() - выборочная средняя соответствующей группы, ni – численность выборочной совокупности соответствующей группы; тогда
- выборочная средняя соответствующей группы, ni – численность выборочной совокупности соответствующей группы; тогда
![]() .
.
Известно, что генеральная средняя равна ![]() .
.
Значит, далее определяем границы, в которых будет находиться генеральная средняя выручка от реализации товаров и услуг:
9,780-0,184<![]() <9,780+0,184,
<9,780+0,184,
9,596<![]() <9,965.
<9,965.
5) Генеральная средняя ![]() в полученные границы не входит. Следовательно, можно сделать вывод о том, что при вероятности P = 0,683 результаты выборки нельзя распространить на генеральную совокупность - выборка является непредставительной.
в полученные границы не входит. Следовательно, можно сделать вывод о том, что при вероятности P = 0,683 результаты выборки нельзя распространить на генеральную совокупность - выборка является непредставительной.
Заключение
Выборочное наблюдение используется еще с XVII века, ведь существует ряд преимуществ его перед сплошным наблюдением: во-первых, например обследуемая совокупность очень велика, практически безгранична (совокупность участков морского дна или совокупность колосьев пшеницы на поле) и тогда абсолютно невозможно применение сплошного наблюдения; во-вторых, выборочный метод позволяет сберегать значительные количества труда и средств, как на этапе сбора сведений, так и на этапе их обработки и анализа - экономия же труда и средств, получаемая при замене сплошного наблюдения выборочным имеет немаловажное значение.
На практике разработан способ отбора выборочной совокупности, который позволяет с большей вероятностью распространить результаты выборки на всю генеральную совокупность. Он получил название типической выборки.
Типический (расслоенный) отбор применяется для отбора единиц из неоднородной совокупности, который используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели.
Вообще, расслоение представляет собой полезное средство планирования отбора. Этот метод позволяет использовать априорную информацию об общей совокупности и ее совокупностях по признаку без риска потерь. Выигрыш обычно умеренный, но в некоторых случаях может быть весьма большим. Расходы по осуществлению расслоенного отбора, как правила, довольно низкие.
Типический отбор выборочной совокупности является наиболее представительным по сравнению с другими способами отбора выборочной совокупности. Но как при любом другом способе отбора выборки все же существуют некоторые неточности статистических показателей при отборе выборки в процессе несплошного наблюдения. По точности статистического показателя исследователь может судить о результатах выборочного наблюдения – можно ли распространить результаты выборочной совокупности на генеральную совокупность или нет, следовательно, проверка выборочной совокупности на точность это необходимая часть анализа при несплошном наблюдении.
Существуют два вида оценок статистических показателей на точность: точечная и интервальная. Точечная представляет собой оценку параметра в генеральной совокупности одним числом, а интервальная предполагает построение числового интервала. Интервальное оценивание предполагает расчет ошибки репрезентативности – ошибки доверительного интервала.
Ошибка репрезентативности присуще только выборочному наблюдению и возникает в силу того, что выборочная совокупность не полностью воспроизводит генеральную совокупность.
Вообще, точность статистических показателей играет огромную роль в выборочном наблюдении; точность статистических показателей показывает степень их соответствия отображаемой ими действительности. Тутубалин В.Н. справедливо пишет, что «при аккуратной статистической обработке интересуются не только результатом, но и точностью, с которой этот результат получен, а для оценки точности уже нужна статистическая модель и вообще наука» [№12, стр. 28].
Для проверки насколько представительна выборка, образованная типическим способом, в расчетной части курсовой работы произведен отбор выборочной совокупности с помощью типического отбора. По данным таблицы 1 «Выручка от реализации товаров и услуг предприятиями обрабатывающей промышленности» проверяем, однородна данная совокупность или нет. Рассчитывая коэффициент вариации, убеждаемся, что совокупность неоднородна. Тогда разбиваем ее на три группы с равными интервалами. Далее осуществляем 40%-ную типическую выборку, пропорциональную численности предприятий в отдельных группах и вариации признака, с механическим отбором внутри образованных групп. Затем определяем с вероятностью 0,683 границы, в которых будет находиться генеральная средняя выручка от реализации товаров и услуг. Но с данной вероятностью генеральная средняя выручка от реализации товаров и услуг не будет входить в полученные границы. Следовательно, можно сделать вывод, о том, что результаты выборочной совокупности нельзя распространить на генеральную совокупность, т.е. выборка непредставительна. Но если увеличить вероятность, например до 0,954, то тогда в полученные границы обязательно войдет генеральная средняя выручка от реализации товаров и услуг и, следовательно, выборка будет являться представительной.
Список использованной литературы
1. Венецкий И.Г. Теоретические и практические основы выборочного метода: Учебное пособие. – М.: Изд-во МЭСИ, 1975.
2. Джессен Р. Дж. Методы статистических обследований/Перевод с англ., под ред. и с предисловие Е.М. Четыркина. – М.: Финансы и статистика, 1985.
3. Дружинин Н.К. Выборочное наблюдение и эксперимент: (Общие логич. принципы организации). – М.: Статистика, 1977.
4. Кокрен У. Методы выборочного исследования/Пер. с англ. – М.: Статистика, 1976.
5. Методологические положения по статистике. Выпуск 3/Госкомстат России. – М, 2000.
6. Моргенштерн О. О точности экономико-статистических наблюдений. М.: Статистика, 1968.
7. Общая теория статистики: учеб. для вузов по направлению и спец. «Статистика» / И.И. Елисеева, М.М. Юзбашев; под ред. И.И. Елисеевой. – 5-е изд., перераб. доп. – М.: Финансы и статистика, 2005.
8. Практикум по теории статистики: Учеб. пособие для экон. спец. вузов [Р.А. Шмойлова, А.Б. Гусынин, В.Г. Минашкин, Н.А. Садовникова]; Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2001.
9. Статистика: Учеб. пособие / [Л.П. Харченко, В.Г. Долженкова, В.Г. Ионин и др.]; НГАЭиУ. - 2-е изд., перераб. и доп. - М.: ИНФРА-М, 2002.
10. Статистика: учебно-метод. комплекс для всех экон. спец. [В.В. Глинский и др.]; НГУЭУ, каф. статистики. – Новосибирск, 2005.
11. Суслов И.П. Основы теории достоверности статистических показателей. Новосибирск: Наука, СО, 1979.
12. Тутубалин В.Н. Статистическая обработка рядов наблюдения. М.: Знание, 1973.
13. Шварц Г. Выборочный метод. Руководство по применению статистических методов оценивания/Пер. с нем. – М.: Статистика, 1978.
Похожие работы
... равна Средняя ошибка выборки для доли (альтернативного признака) при серийном отборе: (повторный отбор) (бесповторный отбор)[3] Производственные и финансовые показатели Статистика финансов предприятий на основе присущих ей статистических методов изучает количественные характеристики денежных отношений, связанных с образованием, распределением и использованием финансовых ресурсов ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... вносится поправка в общую численность скота, находящегося у населения данного поселка. Способы отбора единиц из генеральной совокупности. В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения. Основным условием проведения выборочного обследования является предупреждение возникновения ...

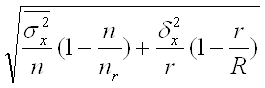
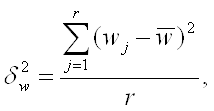
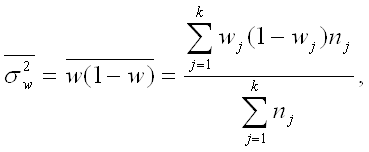
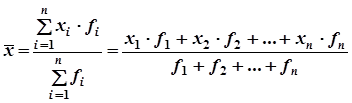
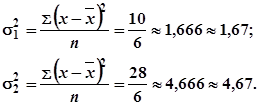
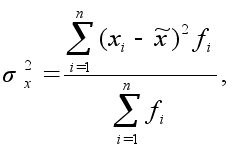
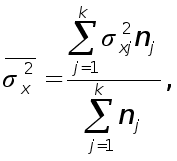
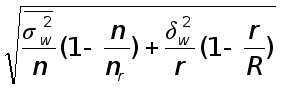
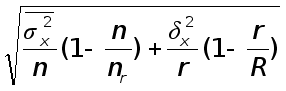
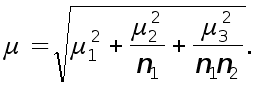
0 комментариев