Навигация
2. ПРАКТИЧНА ЧАСТИНА
Динамічне рівняння пов’язує вихідну величину ![]() засобу вимірювання із вхідною
засобу вимірювання із вхідною ![]() в динамічному режимі роботи. При його складанні в праву частину рівняння записують вхідний сигнал (причину, що привела засіб вимірювання в дію), а в ліву – вихідний сигнал (реакцію засобу вимірювання). В загальному вигляді диференціальне рівняння має вигляд:
в динамічному режимі роботи. При його складанні в праву частину рівняння записують вхідний сигнал (причину, що привела засіб вимірювання в дію), а в ліву – вихідний сигнал (реакцію засобу вимірювання). В загальному вигляді диференціальне рівняння має вигляд:
![]() (2.1)
(2.1)
В операторній формі
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
Диференціальне рівняння динамічної системи є вичерпною її характеристикою, але його коефіцієнти важко піддаються експериментальному визначенню. Тому як характеристики перетворення в часовій області використовуються імпульсна перехідна (вагова) ![]() та перехідна
та перехідна ![]() функції.
функції.
Імпульсна функція ![]() є відгуком (реакцією) динамічної системи на вхідне збурення у вигляді
є відгуком (реакцією) динамічної системи на вхідне збурення у вигляді ![]() -функції, яка за визначенням має властивості
-функції, яка за визначенням має властивості
 (2.4)
(2.4)
![]() (2.5)
(2.5)
Перехідна функція
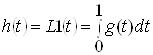 . (2.6)
. (2.6)
є відгуком динамічної системи на вхідну дію у вигляді одиничної функції ![]() , похідна якої
, похідна якої
![]() (2.7)
(2.7)
З характеристиками перетворення у часовій області однозначно пов’язані характеристики перетворення в частотній області, що є наслідком дуальності часу і частоти.
Усталена реакція на синусоїдний вхідний сигнал у загальному випадку є складною функцією параметрів засобу вимірювальної техніки і описується відповідними амплітудно-частотною та фазочастотною характеристиками, які можуть бути одержані з диференціального рівняння в результаті нижчеподаних математичних дій.
Застосувавши до диференціального рівняння при початкових нульових умовах перетворення Лапласа, одержимо передаточну функцію
 (2.8)
(2.8)
де ![]() - оператор Лапласа,
- оператор Лапласа, ![]() та
та ![]() - зображення за Лапласом відповідно вихідної та вхідної величин.
- зображення за Лапласом відповідно вихідної та вхідної величин.
Заміна оператора Лапласа в передаточній функції на ![]() дає комплексну частотну характеристику
дає комплексну частотну характеристику
 (2.9)
(2.9)
Комплексна частотна характеристика є вихідною для визначення амплітудно-частотної
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
Згідно індивідуального завдання необхідно знайти розв’язок диференціального рівняння другого порядку
![]() , (2.12)
, (2.12)
![]() . (2.13)
. (2.13)
Підставимо (2.13) в (2.12) і отримаємо:
![]() . (2.14)
. (2.14)
Розв’язком даного рівняння буде функція
![]()
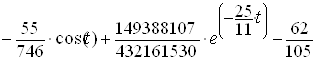 , (2.15)
, (2.15)
графічне зображення якої подано на рисунку 2.1.
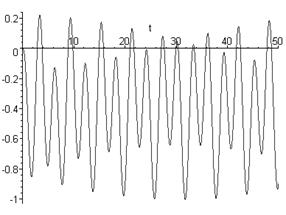
Рисунок 2.1 – Графічне представлення розв’язку диференціального рівняння
Для знаходження перехідної характеристики підставимо в (2.12) як вхідний сигнал ![]() :
:
![]()
![]() . (2.16)
. (2.16)
Отримаємо розв’язок:
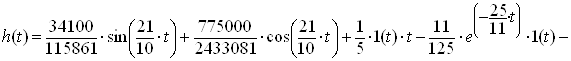
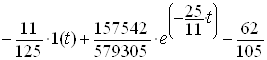 . (2.17)
. (2.17)
Графічно перехідна характеристика зображена на рисунку 2.2.
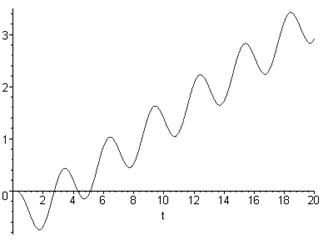
Рисунок 2.2 – Перехідна характеристика
Для знаходження імпульсної характеристики підставимо в (2.12) як вхідний сигнал ![]() :
:
![]() . (2.18)
. (2.18)
Отримаємо розв’язок:
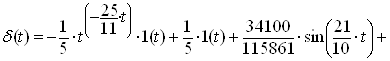
 (2.19)
(2.19)
Графічно імпульсна характеристика зображена на рисунку 2.3.
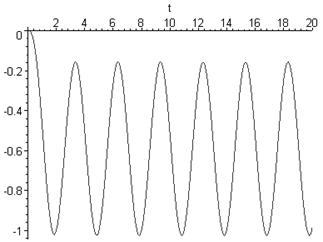
Рисунок 2.3 – Імпульсна характеристика
Знайдемо передатну функцію заданого диференціального рівняння
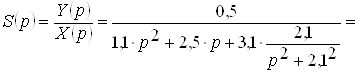
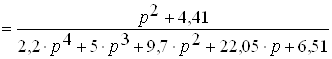 . (2.20)
. (2.20)
Замінимо оператор Лапласа в передатній функції на ![]() та отримаємо комплексну частотну характеристику
та отримаємо комплексну частотну характеристику
 . (2.21)
. (2.21)
Виділимо дійсну та уявну частини в знаменнику:
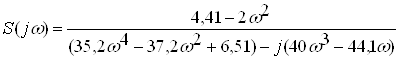 . (2.22)
. (2.22)
Помножимо чисельник та знаменник дробу на вираз, комплексно спряжений до знаменника, для того, щоб позбутись ірраціональності в знаменнику. В результаті отримаємо
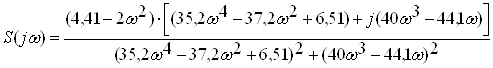 . (2.23)
. (2.23)
З даного виразу маємо дійсну
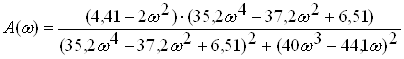 (2.24)
(2.24)
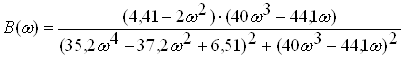 . (2.25)
. (2.25)
частини комплексної частотної характеристики.
Знайдемо амплітудно-частотну характеристику як корінь із суми піднесених до квадрату дійсної та уявної частин комплексної частотної характеристики:
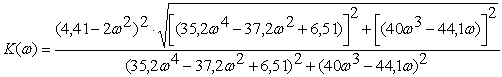 . (2.26)
. (2.26)
Замінимо ![]() , тоді
, тоді
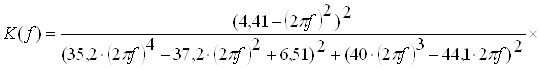
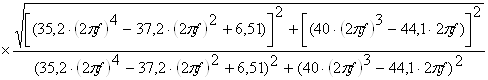 (2.27)
(2.27)
Графічно амплітудно-частотну характеристику наведено на рисунку 2.4.
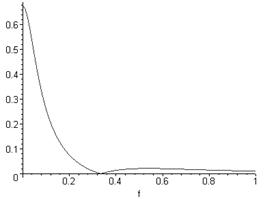
Рисунок 2.4 – Амплітудно-частотна характеристика
Знайдемо фазочастотну характеристику як мінус арктангенс відношення уявної частини комплексної частотної характеристики до дійсної
 . (2.28)
. (2.28)
Після заміни ![]() отримаємо
отримаємо
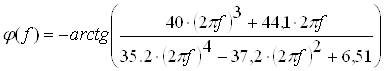 . (2.29)
. (2.29)
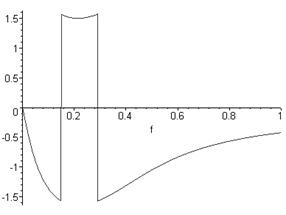
Графік фазочастотної характеристики наведено на рисунку 2.5.
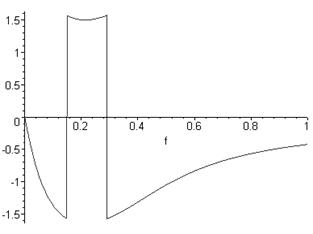
Рисунок 2.5 – Фазочастотна характеристика
Отже, в даному розділі було знайдено розв’язок диференціального рівняння другого порядку, отримано перехідну, імпульсну, амплітудно-частотну та фазочастотну характеристики. Всі розв’язки отримані за допомогою пакету прикладних програм Maple 7 і наведені в додатку А.
ВИСНОВКИ
В даній курсовій розглянуто питання визначення динамічних похибок вимірювання за допомогою динамічних характеристик засобу вимірювання.
В першому розділі розглянуто характеристики точності та правильності вимірювань, дано інтерпретацію понять роздільної здатності та класу точності засобу вимірювання, наведено методики визначення класу точності для різних типів засобів вимірювання.
В другому розділі було знайдено розв’язок диференціального рівняння другого порядку, що описує залежність вихідного сигналу засобу вимірювання від вхідного, отримано перехідну, імпульсну, амплітудно-частотну та фазочастотну характеристики, оскільки саме вони як повні динамічні характеристики дозволяють визначити динамічну похибку засобу вимірювання.
Всі розв’язки отримані за допомогою пакету прикладних програм Maple 7 і наведені в додатку А.
ПЕРЕЛІК ПОСИЛАНЬ
1. Поліщук Є.С., Дорожовець М.М., Яцук В.О., та ін. Метрологія та вимірювальна техніка: Підручник / Є.С.Поліщук, М.М.Дорожовець, В.О.Яцук, В.М.Ванько, Т.Г.Бойко; За ред. проф. Є.С.Поліщука. – Львів: Видавництво “Бескид Біт”, 2003.
2. ДСТУ 2681-94. Метрологія. Терміни та визначення. – К.: Держстандарт України, 1994.
3. Володарський Є.Т., Кухарчук В.В, Поджаренко В.О., Сердюк Г.Б. Метрологічне забезпечення вимірювань і контролю. Навчальний посібник. – Вінниця ВДТУ, 2001.
4. Кухарчук В.В., Кучерук В.Ю., Долгополов В.П., Грумінська Л.В. Метрологія та вимірювальна техніка. Навчальний посібник. – Вінниця: УНІВЕРСУМ-Вінниця, 2004.
Додаток А
Розв’язок диференційного рівняння в пакеті Maple 7
x(t):=cos(t); ode1:=1.1*diff(diff(y(t),t),t)+2.5*diff(y(t),t)+3.1*sin(2.1*t)=
=0.5*x(t);
![]()
![]()
dsolve({ode1,y(0)=0,D(y)(0)=0});

y1(t) := 34100/115861*sin(21/10*t)+775000/2433081*cos(21/10*t)-
-55/746*sin(t)-125/746*cos(t)+103507151/432161530*exp(-25/11*t)-
-41/105;

with(plots):plot({cos(t),y1(t)},t=0..50);
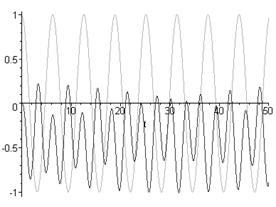
dsolve({1.1*diff(diff(y(t),t),t)+2.5*diff(y(t),t)+
+3.1*sin(2.1*t)=0.5*Heaviside(t),y(0)=0, D(y)(0)=0});
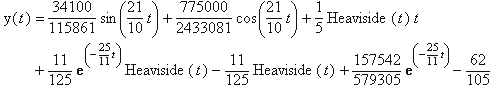
y2(t) := 34100/115861*sin(21/10*t)+775000/2433081*cos(21/10*t)+
+1/5*Heaviside(t)*t+11/125*exp(-25/11*t)*Heaviside(t)-
-11/125*Heaviside(t)+157542/579305*exp(-25/11*t)-62/105;
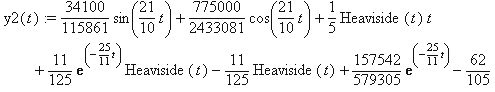
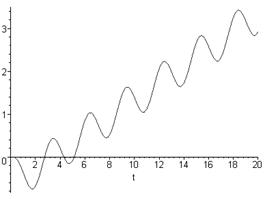
plot({y2(t)},t=0..20);
dsolve({1.1*diff(diff(y(t),t),t)+2.5*diff(y(t),t)+
+3.1*sin(2.1*t)=0.5*Dirac(t),y(0)=0, D(y)(0)=0});

y3(t) := -1/5*exp(-25/11*t)*Heaviside(t)+1/5*Heaviside(t)+
+34100/115861*sin(21/10*t)+775000/2433081*cos(21/10*t)+
+273403/579305*exp(-25/11*t)-83/105;
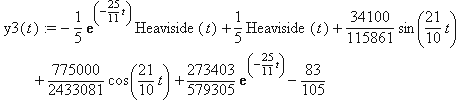
plot({y3(t)},t=0..20);
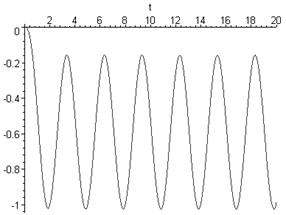
S(f):=(4.41-(2*Pi*f)^2)/(2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51-
-5*sqrt(-1)*(2*Pi*f)^3+22.05*2*Pi*f*sqrt(-1));
![]()
S(f):=(4.41-(2*Pi*f)^2)*((2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51) +
sqrt(-1)*(5*(2*Pi*f)^3+22.05*2*Pi*f))/ ((2.2*(2*Pi*f)^4-
-9.3*(2*Pi*f)^2+6.51)^2 -( sqrt(-1)*(5*(2*Pi*f)^3+
+22.05*2*Pi*f))^2);
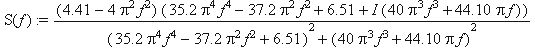
A(f):=(4.41-(2*Pi*f)^2)*(2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+
+6.51) / ((2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51)^2 -( sqrt(-
-1)*(5*(2*Pi*f)^3+22.05*2*Pi*f))^2);
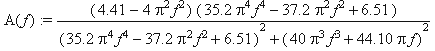
B(f):=(4.41-(2*Pi*f)^2)*(5*(2*Pi*f)^3+
+22.05*2*Pi*f) / ((2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51)^2 –
-( sqrt(-1)*(5*(2*Pi*f)^3+22.05*2*Pi*f))^2);

K(f):=sqrt( (A(f))^2+(B(f))^2 );
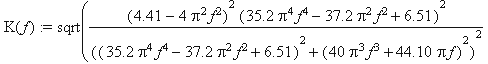
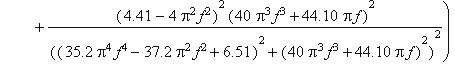
plot(K(f),f=0..1);
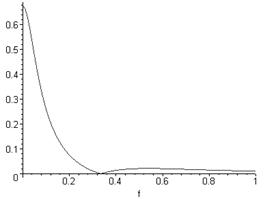
Q(f):=-arctan((B(f)/A(f)));
![]()
plot(Q(f),f=0..1);
Похожие работы
... ії (функціонали) обчислюються, як безперервні, а реально вони є дискретними (вимірювання здійснюються при дискретних значеннях фізичної величини - аргументу). Відмітною особливістю методичних похибок вимірювань є те, що вони, як правило, неконкретні і тому не можуть бути одержані будь-які узагальнені кількісні оцінки. Враховуючи це, методичні похибки звичайно не нормуються і не вказуються в техн ...
... . Частинну характеристику приймають такою, що задовольняє вимоги технічних умов, якщо максимальне значення із серії n її оцінок не перевищує допустимого значення. Нормування похибки взаємодії З усіх складових інструментальної похибки вимірювань найменш розроблені методи нормування похибки від взаємодії ЗВТ з ОВ. Згідно з фізичним походженням похибки взаємодії, для її оцінки необхідно ...
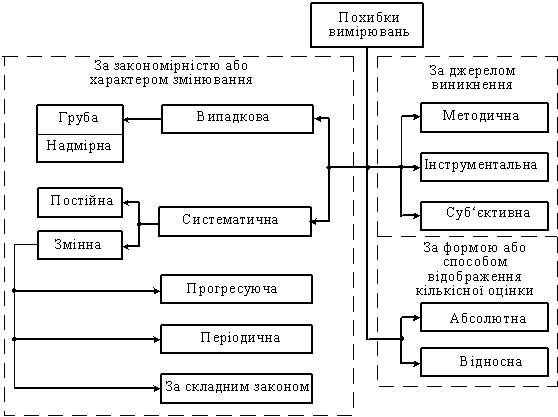
... живлення приладу. Сюди ж ставляться так називані промахи — похибки, пов'язані з помилковими діями спостерігача, — неправильне визначення показань приладу, невірний їхній запис і т.п. Результати вимірювань, що містять грубі похибки і промахи, відкидаються як явно неточні. Випадкова похибка - похибка вимірювання, викликана невідомими причинами або відомими причинами випадкового прояву. Випадкові ...
... є грубим. 2.8. Методи вилучення систематичних похибок з результатів вимірювань Систематичні похибки, незалежно від характеру їх змінювання в часі при постановці і проведенні вимірювального експерименту, повинні бути виявлені і вилучені з результатів вимірювань або хоча б зменшені, для чого важливо знати джерела і причини їх виникнення. За цією ознакою розрізняють такі систематичні похибки: ...
0 комментариев