Доказательство бесконечности некоторых видов простых чисел

Способ доказательства бесконечности количества некоторых видов простых чисел

Греческий ученый Евклид еще в ІІІ веке до нашей еры доказал, что количество простых чисел - бесконечено.

Теорема Дирихле утверждает, что в некоторой арифметической прогрессии, которая состоит с натуральных чисел, количество простых чисел или бесконечность. Это значит, если , тогда значения многочлена первой степени будут простыми числами при замене бесконечного количества целых чисел.

Уже о многочленах второй и о большей степени этого нельзя было сказать. Неразрешимой была проблема простых чисел-близнецов.

Ниже мы рассмотрим способ, с помощью которого можно решить часть этих проблем.

Рассмотрим многочлен который при значениях от  до , дает бесконечный ряд натуральных чисел  (1)

А также рассмотрим ряд простых чисел  (2) некоторого типа, о котором известно, что он бесконечен.

Пусть простые числа (2) делят числа (1) и некоторые числа (2) совпадают с некоторыми числами (1). Применяя способ решета Эратосфена, мы увидим, что каждое простое число  c (2) выбивает с ряда чисел (1) часть, а на все остальные простые числа останется  часть чисел (1).

Если p₁ выбивает t/ р₁ , то p₂ выбьет еще часть чисел (1) с тех, что осталась, а вместе они выбьют часть чисел(1).

Для всех остальных простых чисел останется

 

 

часть чисел (1)

Третье простое число  выбьет еще часть, а вместе они выбьют часть чисел (1). На все оставшиеся простые числа с (2) останется

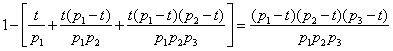
часть чисел (1)

Продолжая ми получим, что простые числа  выбивают

 (3)

часть чисел (1) , а на оставшиеся простые числа останется

 (4)

часть чисел (1)

Используем тот факт, что простые числа от  до  выбивают все сложные числа в интервале от  до .

Пусть наибольшее простое число с (2) совпадающее с последовательности (1). Для того чтобы выяснить, есть ли еще простые числа в последовательности (1) больше за  достаточно формулу (4) умножить на число А-количество чисел (1) на промежутке от  до  . И если

 (5)

значит, там еще есть простые числа больше  и меньше .

Рассмотрим проблему простых чисел-близнецов

Пусть многочлен первой степени ,где ,дает простые числа –близнецы. Требуется доказать, что их количество бесконечно. Запишем все пары чисел

 

    (6)

   

Легко показать, что каждое простое число выбивает по две пары таких чисел, то есть часть.

Пусть

 (7)

последняя известная нам пара простых чисел-близнецов этого вида. Используя формулы (3) мы увидим, что все простые числа от до  выбивают

 (8)

часть чисел (6). А , используя формулу (4) мы получим , что на все остальные простые числа останется

 

 (9)

часть чисел (6).

Для того, чтобы выяснить есть ли еще другие пары простых чисел-близнецов в последовательности (6) больше за (7), достаточно исследовать формулу (9) на промежутке до .

Если

 

 (10)

где А-количество пар чисел (6) на промежутке от  до ,тогда на этом промежутке есть еще хотя бы одна пара простых чисел-близнецов данного вида

Так как  

тогда последнее число вида (7) меньше , которое будет делиться простыми числами меньшими за  , будет число

 

.

С учетом этого формула (10) примет вид

 ,

где видно, что левая часть больше единицы, а это значит, что количество пар простых чисел-близнецов бесконечно.

Для примера рассмотрим простые числа-близнецы вида  .

Пусть наибольшая пара таких чисел. Так как числа такого вида нечетные, значит,  не принимает участия. Выражение (10) для данного случая примет вид , где очевидно, что оно больше единицы, а это значит, что количество пар простых чисел-близнецов вида бесконечно. Таким же способом можно рассматривать и более сложные многочлены первой степени. Очень легко доказывается и теорема Чебышева, Гольдбаха-Эйлера.

Рассмотрим многочлен второй степени

 

 (11)

Делителями его будут простые числа вида    (12)

Подставляя в (11) значения  от  до  получим ряд чисел  (13). Пускай наибольшее простое число вида . Требуется доказать что есть еще простые числа вида  больше за .

Каждое простое число (12) выбивает с последовательности (13)  часть чисел. С учетом формулы (3) мы получим, что все простые числа (12) от  до  выбивают

 (14)

часть чисел с последовательности (13) На остальные простые числа вида останется с учетом формулы (4)

 (15)

часть чисел последовательности (13).

Так как  ,тогда последнее число вида меньше , которое будет делиться простыми числами вида меньшим за , будет число  . .

Для того ,чтобы показать, что есть еще простые числа

 

 (16)

достаточно доказать, что

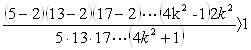 (17)

Для чего неравенство (17) запишем по-другому

 

 (18)

Рассматривая (18), видим, что оно больше за единицу. Это значит что утверждение (16) верно, а значит, и количество простых чисел вида  бесконечно.