Навигация
Экстраполяция тенденции как метод прогнозирования
15840
знаков
0
таблиц
0
изображений
2.1 Экстраполяция тенденции как метод прогнозирования
Основа большинства методов прогнозирования - экстраполяция тенденции, связанная с распространением закономерностей, связей и соотношений, действующих в изучаемом периоде, за его пределы или, другими словами, это получение представлений о будущем на основе информации, относящейся к прошлому и настоящему.
Экстраполяция, проводимая в будущее,- это перспектива, а в прошлое,- ретроспектива.
Предпосылки применения экстраполяции:
· развитие исследуемого явления в целом следует описывать плавной кривой;
· общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьезных изменений в будущем.
Экстраполяцию в общем виде можно представить так:
,
где 
- прогнозируемый уровень; 
- текущей уровень прогнозного ряда;
Т- срок экстраполяции; 
- параметр уравнения тренда.
При этом могут использоваться разные методы в зависимости от исходной информации.
Упрощенные приемы целесообразны при недостаточной информации о предыстории развития явления (нет достаточно длинного ряда или информация заданна только двумя точками: на начало и конец периода). Упрощенные приемы основываются на средних показателях динамики, и можно выделить:
1. Метод среднего абсолютного прироста.
Для нахождения интересующего нас аналитического выражения тенденции на любую дату необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд.
,
где t- срок прогноза; i- номер последнего уровня.
Применение в экстраполяции среднего абсолютного прироста предполагает, что развитие явления происходит по арифметической прогрессии и относится в прогнозировании к классу «наивных» моделей, ибо чаше всего развитие явления следует по иному пути, чем арифметическая прогрессия Т.С. Вместе с тем в ряде случаев этот метод может найти применение как предварительный прогноз, если у исследователя нет динамического ряда: информация дана лишь на начало и конец периода (например, данные одного баланса).
2. Метод среднего темпа роста.
Осуществляется, когда общая тенденция характеризуется показательной кривой
,
где 
- последний уровень ряда динамики; k- средний коэффициент роста.
3. Выравнивание рядов по какой-либо аналитической формуле.
Экстраполяция дает возможность получить точечное значение прогнозов. Точное совпадение фактических данных и прогнозных точечных оценок, полученных путем экстраполяции кривых, имеет малую вероятность.
Любой статистический прогноз носит приближенный характер, поэтому целесообразно определение доверительных интервалов прогноза:
, 
,
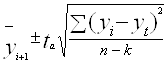где 
- коэффициент доверия по распределению Стьюдента при уровне значимости 
; 
- средняя квадратическая ошибка тренда; k- число параметров в уравнении; 
- расчетное значение уровня.
Аналитические методы основаны на применении метода наименьших квадратов к динамическому ряду и представлении закономерности развития явления во времени в виде уравнения тренда, то есть математической функции уровней динамического ряда (y) от факторного времени (t): y=f(t).
Аналитическое сглаживание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых нет исходных данных.
Адаптивные методы используются в условиях сильной колеблемости уровней динамического ряда и позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда. К адаптивным методам относятся методы скользящих и экспоненциальных средних, метод гармонических весов, методы авторегрессионных преобразований.
Цель адаптивных методов заключается в построении самонастраивающихся моделей, способных учитывать информационную ценность различных членов временного ряда и давать достаточно точные оценки будущим членам данного ряда. ТС
Прогноз получается как экстраполяция последней тенденции. В разных методиках прогнозирования процесс настройки (адаптации) модели осуществляется по-разному, и можно выделить:
1) метод скользящей средней (адаптивной фильтрации, метод Бонса-Дженкинса);
2) метод экспоненциального сглаживания (методы Хольда, Брауна, экспоненциальной средней).
Скользящие средние представляют собой средние уровни за определенные периоды времени путем последовательного передвижения начала периода на единицу времени. При простой скользящей средней все уровни временного ряда считаются равноценными, а при исчислении взвешенной скользящей средней каждому уровню в пределах интервала сглаживания приписывается вес, зависящий от расстояния данного уровня до середины интервала сглаживания.
Особенность метода экспоненциального сглаживания в том, что в процедуре выравнивания каждого наблюдения используется только значения предыдущих уравнений, взятых с определенным весом. Смысл экспоненциальных средних состоит в нахождении таких средних, в которых влияние прошлых наблюдений затухает по мере удаления от момента, для которого определяется средние.
Заключение
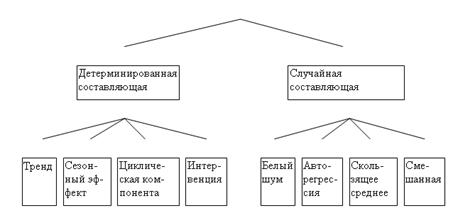
Для временных рядов главный интерес представляет описание или моделирование их структуры. Цель таких исследований, как правило, шире моделирования, хотя некоторую информацию можно получить и непосредственно из модели, делая выводы о выполнении тех или иных экономических законов (скажем, закона паритета покупательной способности) и проверяя различные гипотезы. Построенная модель может использоваться для экстраполяции или прогнозирования временного ряда, и тогда качество прогноза может служить полезным критерием при выборе среди нескольких моделей. Построение хороших моделей ряда необходимо и для других приложений, таких, как корректировка сезонных эффектов и сглаживание. Наконец, построенные модели могут использоваться для статистического моделирования длинных рядов наблюдений при исследовании больших систем, для которых временной ряд рассматривается как входная информация.
Список литературы
1. А.О. Крыштановский. Методы анализа временных рядов // Мониторинг общественного мнения: экономические и социальные перемены. 2000. № 2 (46). С. 44-51. [Статья]
2. Прогнозирование и планирование в условиях рынка: Учеб. пособие для Вузов / Под. ред. Т.Г. Морозовой, А.В. Пикулькина. – М.: ЮНИТИ – ДАНА, 1999.
3. Бокс Дж., Дженкинс Г. (1974) Анализ временных рядов. Прогноз и управление. - М.: Мир, 1974. - Вып. 1, 2.
Похожие работы
... последовательность случайные величины распределены одинаково, так что определенный выше процесс белого шума является стационарным. 7.Числовые характеристики случайной составляющей При анализе временных рядов используются числовые характеристики, аналогичные характеристикам случайных величин: – математическое ожидание (среднее значение процесса) ; – автоковариационная функция ; ...
... временного ряда и объяснение механизма формирования ряда часто используются для статистического прогнозирования, которое в большинстве случаев сводится к экстраполяции обнаруженных тенденций развития. Анализ временного ряда и последующее прогнозирование его развития может использоваться для: – планирования в экономике, производстве, торговле; – управления и оптимизации, протекающих в обществе ...
... величины могут быть разнородными (иметь различную физическую, экономическую или математическую природу). Коллокационная модель может быть использована не только для построения оптимального прогноза однородных данных, но и для оценивания любых интересующих характеристик финансовых инструментов фондового рынка по неоднородной исходной информации (доходностей, курсов, объемов продаж, индексов и ...
... развитие экспертное прогнозирование, ориентированное в большей степени на работу не только с количественной, но и с качественной информацией, получаемой непосредственно от экспертов. 2. Метод экспертного прогнозирования. С помощью этого метода прогнозирования может быть решена большая часть проблем, возникающих при разработке прогнозов. В экспертном прогнозировании существует несколько основных ...
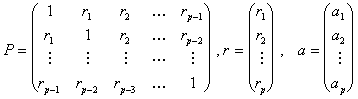
0 комментариев