Навигация
Моделирование систем массового обслуживания
4. Моделирование систем массового обслуживания
Многие экономические задачи связаны с системами массового обслуживания (СМО), т. е. такими системами, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, с другой — происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающие устройства (каналы обслуживания), выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания.
Методами теории массового обслуживания могут быть решены многие задачи исследования процессов, происходящих в экономике. Так, в организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Другим характерным примером систем массового обслуживания могут служить склады или базы снабженческо-сбытовых организаций, и задача теории массового обслуживания в данном случае сводится тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными. Теория массового обслуживания может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку — как требования. Модели теории массового обслуживания применяются также при решении ряда задач организации и нормирования труда, других социально-экономических проблем.
Системы массового обслуживания могут быть классифицированы по ряду признаков.
1. В зависимости от условий ожидания начала обслуживания различают:
• СМО с потерями (отказами),
• СМО с ожиданием.
В СМО с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и теряются. Классическим примером системы с отказами является телефонная станция. Если вызываемый абонент занят, то требование на соединение с ним получает отказ и теряется.
В СМО с ожиданием требование, застав все обслуживающие каналы занятыми, становится в очередь и ожидает, пока не освободится один из обслуживающих каналов.
СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ограниченной длинной очереди.
СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.
2. По числу каналов обслуживания СМО делятся на:
одноканальные;
многоканальные.
3. По месту нахождения источника требований МО делятся на:
- разомкнутые, когда источник требования находится вне системы;
- замкнутые, когда источник находится в самой системе.
Примером разомкнутой системы может служить ателье по ремонту телевизоров. Здесь неисправные телевизоры — это источник требований на их обслуживание, находятся вне самой системы, число требований можно считать неограниченным. К замкнутым СМО относится, например, станочный участок, в котором станки являются источником неисправностей, а следовательно, источником требований на их обслуживание, например, бригадой наладчиков
Возможны и другие признаки классификации СМО, например, по дисциплине обслуживания, однофазные и многофазные СМО и др.
Методы и модели, применяющиеся в теории массового обслуживания, можно условно разделить на аналитические имитационные.
Аналитические методы теории массового обслуживания позволяют получить характеристики системы как некоторые функции параметров её функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО. Имитационные методы основаны на моделировании процессов массового обслуживания на ЭВМ и применяются, если, невозможно применение аналитических моделей. Далее будем рассматривать аналитические метод моделирования СМО.
В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых входящий поток требований является простейшим (пуассоновским).
Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т.е. вероятность поступления за время t ровно k требований задается формулой:
![]()
Простейший поток обладает тремя основными свойств ординарности, стационарности и отсутствием последствия.
Ординарность потока означает практическую невозможность одновременного поступления двух и более требований. Например, достаточно малой является вероятность того, что из группы станков, обслуживаемых бригадой ремонтников, одновременно выйдут из строя сразу несколько станков.
Стационарным называется поток, для которого математическое ожидание числа требований, поступающих в систему в единицу времени (обозначим ![]() ), не меняется во времени. Таким образом, вероятность поступления в систему определенного количества требований в течение заданного промежутка времени
), не меняется во времени. Таким образом, вероятность поступления в систему определенного количества требований в течение заданного промежутка времени ![]() t зависит от его величины и не зависит от начала его отсчета на оси времени.
t зависит от его величины и не зависит от начала его отсчета на оси времени.
Отсутствие последействия означает, что число требований, поступивших в систему до момента t, не определяет того сколько требований поступит в систему за промежуток времени от t до t+![]() t.
t.
Важная характеристика СМО — время обслуживания требований в системе. Время обслуживания одного требования является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и особенно в практических приложениях получил экспоненциальный закон распределения
времени обслуживания. Функция распределения для этого она имеет вид:
![]()
т.е. вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой, где ![]() — параметр экспоненциального закона распределения времени обслуживания требований в системе, т.е. величина, обратная среднему времени обслуживания
— параметр экспоненциального закона распределения времени обслуживания требований в системе, т.е. величина, обратная среднему времени обслуживания ![]() :
:
![]()
![]()
Рассмотрим аналитические модели наиболее распространенных СМО с ожиданием, т.е. таких СМО, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, ставятся в очередь и обслуживаются по мере освобождения каналов.
Общая постановка задачи состоит в следующем. Система имеет n обслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование.
В систему поступает простейший (пуассоновский) поток лини с параметром ![]() . Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.
. Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.
Время обслуживания каждого требования ![]() — случайная величина, которая подчиняется экспоненциальному закону распределения с параметром
— случайная величина, которая подчиняется экспоненциальному закону распределения с параметром ![]() .
.
СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. К замкнутым относятся системы, в которых поступающий поток требований возникает в самой системе и ограничен.
Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Отмеченные особенности функционирования этой системы. Расчет характеристик работы СМО различного вида может быть проведен на основе расчета вероятностей состояний СМО (так называемы формулы Эрланга).
Рассмотрим алгоритмы расчета показателей качества функционирования разомкнутой системы массового обслужит с ожиданием.
При изучении таких систем рассчитывают различны показатели эффективности обслуживающей системы. В качестве![]() основных показателей могут быть вероятность того, что все каналы свободны или заняты, математическое ожидание длины очереди (средняя длина очереди), коэффициент занятости и простоя каналов обслуживания и др.
основных показателей могут быть вероятность того, что все каналы свободны или заняты, математическое ожидание длины очереди (средняя длина очереди), коэффициент занятости и простоя каналов обслуживания и др.
Введем в рассмотрение параметр ![]() . Заметим, что если
. Заметим, что если ![]() , то очередь не может расти безгранично. Это условие имеет следующий смысл:
, то очередь не может расти безгранично. Это условие имеет следующий смысл: ![]() — среднее число требований, поступающих за единицу времени,
— среднее число требований, поступающих за единицу времени, ![]() -время обслуживания одним каналом одного требования. Тогда
-время обслуживания одним каналом одного требования. Тогда ![]() — среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступившие требования. Поэтому условие
— среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступившие требования. Поэтому условие ![]() < 1 означает, что число обслуживающих каналов должно быть больше числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования. Важнейшие характеристики работы СМО:
< 1 означает, что число обслуживающих каналов должно быть больше числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования. Важнейшие характеристики работы СМО:
1. Вероятность того, что все обслуживающие каналы свободны
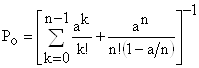
2. Вероятность того, что занято ровно k обслуживающих каналов при условии, что общее число требований, находятся на обслуживании, не превосходит числа обслуживающих аппаратов:
![]() Poгде
Poгде ![]()
3. Вероятность того, что в системе находится k требований в случаи, когда их число больше числа обслуживающих каналов:
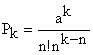 где
где ![]()
4. Вероятность того, что все обслуживающие каналы заняты:
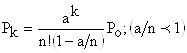
5.Среднее время ожидания требованием начала обслуживания в системе:
![]()
6.Средняя длина очереди:

7.Среднее число свободных от обслуживания каналов:

8.Коэффициент простоя каналов:
![]() .
.
9.Среднее число занятых обслуживанием каналов:
![]()
10.Коэффициент загрузки каналов:
![]()
Перейдем к рассмотрению алгоритмов расчета характеристик функционирования замкнутых СМО. Поскольку система замкнутая, то к постановке задачи следует добавить условие: поток поступающих требований ограничен, т.е. в системе обслуживания одновременно не может находиться больше m требований (m — число обслуживаемых объектов).
За критерий, характеризующий качество функционирования рассматриваемой системы, выберем отношение средней длины очереди к наибольшему числу требований, находящихся одновременно в обслуживающей системе — коэффициент простоя обслуживаемого объекта. В качестве другого критерия возьмем отношение среднего числа незанятых обслуживающих каналов к их общему числу — коэффициент простоя обслуживаемого канала.
Первый из названных критериев характеризует потери времени из-за ожидания начала обслуживания; второй показывает полноту загрузки обслуживающей системы.
Очевидно, что очередь может возникнуть, лишь когда число каналов меньше наибольшего числа требований, находящихся одновременно в обслуживающей системе (n < m).
Приведем последовательность расчетов характерней замкнутых СМО и необходимые формулы.
1. Определим параметр ![]() — показатель загрузки системы, т.е. математическое ожидание числа требований поступающих в систему за время, равное средней длительности обслуживания (
— показатель загрузки системы, т.е. математическое ожидание числа требований поступающих в систему за время, равное средней длительности обслуживания (![]() ).
).
2. Вероятность того, что занято k обслуживающих каналов при условии, что число требований, находящихся в системе не превосходит числа обслуживающих каналов системы:
![]()
3. Вероятность того, что в системе находится k требований для случая, когда их число больше числа обслуживающих каналов:
![]()
4. Вероятность того, что все обслуживающие каналы свободны, определим, используя очевидное условие:
 , откуда
, откуда 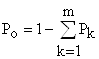 .
.
Величину Ро можно получить также путем подстановки в равенство ![]() значения
значения ![]() , в которых Ро вводит сомножителем. Подставляя их, получаем следующее уравнение для определения Ро:
, в которых Ро вводит сомножителем. Подставляя их, получаем следующее уравнение для определения Ро:
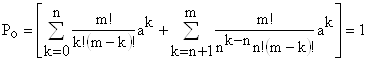 ,
,
откуда

5.Среднее число требований, ожидающих начала обслуживания (средняя длина очереди),
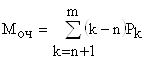
или
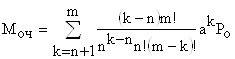 .
.
6.Коэффициент простоя обслуживаемого требования ( объекта)
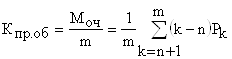 .
.
7. Среднее число требований, находящихся в обслуживающей системе, обслуживаемых и ожидающих обслуживания:
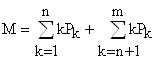
или
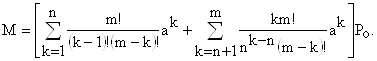
8.Среднее число свободных обслуживающих каналов
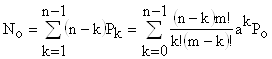 .
.
9.Коэффициент простоя обслуживающего канала:
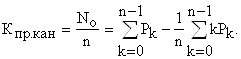
II. Практическое применение теории игр в задачах моделирования экономических процессах
Пример №1
На базе торговой фирмы имеется n типов товара ассортиментного минимума. В магазин фирмы должен быть завезен только один из этих типов товара. Если товар типа j![]() будет пользоваться спросом, то магазин от его реализации получит прибыль
будет пользоваться спросом, то магазин от его реализации получит прибыль ![]() . Если же этот товар не будет пользоваться спросом, то издержки на его хранение принесут магазину убыток
. Если же этот товар не будет пользоваться спросом, то издержки на его хранение принесут магазину убыток ![]() .Требуется выбрать тип товара, который целесообразно завезти в магазин.
.Требуется выбрать тип товара, который целесообразно завезти в магазин.
В условиях неопределенного покупательского спроса конфликтная ситуация товароснабжения формализуется матричной игрой. Пусть первый игрок — магазин, второй игрок — покупательский спрос. Каждый из игроков имеет по n стратегий. Завоз i-го товара — i-я. стратегия первого игрока, спрос на j-й товар — j-я стратегия второго игрока. Тогда матрица выигрышей первого игрока имеет вид квадратной матрицы n-го порядка:
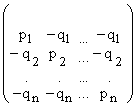
Пример №2
Матрица игры имеет вид:

Минимальный элемент первой строки (первой стратегии первого игрока) равен 2, второй — 5, третьей — 4; максимальное значение из этих величин равно 5. Максимальный элемент первого столбца (первой стратегии второго игрока) равен 10, второго — 10; третьего — 5, четвертого — 14, пятого — 12; минимальное значение из них равно 5. Следовательно, данная игра имеет седловую точку (2, 3) и задача разрешима в чистых стратегиях. Придерживаясь чисто второй стратегии, первый игрок обеспечивает себе выигрыш, не меньший 5; второй игрок, применяя чистую третью стратегию, проигрывает не более 5. Обе стратегии j = 2 и j = 3 являются оптимальными для первого и второго игроков, при этом цена игры V = 5.
Пример №3
Диспетчер автобусного парка (ЛПР) в месяцы в конце каждой недели должен принять решение о целесообразности выделения дополнительных автобусов на загородный маршрут. ЛПР имеет три варианта решений: увеличить количество автобусов на 10 (стратегия ![]() ) увеличить это количество на 5 (стратегия Р2) или оставить без изменения обычное число автобусов на линии (стратегия Р3). Возможны два состояния погоды: —Q1 плохая погода,Q2 - хорошая погода, причем в момент принятия решения нет возможности определить ожидаемое состояние погоды. Если в выходные дни будет хорошая погода и много желающих выехать за город, а выделено мало автобусов, то парк понесет убытки, связанные с недополученной прибылью. Если же выделены дополнительные автобусы, а погода окажется плохой, то возникнут потери вследствие эксплуатации незаполненных автобусов.
) увеличить это количество на 5 (стратегия Р2) или оставить без изменения обычное число автобусов на линии (стратегия Р3). Возможны два состояния погоды: —Q1 плохая погода,Q2 - хорошая погода, причем в момент принятия решения нет возможности определить ожидаемое состояние погоды. Если в выходные дни будет хорошая погода и много желающих выехать за город, а выделено мало автобусов, то парк понесет убытки, связанные с недополученной прибылью. Если же выделены дополнительные автобусы, а погода окажется плохой, то возникнут потери вследствие эксплуатации незаполненных автобусов.
Пусть, на основе анализа статистических данных за определенный период установлена функция потерь для возможных комбинаций состояний природы и решений ЛПР в виде матрицы игры А (Рi,Qi), в которой отрицательные значения показывают дополнительную прибыль, а положительные – потери:
Q1 Q2
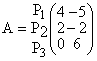
Если нет сведений о вероятностях различных состояний погоды, то по критерию Вальда и по критерию Сэвиджа оптимальной является стратегия Р2. По критерию Гурвица при “коэффициенте пессимизма” q=1 оптимальной окажется стратегия Р2, а при q=0 — стратегия Р1.
Пример №4
Швейное предприятие, выпускающее детские платья и костюмы, реализует свою продукцию через фирменный магазин. Сбыт продукции зависит от состояния погоды. Но данным прошлых наблюдений предприятие в течении апреля — мая в условиях теплой погоды может реализовать 600 костюмов и 1975 платьев, а при прохладной погоде 1000 костюмов и 625 платьев. Известно, что затраты на единицу продукции в течение указанных месяцев составили для костюмов 27 руб., для платьев 8 руб., а цена реализации равна соответственно 48 руб. и 16 руб. (цифры условные).
Задача заключается в максимизации средней величины прибыли от реализации выпущенной продукции с учетом неопределенности погоды в рассматриваемые месяцы. Таким образом, служба маркетинга предприятия должна в этих условиях определить оптимальную стратегию предприятия, обеспечивающую при любой погоде определенный средний доход. Решим эту задачу методами теории игр, игра в этом случае будет относиться к типу игр с природой.
Предприятие располагает в этих условиях двумя чистыми стратегиями: стратегия А — в расчете на теплую погоду и стратегия Б — в расчете на холодную погоду. Природу будим рассматривать как второго игрока также с двумя стратегиями: прохладная погода (стратегия В) и теплая погода (стратегия Г). Если предприятие выберет стратегию А, то в случае прохладной погоды (стратегия природы В) доход составит
600(48 - 27) + 625(16 - 8) - (1975 - 625)8 = 6 800 руб.,
а в случае теплой погоды (стратегия природы Г) доход равен
600(48 - 27) + 1 975(16 - 8) = 28 400 руб.
Если предприятие выберет стратегию Б, то реализация продукции в условиях прохладной погоды даст доход
1 000(48 - 27) + 625(16 - 8) = 26 000 руб.,
а в условиях теплой погоды
600(48 - 27) + 625(16 - 8) - (1 000 - 600)27 = 6 800
Следовательно, матрица данной игры (платежная матица) имеет вид:
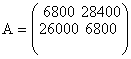
Первая и вторая строки этой матрицы соответствуют стратегиям А и Б предприятия, а первый и второй стратегиям В и Г природы.
По платежной матрице видно, что первый игрок (предприятие) никогда не получит доход меньше 6800. Но если погодные условия совпадают с выбранной стратегией, то выручка (выигрыш) составит 26 000 или 28 400. Отсюда можно сделать вывод, что в условиях неопределенности погоды наибольший гарантированный доход предприятие обеспечит, если будет попеременно применять то А, то стратегию Б. Такая стратегия называется смешанной. Оптимизация смешанной стратегии позволит первому игроку всегда получать выигрыша независимо от стратегии второго игрока.
Пусть х означает частоту применения первым игроком стратегии А, тогда частота применения им стратегии Б равна (1 - х). В случае оптимальной смешанной стратегии первый игрок (предприятие) получит и при стратегии В (холодная погода), и при стратегии Г (теплая погода) второго игрока одинаковый средний доход:
6800х + 26 000(1 - х) = 28 400х + 6800(1 - х).
Отсюда можно найти, что х — 8/17; 1 - х = 9/17.
Следовательно, первый игрок, применяя чистые стратеги А и Б в соотношении 8:9, будет иметь оптимальную смешанную стратегию, обеспечивающую ему в любом случае средний доход в сумме
6800-8/17 + 26000-9/17 ![]() 16965 руб.; эта величина и будет в данном случае ценой игры.
16965 руб.; эта величина и будет в данном случае ценой игры.
Легко рассчитать, какое количество костюмов и платьев должно выпускать предприятие при оптимальной стратегии:
(600 костюмов + 1975 платьев)*8/17 + (1000 костюмов + 625 платьев)*9/17 = 812 костюмов + 1260 платьев.
Следовательно, оптимальная стратегия предприятия заключи в выпуске 812 костюмов и 1260 платьев, что обеспечит три любой погоде средний доход в сумме 16 965 руб.
Заключение
На основании выше изложенного материала можно сделать вывод о том, что особое внимание при исследовании экономико-математических методов необходимо уделять следующим моментам:
- фактору сезонности в экономических процессах;
- приведению формул и примеров расчетов;
- рассмотрению ряда прикладных задач маркетинга, менеджмента и других областей управления в экономике;
- моделированию спроса и потребления;
- научному управлению запасами;
- анализу сетевого планирования и управления;
- анализу динамического программирования;
- аналитическому моделированию систем массового обслуживания;
- принятию решений на основе теории игр.
Так как я в своей работе особое внимание уделила теории игр, то, после рассмотрения ее более подробно, и в этой конкретной области можно сделать определенные выводы. Здесь представлены, на мой взгляд, более актуальные задачи:
- как сделать так, чтобы природа работала на тебя, а не ты на неё;
- как получить набольшую выгоду или учет твоих интересов конкурентом, или поставщиком;
- какой товар лучше производить и т.д.
Список используемой литературы
1. Экономико-математические методы и прикладное моделирование / В.В. Федосеев. – М.: ЮНИТИ, 2002. - 391 с.
2. Математическое моделирование макроэкономических процессов / А.Н. Котов. – Л.: ЛГУ, 1980
3. Основы экономико-математического моделирования / Ю.Г. Семенов.1976
4. Экономико-математические методы / Л.Л. Терехов.– М.: Статистика–1972
Похожие работы
... систем стимулирования. Она полезна также для формирования и развития внутрифирменных культур. Важный вклад в использование теории игр вносят экспериментальные работы. Многие теоретические выкладки отрабатываются в лабораторных условиях, а полученные результаты служат импульсом для практиков. Теоретически было выяснено, при каких условиях двум эгоистически настроенным партнерам целесообразно ...
... налогов; при разработке мер государственного воздействия по регулированию выпуска сельскохозяйственной продукции; установление минимума заработной платы, и т.д. 2. Варианты практического применения теории эластичности Теория эластичности спроса и предложения имеет важное практическое значение. Для фирмы важно иметь в виду, что эластичность спроса на ее продукцию и эластичность рыночного ...
... смешанными стратегиями игроков 1 и 2 называются такие наборы хо, уо соответственно, которые удовлетворяют равенству Е (А, х, y) = Е (А, х, y) = Е (А, хо, уо). Величина Е (А, хо ,уо) называется при этом ценой игры и обозначается через u. Имеется и другое определение оптимальных смешанных стратегий: хо, уо называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они ...
... , и он не делает реальных попыток переступить границы того, что многие считают настоящей психологической наукой. Таким образом, следуя бихевиористской традиции, из которой отчасти вышла социально-когнитивная теория, Бандура строго привержен положению, что природа человека, в конечном счете, познаваема наукой. Социально-когнитивная теория хорошо обоснована в эмпирических исследованиях. К их ...



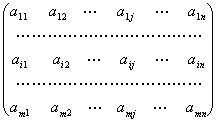
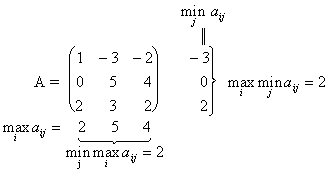
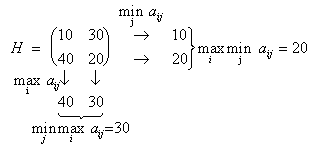




0 комментариев