Навигация
Определение статистических показателей производства
Задача 1. Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности
| Номер завода | Среднегодовая стоимость ОПФ, млн.руб. | Валовая продукция в сопоставимых ценах, млн. руб. |
| 1 | 3,4 | 3,5 |
| 2 | 3,1 | 3,3 |
| 3 | 3,5 | 3,5 |
| 4 | 4,1 | 4,5 |
| 5 | 5,8 | 7,5 |
| 6 | 5,2 | 6,9 |
| 7 | 3,8 | 4,3 |
| 8 | 4,1 | 5,9 |
| 9 | 5,6 | 4,8 |
| 10 | 4,5 | 5,8 |
| 11 | 4,2 | 4,5 |
| 12 | 6,1 | 8,4 |
| 13 | 6,5 | 7,3 |
| 14 | 2,0 | 2,1 |
| 15 | 6,4 | 7,8 |
| 16 | 4,0 | 4,2 |
| 17 | 8,0 | 10,6 |
| 18 | 5,1 | 5,8 |
| 19 | 4,9 | 5,3 |
| 20 | 4,3 | 4,9 |
| 21 | 5,8 | 6,0 |
| 22 | 7,2 | 10,4 |
| 23 | 6,6 | 6,9 |
| 24 | 3,0 | 3,5 |
| 25 | 6,7 | 7,2 |
С целью изучения зависимости между среднегодовой стоимостью ОПФ и выпуском валовой продукции производите группировку заводов по среднегодовой стоимости ОПФ, образовав 4 группы заводов с равными интервалами. По каждой группе и совокупности заводов подсчитайте:
1. число заводов;
2. среднегодовую стоимость ОПФ – всего и в среднем за один год;
3. стоимость валовой продукции - всего и в среднем за один год;
4. размер валовой продукции на один рубль ОПФ (фондоотдачу);
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Решение
Величина интервала определяется по формуле:
i=R/m, где R- размах колебания признака;
R= xmax– xmin, где xmax,
xminсоответственно максимальное и минимальное значение признака в совокупности;
m- число групп.
i = (xmax– xmin)/m = (8,0 – 2,0) / 4 = 6/4 = 1,5
| Группы заводов | Число заводов | Среднегодовая стоимость ОПФ, млн.руб. | Стоимость валовой продукции, млн.руб. | Фондоотдача (гр.6 / гр. 4) | ||
| Всего | В среднем за год | Всего | В среднем за год | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 – 3,5 | 5 | 15 | 3 | 15,9 | 3,18 | 1,06 |
| 3,5 – 5,0 | 8 | 33,9 | 4,2375 | 39,4 | 4,925 | 1,162 |
| 5,0 – 6,5 | 8 | 46,5 | 5,8125 | 54,5 | 6,8125 | 1,172 |
| 6,5 – 8,0 | 4 | 28,5 | 7,125 | 35,1 | 8,775 | 1,232 |
Выводы: Как видно по данным, представленным в таблице наиболее высокие показатели среднегодовой стоимости ОПФ, стоимости валовой продукции и фондоотдачи прослеживаются по 3 группе заводов и минимальные показатели по 1 группе.
Задача 2. Имеются следующие данные по зерновым культурам:
| Культура | В отчетном периоде | План на предстоящий период | ||
| Урожайность, ц/га | Валовой сбор, ц | Урожайность, ц/га | Посевная площадь, га | |
| Пшеница | 21,0 | 63 000 | 23,0 | 3 300 |
| Ячмень | 19,0 | 38 000 | 20,0 | 1 800 |
Вычислите среднюю урожайность зерновых культур:
Похожие работы
... , табличные характеристики связи. Это в свою очередь потребовало решения соответственно теоретико-методологических проблем. Глава 2. Абсолютные и относительные величины 2.1. Понятие, формы выражения и виды статистических показателей Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом и анализом различных по виду и форме выражения статистических ...
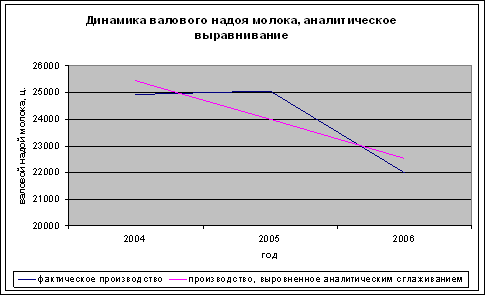
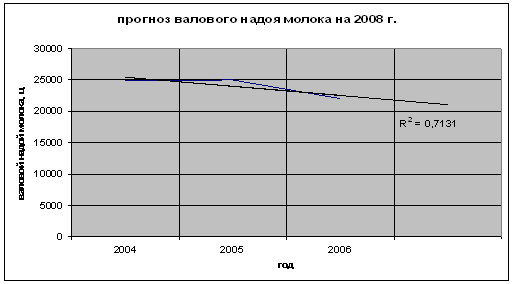
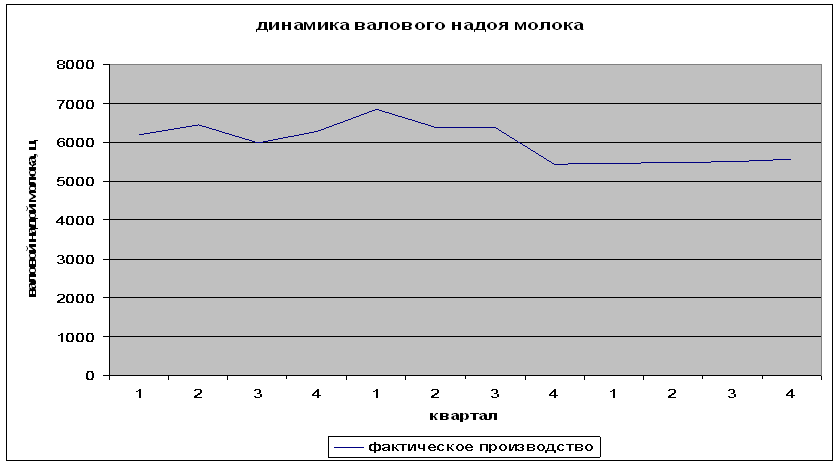
... в 2005году и высокая рентабельность продукции – 42,44% и продаж – 29,79%. В 2006 году отмечается спад прибыли от продаж продукции, а также снижение рентабельности продукции и продаж. 3.Экономико-статистический анализ производства продукции В решении задач, поставленных перед животноводством, большая роль принадлежит статистике. Статистика животноводства прежде всего должна правдиво, глубоко и ...
... 0,9 -0,3 Фондоемкость, руб. 0,8 1,0 1,1 +0,3 Производительность труда, тыс. руб. 303,0 310,0 359,7 +56,7 Уровень рентабельности, % +5,7 +7,8 +10 +4,3 3. Экономико-статистический анализ производства сахарной свеклы Экономико-статистический анализ заключается во всестороннем изучении состояния сельского хозяйства, с тем, чтобы сделать выводы о закономерностях его развития и ...
... выработки, не включаемых в стоимость продукции, и добавить прирост или вычесть уменьшение остатка по счету «Резерв предстоящих расходов и платежей». [23, с. 186] 1.2 Динамики производственных затрат на производство зерна, сахарной свеклы, подсолнечника за 6 лет Произведем анализ динамики производственных затрат зерна, сахарной свеклы и подсолнечника за 6 лет. Исходные данные приведены в ...
0 комментариев