Задаем характеристики исследуемого предприятия. Веса показателям устанавливаются экспертами

2. Задаем характеристики исследуемого предприятия. Веса показателям устанавливаются экспертами.

	s	n
Показатели	Исследуемое предприятие	Вектор весов показателей (выбирается экспертами)
Коэф. абсолютной ликвидности	0,57	9
Коэф. оборачиваемости собст-венных средств	0.49	3
Коэф. обеспеченности денежных средств и расчетов	0,53	7
Рентабельность использования всего капитала	2,4	4
Рентабельность продаж	1,8	5

3. Рассчитываем разницу между составляющими векторов исследуемого предприятия и каждого эталонного образа:

(s-xi)
0,39	0,33	0,19	0,10
-0,22	-0,36	-0,47	-1,21
0,50	0,45	0,39	0,32
2,38	2,31	2,28	2,21
1,75	1,66	1,54	1,49

4. Рассчитываем квадрат разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

(s-xi)^2
0,1521	0,1089	0,0361	0,0100
0,0484	0,1296	0,2209	1,4641
0,2500	0,2025	0,1521	0,1024
5,6644	5,3361	5,1984	4,8841
3,0625	2,7556	2,3716	2,2201

 5. Таким образом, расстояния по Эвклиду (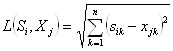) между исследуемым предприятием и эталонными образами будут равны:

	х1	х2	х3	х4
Расстояния по Эвклиду	9,1774	8,5327	7,9791	8,6807

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).

6. Рассчитываем разницу между составляющими векторов исследуемого предприятия и каждого эталонного образа, возведенную в степень λ=4:

(s-xi)^λ, λ=4
0,02313441	0,01185921	0,00130321	0,00010000
0,00234256	0,01679616	0,04879681	2,14358881
0,06250000	0,04100625	0,02313441	0,01048576
32,08542736	28,47396321	27,02336256	23,85443281
9,37890625	7,59333136	5,62448656	4,92884401

7. Таким образом, расстояния по Минковскому () между исследуемым предприятием и эталонными образами будут равны:

	х1	х2	х3	х4
Расстояние по Минковскому	41,55231058	36,13695619	32,72108355	30,93745139

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

8. Рассчитываем модуль разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

|s-xi|
0,39	0,33	0,19	0,10
0,22	0,36	0,47	1,21
0,50	0,45	0,39	0,32
2,38	2,31	2,28	2,21
1,75	1,66	1,54	1,49

9. Таким образом, расстояния по модулю разницы () между исследуемым предприятием и эталонными образами будут равны:

	х1	х2	х3	х4
Расстояние по модулю разности	5,24	5,11	4,87	5,33

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).

10. Рассчитываем произведение весов коэффициентов и квадрата разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

nj*(s-xi)^2
1,0647	0,7623	0,2527	0,0700
0,2904	0,7776	1,3254	8,7846
0,7500	0,6075	0,4563	0,3072
22,6576	21,3444	20,7936	19,5364
15,3125	13,7780	11,8580	11,1005

11. Таким образом, расстояния по Эвклиду с весами () между исследуемым предприятием и эталонными образами будут равны:

	х1	х2	х3	х4
Расстояние по Эвклиду (c весами)	40,0752	37,2698	34,6860	39,7987

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).

12. Рассчитываем произведение весов коэффициентов и разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа, возведенной в степень λ=4:

nj*(s-xi)^λ, λ=4
0,16194087	0,08301447	0,00912247	0,0007
0,01405536	0,10077696	0,29278086	12,86153286
0,1875	0,12301875	0,06940323	0,03145728
128,3417094	113,8958528	108,0934502	95,41773124
46,89453125	37,9666568	28,1224328	24,64422005

13. Таким образом, расстояния по Минковскому с весами (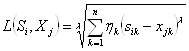) между исследуемым предприятием и эталонными образами будут равны:

	х1	х2	х3	х4
Расстояние по Минковскому (c весами)	175,5997369	152,1693198	136,5871896	132,9556414

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

14. Рассчитываем произведение весов коэффициентов и модулей разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

nj*|s-xi|
2,73	2,31	1,33	0,7
1,32	0,4752	0,223344	0,27024624
1,5	1,35	1,17	0,96
9,52	9,24	9,12	8,84
8,75	8,3	7,7	7,45

15. Таким образом, расстояния по модулю разницы с весами () между исследуемым предприятием и эталонными образами будут равны:

	х1	х2	х3	х4
Расстояние по модулю разности (c весами)	23,82	21,6752	19,543344	18,22024624

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

16. Рассчитываем сумму между составляющими векторов исследуемого предприятия и каждого эталонного образа:

(s+xi)
0,75	0,24	0,77	0,80
1,20	0,85	0,74	1,34
0,56	0,08	0,64	0,66
2,42	0,09	2,50	2,50
1,85	0,14	2,01	1,97

17. Рассчитываем модуль отношения (s-x_i)/(s+x_i) для каждой составляющей векторов исследуемого предприятия и каждого эталонного образа:

|(s-xi)/(s+xi)|
0,52	1,375	0,246753	0,125
0,183333	0,423529	0,635135	0,902985
0,892857	5,625	0,609375	0,484848
0,983471	25,66667	0,912	0,884
0,945946	11,85714	0,766169	0,756345

18. Таким образом, расстояния по Камберру (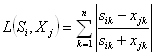) между исследуемым предприятием и эталонными образами будут равны:

	х1	х2	х3	х4
Расстояние по Камберру	3,525607	44,94734	3,169433	3,153179

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

ВЫВОД: В результате проведенного анализа можно сделать вывод о том, что уровень финансовой устойчивости исследуемого предприятия характеризуется относительной стабильностью и благополучием.

Задание 2

1. Задаем эталонные объекты, исследуемый образ и признаки, по которым будем оценивать сходство:

	Вектор признаков	в него можно класть вещи	сделано преимущественно из одного материала	имеет дверцу	в него можно увидеть свое отражение	на нем сидят
окно	X1	да	да	нет	да	нет
шкаф	X2	да	да	да	нет	нет
стул	X3	да	да	нет	нет	да
диван	X4	да	нет	нет	нет	да
стол *	S	да	да	да	нет	нет

* Цветом выделен исследуемый образ.

2. Переводим качественные характеристики объектов в количественные. В результате формируется двоичный массив:

	Вектор признаков	в него можно класть вещи	сделано преимущественно из одного материала	имеет дверцу	в него можно увидеть свое отражение	на нем сидят
окно	X1	1	1	0	1	0
шкаф	X2	1	1	1	0	0
стул	X3	1	1	0	0	1
диван	X4	1	0	0	0	1
стол *	S	1	1	1	0	0

3. Рассчитываем число совпадений наличия признаков объектов X_j, и S. Она может быть вычислена с помощью соотношения  (n – количество признаков). Для этого используем функцию СУММПРОИЗВ, указывая в ней массивы векторов значений признаков исследуемого образа и каждого из эталонного образов.

Таким образом:

		A (количество совпадений присутствия признаков у исследуемого объекта и эталона Xj)
окно	X1	2
шкаф	X2	3
стул	X3	2
диван	X4	1

4. С помощью переменной b подсчитывается число случаев, когда объекты X_j, и S _. не обладают одним и тем же признаком, . Для упрощения расчетов необходимо рассчитать матрицу значений (1-x_k) для всех исследуемых объектов:

		(1-xk)
окно	X1	0	0	1	0	1
шкаф	X2	0	0	0	1	1
стул	X3	0	0	1	1	0
диван	X4	0	1	1	1	0
стол *	X5	0	0	0	1	1

Рассчитываем значение переменной b аналогично методу расчета переменной a, используя значения матрицы, полученной в п.4:

		B (количество совпадений отсутствия признаков у исследуемого объекта и эталона Xj)
окно	X1	1
шкаф	X2	2
стул	X3	1
диван	X4	1