Навигация
Чисельне розв’язання задач оптимального керування
1 Дискретизація задачі із закріпленим лівим і вільним правим кінцем. Необхідні умови оптимальності
Розглянемо неперервну задачу оптимального керування
![]() ,(1)
,(1)
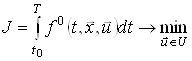 ,(2)
,(2)
![]() ,
, ![]() ,
, ![]() . (3)
. (3)
Виконаємо дискретну апроксимацію даної задачі. Для цього розіб’ємо відрізок ![]() точками
точками ![]() ,
, ![]() і будемо обчислювати значення цільового функціонала і закону руху тільки в точках розбиття:
і будемо обчислювати значення цільового функціонала і закону руху тільки в точках розбиття: ![]() ,
, ![]() ,
, ![]() . Закон руху в цьому випадку можна записати у вигляді:
. Закон руху в цьому випадку можна записати у вигляді:
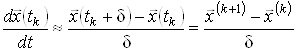 .
.
Тепер дискретна задача оптимального керування, що апроксимує неперервну задачу (1) – (3), матиме вигляд:
![]() ,
, ![]() , (4)
, (4)
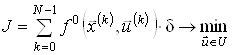 , (5)
, (5)
![]() (6)
(6)
![]() ,
, ![]() . (7)
. (7)
Для пошуку оптимального розв’язку отриманої дискретної задачі може бути застосований метод множників Лагранжа. Функція Лагранжа має вигляд:
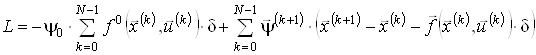 ,
,
![]() ,(8)
,(8)
де ![]() .
.
Обмеження на керування введемо далі, під час реалізації чисельного методу. Відзначимо, що перед першим доданком стоїть знак «–», оскільки ![]() і якщо не додавати «–», то характер екстремуму початкової функції зміниться.
і якщо не додавати «–», то характер екстремуму початкової функції зміниться.
Якщо ![]() – локально-оптимальний процес для задачі (4) – (7), то існують такі нерівні одночасно нулю множники Лагранжа
– локально-оптимальний процес для задачі (4) – (7), то існують такі нерівні одночасно нулю множники Лагранжа ![]() ,
, ![]() ,
, ![]() ,
, ![]() , що матимуть місце наступні умови:
, що матимуть місце наступні умови:
1. ![]() або
або
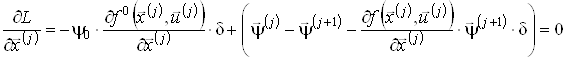 ,
,
![]() ,
,
![]() . (10)
. (10)
2. ![]() або
або
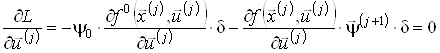 ,
,
![]() . (11)
. (11)
Із (9) одержимо ітераційні співвідношення для спряжених змінних ![]() , а з (10) – співвідношення для
, а з (10) – співвідношення для ![]() :
:
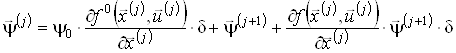
![]() , (12)
, (12)
![]() . (13)
. (13)
Перепишемо співвідношення (12) у вигляді:
 .
.
Очевидно, що останнє співвідношення є аналогом спряженої системи для неперервних задач керування. Дійсно,
 .
.
Якщо ![]() , то з останнього співвідношення одержимо
, то з останнього співвідношення одержимо
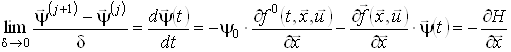 .
.
Зі співвідношення (13) випливає, що ![]() .
.
Сформулюємо критерій оптимальності для задачі (4) – (7). Вважатимемо, що функції ![]() ,
, ![]() неперервно-диференційовані за змінними
неперервно-диференційовані за змінними ![]() і опуклі за
і опуклі за ![]() . Тоді для локально-оптимального процесу
. Тоді для локально-оптимального процесу ![]() існують такі множники Лагранжа
існують такі множники Лагранжа ![]() ,
, ![]() ,
, ![]() ,
, ![]() , не всі рівні нулю одночасно, що матимуть місце необхідні умови екстремуму:
, не всі рівні нулю одночасно, що матимуть місце необхідні умови екстремуму:
1) умови стаціонарності в точці ![]() :
:
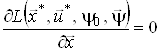 ;
;
2) ![]() . (14)
. (14)
Розпишемо (14), використовуючи вираз для функції Лагранжа:
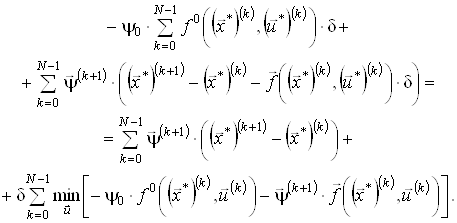
Перетворимо вираз під знаком мінімуму, переходячи до довільного ![]() :
:

Або

Якщо ![]() , то з останнього співвідношення одержимо
, то з останнього співвідношення одержимо
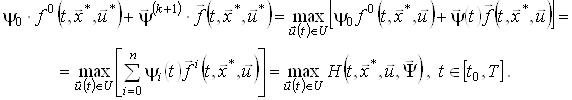
Розглянемо ітераційний метод пошуку оптимального керування задачі (4) – (7). Суть методу полягає в тому, що на кожній ітерації обчислюються два вектори: ![]() і
і ![]() . Перший із них містить
. Перший із них містить ![]() -е наближення для керувань у моменти часу
-е наближення для керувань у моменти часу ![]() для системи (14), при
для системи (14), при ![]() , а другий –
, а другий – ![]() -е наближення для фазових станів системи в ці ж моменти часу. Отже, на кожній ітерації ми одержуємо процес
-е наближення для фазових станів системи в ці ж моменти часу. Отже, на кожній ітерації ми одержуємо процес ![]() , що є
, що є ![]() -м наближенням до шуканого оптимального процесу.
-м наближенням до шуканого оптимального процесу.
Контроль у методі подвійного перерахування полягає в повторному перерахуванні результатів задачі і порівнянні отриманих даних для різних значень кроку розбиття. У випадку розбіжності виконується корекція і обчислення повторюються.
Розглянемо алгоритм методу.
1. Задаємо крок розбиття ![]() та точність обчислень
та точність обчислень ![]() .
.
2. Задаємо початкове наближення – припустимий набір керувань на кожному кроці – початкову стратегію керування:
![]() ,
, ![]() ,
, ![]() ,
,
де ![]() – наближення керування в момент
– наближення керування в момент ![]() на ітерації
на ітерації ![]() .
.
3. За визначеною в п. 2 стратегією керування ![]() будуємо фазову траєкторію процесу
будуємо фазову траєкторію процесу
![]() ,
, ![]() ,
, ![]()
на початкової ітерації ![]() , використовуючи початкові умови і різницеві співвідношення, що апроксимують рівняння руху:
, використовуючи початкові умови і різницеві співвідношення, що апроксимують рівняння руху:
![]()
![]() ,
, ![]() .
.
4. Визначаємо початкове наближення ![]() відповідно до (5).
відповідно до (5).
Похожие работы
... провести, то одержимо співвідношення . Це означає, що різним реалізаціям випадкового збурення для одного початкового стану відповідатимуть різні оптимальні стратегії керування . 4 Формальна постановка задачі оптимального стохастичного керування Розглянемо систему (2) із цільовим функціоналом (3). Надалі, якщо інше не обговорено спеціально, будемо вважати, що оптимальні керування на ...
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
... у формулу (2.11) і визначити наступний стан системи . Для зміненого стану знайти оптимальне управління , підставити у формулу (2.11) і так далі. Для і-гo стану , знайти і і т.д. [1]. 3. Оптимальний розподіл інвестицій, як задача динамічного програмування Інвестор виділяє кошти в розмірі умовних одиниць, котрі повинні бути розподілені між -підприємствами. Кожне і-те підприємство при і ...
... груп за визначений період часу. За допомогою цих даних (статистичної вибірки) ми зможемо описати закон розподілу попиту, на основі якого в подальшому буде ґрунтуватись оптимальне використання складських приміщень. Масштабування даних – переведення з одиниць виміру «пляшки» в «ящики» для зручності розрахунків. Обчислення середніх значень попиту на товари за період та окремо по кожному виду. ...





0 комментариев