Навигация
Знаходимо спряжені змінні за формулами (12) – (13)
5. Знаходимо спряжені змінні за формулами (12) – (13).
Визначаємо наступні наближення до оптимального керування ![]() ,
,
![]()
в момент ![]() як розв’язки задачі (15) або (16):
як розв’язки задачі (15) або (16):
![]() ,
, ![]() .
.
7. Обчислюємо відповідну стратегії ![]() траєкторію
траєкторію
![]()
за формулами (4), (6):
![]() ,
, ![]() ,
, ![]() .
.
8. Знаходимо наступне наближення цільового функціонала
![]() за формулою (5).
за формулою (5).
9. Якщо ![]() , то переходимо до п. 10, інакше вважаємо, що
, то переходимо до п. 10, інакше вважаємо, що
![]() ,
, ![]() ,
, ![]() і переходимо до п. 13.
і переходимо до п. 13.
10. Перевіряємо, чи виконується задана точність обчислень. Якщо
![]() і
і ![]() ,
,
то переходимо до п. 13, інакше – до п. 11.
11. Позначаємо
![]() ,
, ![]() ,
, ![]() .
.
12. Виконуємо наступний крок ітераційного методу – п. 5.
13. Позначаємо
![]() ,
, ![]() ,
, ![]() – розв’язок, отриманий із кроком розбиття
– розв’язок, отриманий із кроком розбиття ![]() .
.
1 Якщо крок ![]() не ділився, то переходимо до п. 15, інакше – до п. 1
не ділився, то переходимо до п. 15, інакше – до п. 1
15. Ділимо крок
![]() . Тоді
. Тоді ![]() і переходимо до п. 2 при
і переходимо до п. 2 при ![]() .
.
1 Перевіряємо задану точність. Якщо
![]() і
і ![]() ,
,
то переходимо до п. 18, інакше переходимо до п. 17.
17. Позначаємо
![]() ,
, ![]() ,
, ![]() ,
, ![]() , і переходимо до п. 15 – наступного кроку подвійного перерахування.
, і переходимо до п. 15 – наступного кроку подвійного перерахування.
18. ![]() ,
, ![]() ,
, ![]() – розв’язок задачі.
– розв’язок задачі.
Кінець алгоритму.
3. Оптимальне стохастичне керування: формулювання із зовнішнім інтеграломРозглянемо відображення ![]() , що задане формулою
, що задане формулою
![]() , (17)
, (17)
за таких припущень:
параметр ![]() приймає значення з вимірного простору
приймає значення з вимірного простору ![]() . Для будь-якої фіксованої пари
. Для будь-якої фіксованої пари ![]() задана ймовірнісна міра
задана ймовірнісна міра ![]() на просторі
на просторі ![]() , а символ
, а символ ![]() у формулі (12) означає зовнішній інтеграл відносно цієї міри. Отже,
у формулі (12) означає зовнішній інтеграл відносно цієї міри. Отже,
![]() ;
;
функції ![]() і
і ![]() відображують множину
відображують множину ![]() відповідно в множини
відповідно в множини ![]() і
і ![]() , тобто
, тобто ![]() ,
, ![]() ;
;
скаляр ![]() додатний.
додатний.
Формули (1), (6) є окремими випадками відображення ![]() з (12). Очевидно, що відображення (1) для детермінованої задачі випливає з (12), якщо множина
з (12). Очевидно, що відображення (1) для детермінованої задачі випливає з (12), якщо множина ![]() складається з єдиного елемента, а відображення (6) (для стохастичної задачі зі зліченним простором збурень) відповідає випадку, коли множина
складається з єдиного елемента, а відображення (6) (для стохастичної задачі зі зліченним простором збурень) відповідає випадку, коли множина ![]() зліченна, а
зліченна, а ![]() є
є ![]() -алгеброю, складеною із всіх підмножин
-алгеброю, складеною із всіх підмножин ![]() .
.
Очевидно, що відображення ![]() з (12) задовольняє припущенню монотонності. Якщо на множини
з (12) задовольняє припущенню монотонності. Якщо на множини ![]() ,
, ![]() і функції
і функції ![]() ,
, ![]() і
і ![]() накласти вимоги вимірності, то витрати за
накласти вимоги вимірності, то витрати за ![]() кроків
кроків ![]() можна визначити в термінах звичайного інтегрування для будь-якої стратегії
можна визначити в термінах звичайного інтегрування для будь-якої стратегії ![]() , для якої функції
, для якої функції ![]() ,
, ![]() вимірні.
вимірні.
Для початкового стану ![]() і стратегії
і стратегії ![]() ймовірнісні міри
ймовірнісні міри
![]() , ...,
, ..., ![]()
у сукупності із системою рівнянь
![]() ,
, ![]() (18)
(18)
визначають єдину міру ![]() на
на ![]() -кратному прямому добутку
-кратному прямому добутку ![]() копій простору
копій простору ![]() . У випадку, якщо
. У випадку, якщо ![]() ,
, ![]() , і виконується одна з умов
, і виконується одна з умов
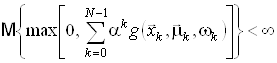 або
або
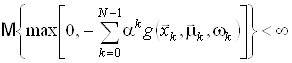 ,
,
то функція витрат за ![]() кроків, що відповідає вимірній стратегії
кроків, що відповідає вимірній стратегії ![]() , приводиться до звичайного вигляду
, приводиться до звичайного вигляду![]() ,
,
де стани ![]() ,
, ![]() виражено як функції змінних
виражено як функції змінних ![]() , ...,
, ..., ![]() за допомогою рівнянь (13) та початкового стану
за допомогою рівнянь (13) та початкового стану ![]() .
.
Рекурентне співвідношення методу динамічного програмування для розв’язання багатоетапних задач оптимального стохастичного керування зі скінченним горизонтом можна записати так:
![]() ,
, ![]() ,
,
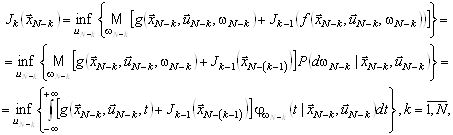
де ![]() – щільність розподілу величини
– щільність розподілу величини ![]() .
.
Розглянемо відображення ![]() , що задане формулою
, що задане формулою
![]() , (19)
, (19)
за припущення, що параметр ![]() приймає значення зі зліченної множини
приймає значення зі зліченної множини ![]() відповідно до заданого розподілу ймовірностей, що залежать від стану
відповідно до заданого розподілу ймовірностей, що залежать від стану ![]() і керування
і керування ![]() . Вважатимемо також, що
. Вважатимемо також, що ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тоді відображення
. Тоді відображення ![]() з формули (14) задовольняє припущенню монотонності.
з формули (14) задовольняє припущенню монотонності.
Якщо ![]() ,
, ![]() , то задача оптимального керування з мультиплікативним функціоналом витрат і скінченним горизонтом
, то задача оптимального керування з мультиплікативним функціоналом витрат і скінченним горизонтом ![]() матиме такий вигляд:
матиме такий вигляд:
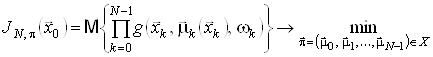 , (20)
, (20)
![]() . (21)
. (21)
а відповідна задача з нескінченним горизонтом:
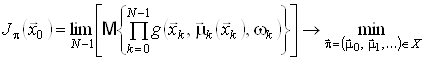 , (22)
, (22)
![]() . (23)
. (23)
Границя в (23) існує, якщо ![]() :
: ![]() або
або ![]() .
.
Самостійний інтерес становить задача з експоненціальною функцією витрат
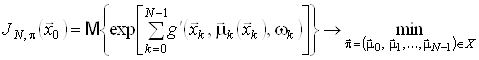 ,
,
![]() ,
,
де ![]() .
.
Для розв’язання багатоетапних задач оптимального стохастичного керування з мультиплікативним функціоналом витрат використовується таке рекурентне співвідношення алгоритму динамічного програмування:
![]() ,
, ![]() ,
,
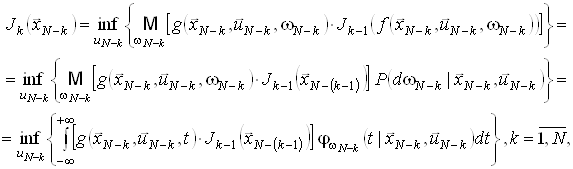
де ![]() – щільність розподілу величини
– щільність розподілу величини ![]() .
.
Розглянемо задачу керування системою, у якій некерованими впливами є стратегії супротивника (або явища природи) ![]() ,
, ![]() , що обираються залежно від поточного стану
, що обираються залежно від поточного стану ![]() і керування
і керування ![]() . Вважатимемо, що припустимі стратегії супротивника приймають значення із множини
. Вважатимемо, що припустимі стратегії супротивника приймають значення із множини ![]() ,
, ![]() . Будемо обчислювати стратегію керування
. Будемо обчислювати стратегію керування ![]() , орієнтуючись на найгіршу поведінку супротивника. Розглянемо відображення
, орієнтуючись на найгіршу поведінку супротивника. Розглянемо відображення ![]() , задане формулою
, задане формулою
![]() ,
,
за таких припущень:
параметр ![]() приймає значення з деякої множини
приймає значення з деякої множини ![]() , а
, а ![]() – непуста підмножина
– непуста підмножина ![]() при будь-яких
при будь-яких ![]() ,
, ![]() ;
;
функції ![]() і
і ![]() відображують множину
відображують множину ![]() в множини
в множини ![]() та
та ![]() відповідно, тобто
відповідно, тобто ![]() ,
, ![]() ;
;
скаляр ![]() додатний.
додатний.
За таких умов припущення про монотонність для відображення ![]() має місце. Якщо при цьому
має місце. Якщо при цьому ![]() ,
, ![]() і
і ![]() для всіх
для всіх ![]() ,
, ![]() ,
, ![]() , то відповідну
, то відповідну ![]() -крокову задачу мінімаксного керування можна сформулювати так:
-крокову задачу мінімаксного керування можна сформулювати так:
 , (17)
, (17)
![]() . (18)
. (18)
Задача з нескінченним горизонтом формулюється аналогічно:
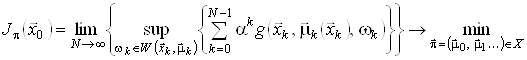 , (24)
, (24)
![]() . (25)
. (25)
Границя у співвідношенні (25) існує при виконанні будь-якої з умов:
· ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
· ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
· ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() і деякого
і деякого ![]() .
.
Для розв’язання багатокрокових мінімаксних задач оптимального стохастичного керування рекурентне співвідношення алгоритму динамічного програмування використовується у такому вигляді:
![]() ,
, ![]() ,
,
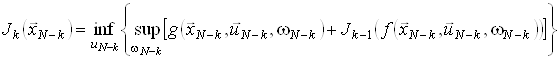 ,
,
![]() .
.
Похожие работы
... провести, то одержимо співвідношення . Це означає, що різним реалізаціям випадкового збурення для одного початкового стану відповідатимуть різні оптимальні стратегії керування . 4 Формальна постановка задачі оптимального стохастичного керування Розглянемо систему (2) із цільовим функціоналом (3). Надалі, якщо інше не обговорено спеціально, будемо вважати, що оптимальні керування на ...
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
... у формулу (2.11) і визначити наступний стан системи . Для зміненого стану знайти оптимальне управління , підставити у формулу (2.11) і так далі. Для і-гo стану , знайти і і т.д. [1]. 3. Оптимальний розподіл інвестицій, як задача динамічного програмування Інвестор виділяє кошти в розмірі умовних одиниць, котрі повинні бути розподілені між -підприємствами. Кожне і-те підприємство при і ...
... груп за визначений період часу. За допомогою цих даних (статистичної вибірки) ми зможемо описати закон розподілу попиту, на основі якого в подальшому буде ґрунтуватись оптимальне використання складських приміщень. Масштабування даних – переведення з одиниць виміру «пляшки» в «ящики» для зручності розрахунків. Обчислення середніх значень попиту на товари за період та окремо по кожному виду. ...





0 комментариев