Навигация
Статические характеристики САУ переменного тока
2. Статические характеристики САУ переменного тока
2.1 Математическое описание преобразователя частоты (ПЧ) с промежуточным звеном постоянного тока на основе АИН
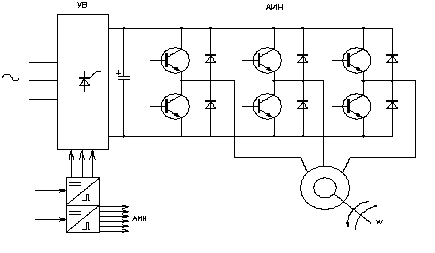
УВ – управляемый выпрямитель, отвечает за напряжение подаваемое на асинхронный двигатель;
АИН – автономный инвертор напряжения, отвечает за частоту подаваемого напряжения на асинхронный двигатель.
Функциональная схема преобразователя частоты
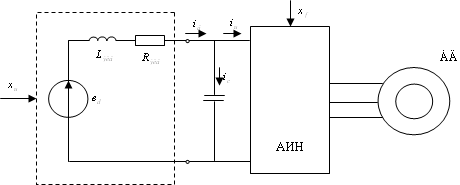
Исходное дифференциальное уравнение
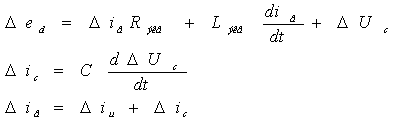
Запишем эти уравнения в операторной форме
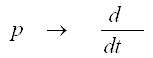
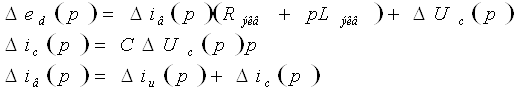
Структурная схема ПЧ на основе АИН.
2.2 Математическое описание асинхронного двигателя при управлении частотой и напряжением статора
При исследовании переходных процессов в трехфазных асинхронных электродвигателях целесообразно принять следующие допущения, позволяющие в доступной математической форме выразить соотношения основных параметров и координат электродвигателя:
1) намагничивающие силы обмоток двигателя распределены синусоидально вдоль окружности воздушного зазора;
2) потери встали статора и ротора отсутствуют;
3) обмотки статора и ротора строго симметричны со сдвигом осей обмоток на 120°;
4) насыщение магнитной цепи отсутствует.
Уравнения равновесия напряжений для обмоток трех фаз статора имеют вид
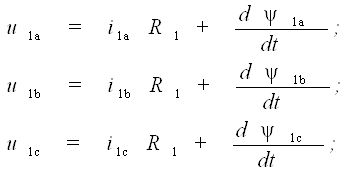 (1)
(1)
Соответственно для обмоток трех фаз ротора
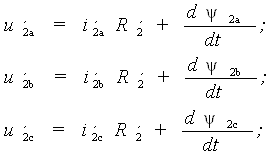 (2)
(2)
Где ![]() — мгновенные значения фазных напряжений статора и ротора;
— мгновенные значения фазных напряжений статора и ротора;
![]() — мгновенные значения фазных токов статора и ротора;
— мгновенные значения фазных токов статора и ротора;
![]() - полные потокосцепления фазных обмоток;
- полные потокосцепления фазных обмоток;
R1, R2 — активные сопротивления обмоток статора и ротора.
Асинхронный электродвигатель представляет собой систему магнитно-связанных обмоток, расположенных на статоре и роторе. При вращении ротора взаимное положение обмоток статора и ротора непрерывно изменяется, соответственно изменяется и взаимная индуктивность между ними. С учетом принятых допущений можно считать, что взаимная индуктивность пропорциональна косинусу текущего угла между осями обмоток ротора и статора.
При математическом описании трехфазных асинхронных двигателей удобно оперировать не мгновенным значениями координат, а их результирующими векторами. Если, например, мгновенные значения токов равны ia, ib, ic, то результирующий вектор тока определяется уравнением:
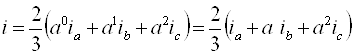 ,
,
Где a0=ej0=1; a=ej2π/3; a2= ej4π/3.
Аналогично определяются результирующие векторы напряжения
![]()
и потокосцепления
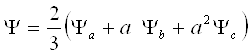
Используя выражения результирующих векторов, уравнения (1) можно записать в виде одного дифференциального уравнения в векторной форме. Для этого первое уравнение из (1) умножается на 2/3a0, второе на 2/3a, третье на 2/3a2. Суммируя полученные произведения, получим
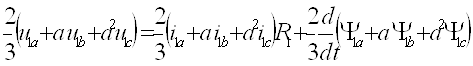
или в векторной форме
![]() (4)
(4)
Аналогично векторное уравнение напряжений ротора:
![]() (5)
(5)
В уравнениях (4) и (5) векторы записаны соответственно в системах координат статора и ротора. Для совместного решения уравнений их необходимо привести к одной системе координат.
При исследовании переходных процессов в электродвигателях переменного тока применяют различные ортогональные системы координат, отличающиеся угловой скоростью вращения координатных осей сок, например системы, оси которых неподвижны относительно ротора, или неподвижны относительно статора, или вращаются с синхронной скоростью.
Уравнения асинхронного электродвигателя в системе координат, вращающейся с произвольной скоростью ωк, имеют вид
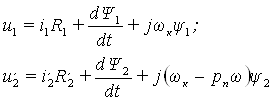 (6)
(6)
где ω — угловая скорость вращения ротора; pп — число пар полюсов.
При исследовании переходных процессов в асинхронном электродвигателе, управляемом частотой и напряжением статора, удобно использовать систему координат, вращающуюся со скоростью ωк, равной угловой скорости вращения магнитного поля ω0’, приведенной к числу пар полюсов, равному единице (приведенной к двухполюсному электродвигателю). Предполагается при этом справедливым равенство
![]() ,
,
где f1 — частота напряжения статора, Гц; ω1 — угловая частота напряжения статора, рад/с.
На основании уравнений (6) для рассматриваемой координатной системы можно записать
 (7)
(7)
где s — скольжение электродвигателя:
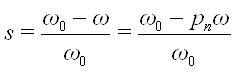
(ω0= ω0’/pп — угловая скорость вращения магнитного поля, или синхронная скорость электродвигателя).
Потокосцепления связаны с токами через индуктивности
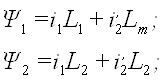 (8)
(8)
Для определения электромагнитного момента асинхронного электродвигателя используется векторное произведение ψ1 и i1
тогда
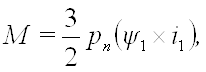 (9)
(9)
или векторное произведение ψ2 и i2’, тогда
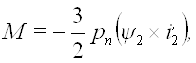 (10)
(10)
Учитывая выражения (8), можно записать (9) и (10) в виде
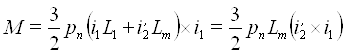 ; (11)
; (11)
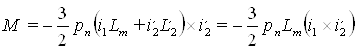 . (12)
. (12)
Вторые равенства в уравнениях (11), (12) справедливы потому, что векторное произведение двух одинаково направленных векторов равно нулю.
Для полного описания переходных процессов в асинхронном электродвигателе к уравнениям напряжений и моментов следуй добавить уравнение
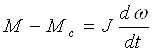 ,
(13)
,
(13)
записанное для скалярных значений моментов М и Мс.
Полученная система уравнений электродвигателя является нелинейной, и решение ее для различных динамических режимов работы электродвигателя может быть выполнено с использованием вычислительных машин. При синтезе систем управления асинхронным электродвигателем целесообразно располагать простыми и наглядными динамическими моделями электродвигателя в виде передаточных функций или структурных схем. Такая возможность появляется, если рассматривать переходные процессы в отклонениях относительно начальных координат электродвигателя.
Сравнительно простая структурная схема может быть получена, если пренебречь активным сопротивлением статорной цепи, т. е. положить R1=0. Безусловно, что такое пренебрежение накладывает определенные ограничения на использование получаемых моделей. Они вполне применимы для систем с небольшим диапазоном регулирования скорости относительно синхронной скорости, для электродвигателей средней и большой мощности. При широком регулировании скорости, а также для электродвигателей малой мощности необходимы уточнения структурных схем.
Для дальнейших исследований динамических свойств асинхронных ^ электродвигателей целесообразно результирующие векторы представить в виде проекций на комплексной плоскости и записать их через вещественные и мнимые части в следующем виде:
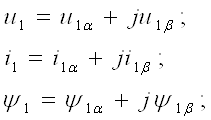
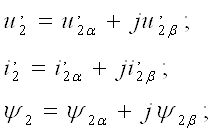 (14)
(14)
Совместив вектор напряжения статора с действительной осью координатной системы, т. е. положив u1β=0, на основании (7) получим
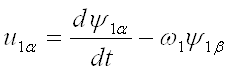 ; (15)
; (15)
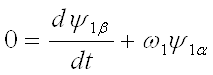 ; (16)
; (16)
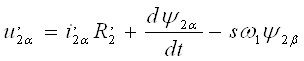 ; (17)
; (17)
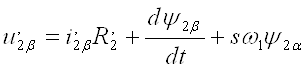 . (18)
. (18)
Выразив также электромагнитный момент по уравнению (9) через составляющие векторов тока и потокосцепления
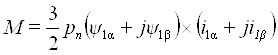
и применив правило векторного произведения векторов, получим абсолютное значение момента:
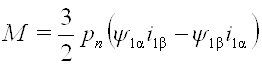 , (19a)
, (19a)
где ![]() ;
;
![]()
Воспользовавшись выражением (10), можно аналогично получить
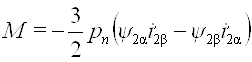 (19б)
(19б)
где ![]() ;
;
![]()
Составляющие тока ротора могут быть выражены через составляющие потокосцепления в следующем виде:
 (20)
(20)
где k1 - коэффициент электромагнитной связи статора;
k1=Lm/L1; (21a)
![]() . (21б)
. (21б)
С учетом (8) и (21а) можно выражения моментов записать в форме, удобной для вывода передаточных функций двигателя;
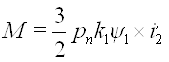
или
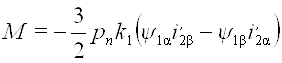 . (22)
. (22)
В случае одновременного изменения частоты и напряжения статора, при котором потокосцепление статора остается постоянным, из уравнений (15) и (16) можно получить
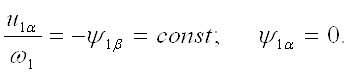 (23)
(23)
Для двигателя с короткозамкнутым ротором в уравнениях (17), (18) ![]() . Выразив из уравнений (20) ψ2α и ψ2β и подставив их в уравнения (17), (18), получим
. Выразив из уравнений (20) ψ2α и ψ2β и подставив их в уравнения (17), (18), получим
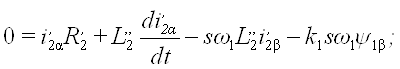 (24)
(24)
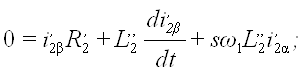 (25)
(25)
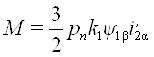 . (26)
. (26)
Рассматривая переменные величины в приращениях относительно начальных значений ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , получим из (23) - (26) уравнения для статического режима, связывающие начальные значения координат,
, получим из (23) - (26) уравнения для статического режима, связывающие начальные значения координат,
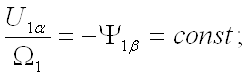 (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
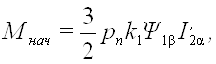 (30)
(30)
и уравнения для динамического режима, связывающие приращения координат:
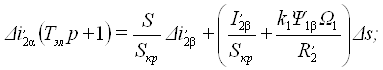 (31)
(31)
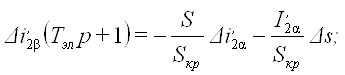 (32)
(32)
 (33)
(33)
где ![]() - электромагнитная постоянная времени электродвигателя;
- электромагнитная постоянная времени электродвигателя;
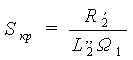 - критическое скольжение.
- критическое скольжение.
На основании уравнений (27)-(33) можно записать передаточную функцию
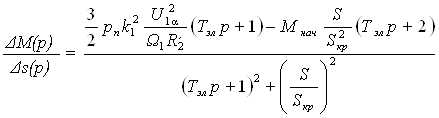 (34)
(34)
Выражение 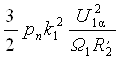 в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф. определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора U1α и угловой частоты напряжения статора Ω1:
в первом слагаемом числителя (34) представляет собой значение фиктивного пускового момента Мп.ф. определяемое в результате линеаризации рабочей части механической характеристики двигателя для принятых значений напряжения статора U1α и угловой частоты напряжения статора Ω1:
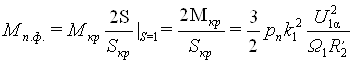 , (35)
, (35)
где 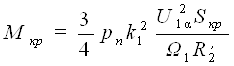 - критический момент двигателя.
- критический момент двигателя.
Момент Мнач во втором слагаемом числителя (34) можно записать с учетом принятых допущений в виде
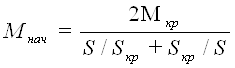 , (36)
, (36)
С учетом (35) и (36) выражение (34) примет следующий вид:
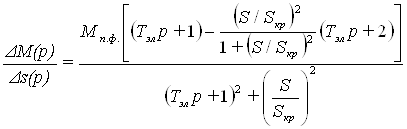 . (37)
. (37)
Для рабочей части механической характеристики двигателя можно принять
![]() ,
,
и тогда передаточную функцию (37) можно записать в упрощенном виде
 (38)
(38)
Представив зависимость скольжения электродвигателя от угловой частоты напряжения статора в приращениях и выполнив линеаризацию при условии, что в рабочей области s<<l, получим
 (39)
(39)
Уравнение равновесия моментов (13) может быть записано в приращениях в виде
![]() . (40)
. (40)
На основании полученных выражений может быть составлена структурная схема асинхронного двигателя при управлении угловой частотой напряжения статора и при условии постоянства потокосцепления статора. Однако это удобнее сделать, если представить координаты двигателя в о. е., приняв за базовые значения координат их значения в номинальном режиме: Мп.ф.н., Ω1н, U1αн, Ω0н=Ω1н/pп где Ω0н - синхронная угловая скорость двигателя. Тогда ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Передаточная функция (37) с учетом (39) запишется так:
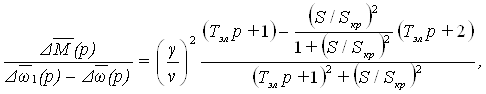 (41)
(41)
где γ=U1α/U1αн - относительное напряжение статора; ν=Ω1/Ω1н – относительная частота напряжения статора.
Или в упрощенном виде:
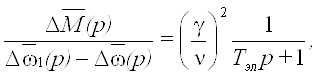 (42)
(42)
Соответственно на основании уравнения (40) имеем
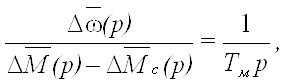 (43)
(43)
где Tм=JΩ0н/Мп.ф.н - механическая постоянная времени двигателя.
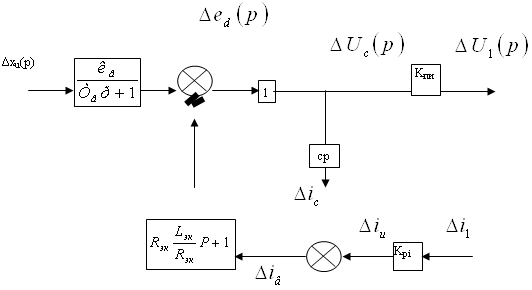
Упрощенная структурная схема асинхронного двигателя при управлении угловой частотой напряжения статора, построенная на основании выражений (42), (43), показана на рис. 1.
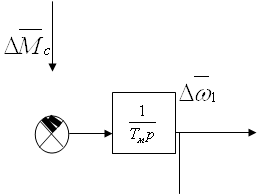 | |||
 | |||
![]()
![]()
![]()
![]()
Рис.1.
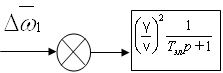
Используя изложенный выше подход к выводу передаточных функций двигателя, можно получить передаточную функцию, связывающую изменение электромагнитного момента двигателя ΔМ при изменении напряжения статора Δu1α и неизменной частоте напряжения статора (ω1=const). Этот случай соответствует изменяющемуся потокосцеплению статора. В о. е. получим
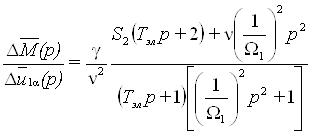 , (44)
, (44)
Где S2 - абсолютное скольжение электродвигателя в рабочей точке, равное отношению угловой частоты ЭДС ротора Ω2 (приведенной к двухполюсному электродвигателю) к номинальному значению угловой частоты напряжения статора Ω1н.
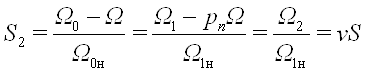 .
.
Структурная схема асинхронного электродвигателя при управлении напряжением статора показана на рис. 2.

Рис.2.
Похожие работы
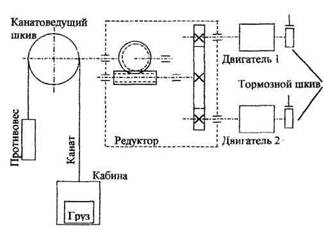
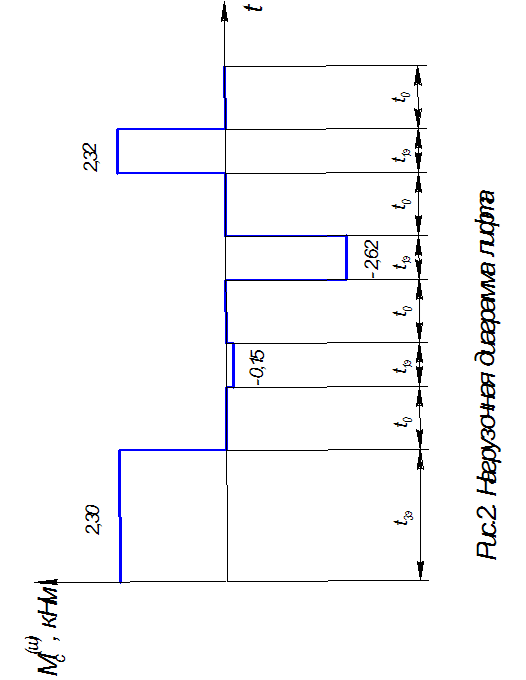
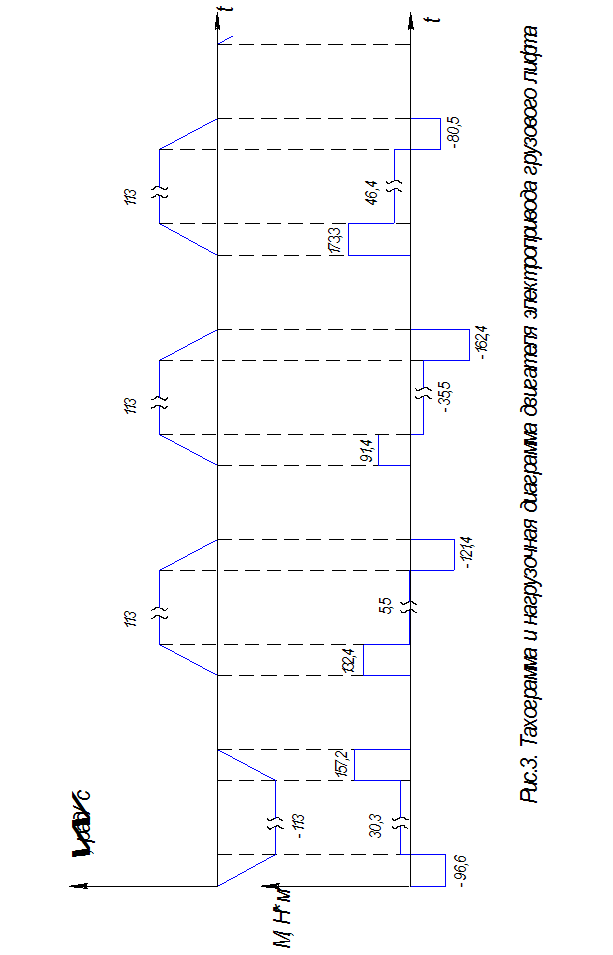
... числа редуктора Расчет передаточного числа редуктора выполняется так, чтобы максимальной скорости рабочего органа механизма соответствовала номинальная скорость двигателя. Для привода грузового лифта: Расчет и построение нагрузочной диаграммы двигателя Для проверки предварительно выбранного двигателя по нагреву выполним построение упрощенной нагрузочной диаграммы двигателя (т.е. ...
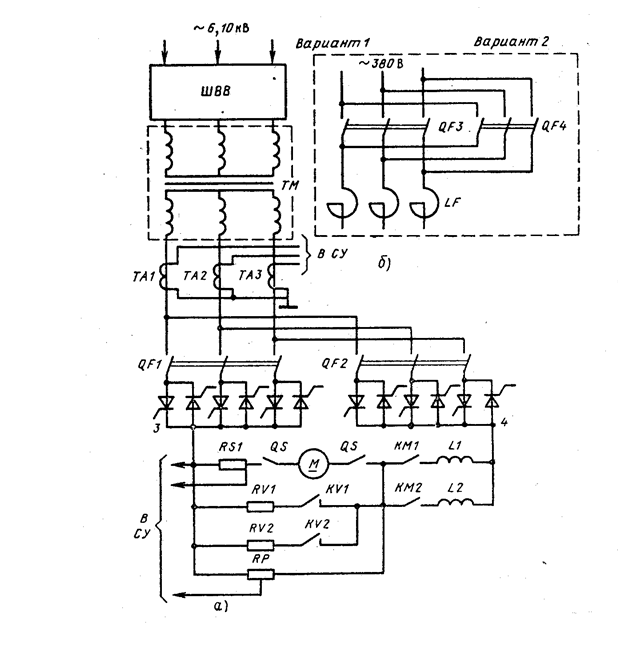
... силовой преобразовательный агрегат, силовой трансформатор и реакторы, выполнить расчет элементов системы автоматического управления электроприводом, выполнить компьютерное моделирование системы автоматизированного электропривода в типовых режимах. Требования к электроприводу: 1. Обеспечение работы механизма по следующему циклу: • подход детали к резцу с пониженной скоростью; • ...
... о выборе лучшего варианта привода принимается на основе сопоставления приведенных затрат на одинаковый объем выпускаемой продукции. В данном проекте необходимо обеспечить регулирование продолжительности времени выпечки с коррекцией по температуре во второй зоне пекарной камеры. При этом необходимо учитывать, что производительность печи при замене системы привода меняться не должна, а также ...
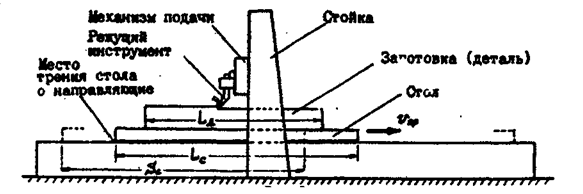
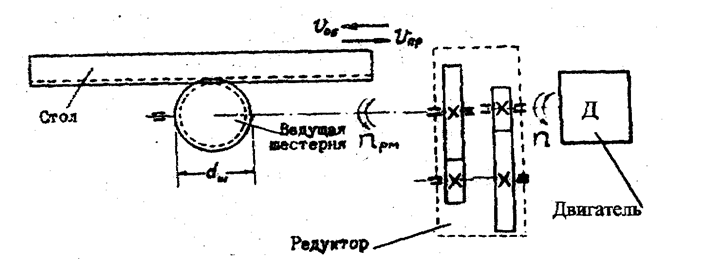
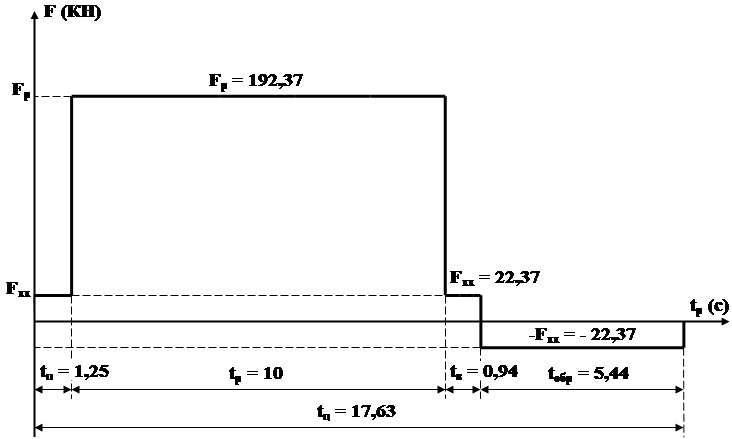
... , пройденный столом на интервале 11: Продолжительность интервала 11: Момент двигателя на интервале 5: Рисунок 4 Тахограмма и нагрузочная диаграмма электропривода механизма перемещения стола продольно-строгального станка. Нагрузочная диаграмма и тахограмма двигателя представлены на рисунке 4: 3.4 Проверка двигателя по нагреву Для проверки двигателя по ...
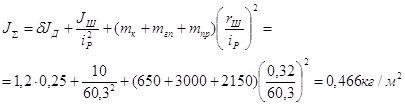

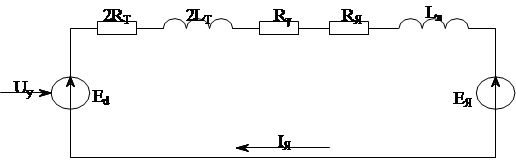



0 комментариев