Навигация
СТАТИСТИЧЕСКИЕ МЕТОДЫ ВЫЯВЛЕНИЯ СЕЗОННЫХ КОЛЕБАНИЙ
2. СТАТИСТИЧЕСКИЕ МЕТОДЫ ВЫЯВЛЕНИЯ СЕЗОННЫХ КОЛЕБАНИЙ
В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности iS. Совокупность этих показателей отражает сезонную волну.
В общем виде они определяются отношением исходных (эмпирических) уровней ряда динамики ![]() к теоретическим (расчетным) уровням
к теоретическим (расчетным) уровням ![]() , выступающим в качестве базы сравнения:
, выступающим в качестве базы сравнения:
![]() .
(2.1)
.
(2.1)
Именно в результате того, что в этой формуле измерение сезонных колебаний производится на базе соответствующих теоретических уровней тренда ![]() , в исчисляемых при этом индивидуальных индексах сезонности влияние основной тенденции развития элиминируется (устраняется).
, в исчисляемых при этом индивидуальных индексах сезонности влияние основной тенденции развития элиминируется (устраняется).
Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам.
Поскольку на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются обобщенные показатели в виде средних индексов сезонности ![]() :
:
![]() .
(2.2)
.
(2.2)
Вычисленные на основе этой формулы средние индексы сезонности (с применением в качестве базы сравнения соответствующих уровней тренда) свободны от влияния основной тенденции развития и случайных отклонений.
В зависимости от характера тренда формула (2.2) принимает следующие формы:
1) для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития
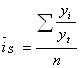 . (2.3)
. (2.3)
Выступающие при этом в качестве переменной базы сравнения теоретические уровни ![]() представляют своего рода "среднюю ось кривой", так как их расчет основан на положениях метода наименьших квадратов. Поэтому измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней;
представляют своего рода "среднюю ось кривой", так как их расчет основан на положениях метода наименьших квадратов. Поэтому измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней;
2) для рядов внутригодовой динамики, в которых повышающийся (снижающийся) тренд отсутствует или он незначителен
 .
(2.4)
.
(2.4)
В формуле (2.4) базой сравнения является общий для анализируемого ряда динамики средний уровень ![]() . Поскольку для всех эмпирических уровней анализируемого ряда динамики этот общий средний уровень является постоянной величиной, то применение формулы (2.4) называется способом постоянной средней.
. Поскольку для всех эмпирических уровней анализируемого ряда динамики этот общий средний уровень является постоянной величиной, то применение формулы (2.4) называется способом постоянной средней.
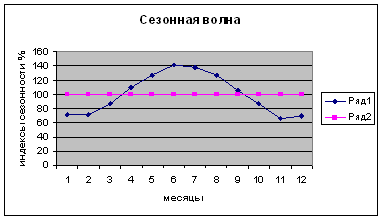
Для наглядного представления сезонной волны исчисленные индексы сезонности изображают в виде графика (линейной диаграммы).
Для определения в формуле (2.1) теоретических уровней тренда ![]() важно правильно подобрать математическую функцию, по которой будет производиться аналитическое выравнивание в анализируемом ряду динамики. Это наиболее сложный и ответственный этап изучения сезонных колебаний. От обоснованности подбора той или иной математической функции во многом зависит практическая значимость получаемых в анализе индексов сезонности.
важно правильно подобрать математическую функцию, по которой будет производиться аналитическое выравнивание в анализируемом ряду динамики. Это наиболее сложный и ответственный этап изучения сезонных колебаний. От обоснованности подбора той или иной математической функции во многом зависит практическая значимость получаемых в анализе индексов сезонности.
При использовании способа аналитического выравнивания ход вычислений индексов сезонности следующий:
- по соответствующему полиному вычисляются для каждого месяца (квартала) выравненные уровни на момент времени t;
- определяются отношения фактических месячных (квартальных) данных к соответствующим выравненным данным (в процентах);
- находятся средний арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах.
Расчет заканчивается проверкой правильности вычислений индексов. Так как средний индекс сезонности для всех месяцев (кварталов) должен быть 100%, то сумма полученных индексов по месячным данным равна 1200, а сумма по четырем кварталам – 400.
Классификация наиболее распространенных методов измерения сезонных волн представлена в таблице 2.1.
Таблица 2.1
Классификация методов измерения сезонных волн
| Методы измерения сезонных волн, основанные на применении | Наименование методов вычисления сезонных волн |
| I. Средней арифметической | 1. Метод абсолютных разностей 2. Метод отношений средних помесячных к средней за весь период 3. Метод отношений помесячных уровней к средней данного года |
| II. Относительных величин | 1. Метод относительных величин 2. Метод относительных величин на основе медианы 3. Метод У. Персона (цепной метод) |
| III. Механического выравнивания | 1. Метод скользящих средних 2. Метод скользящих сумм и скользящих средних |
| IV. Аналитического выравнивания | 1. Выравнивание по прямой 2. Выравнивание по параболе и экспоненте 3. Выравнивание по ряду Фурье |
3. ИЗУЧЕНИЕ СЕЗОННЫХ КОЛЕБАНИЙ В ДЕЯТЕЛЬНОСТИ ТОРГОВОГО ПРЕДПРИЯТИЯ
Применение формул для изучения сезонных колебаний проиллюстрируем на примере одного из торговых предприятий.
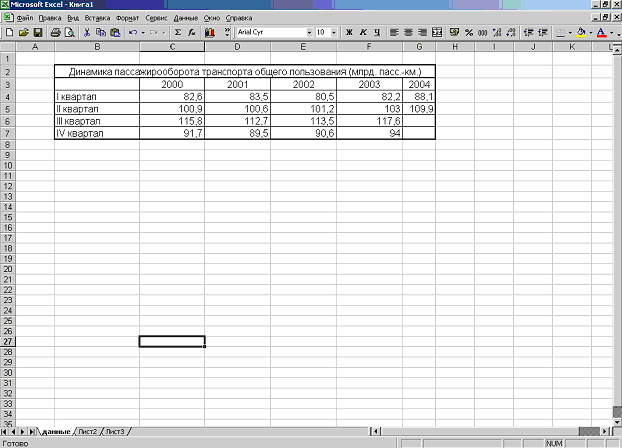
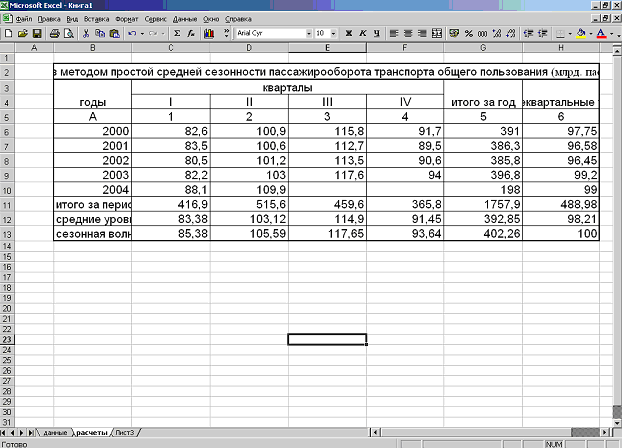
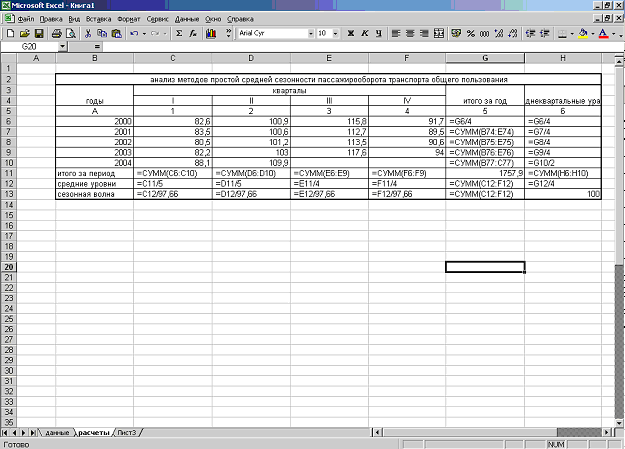
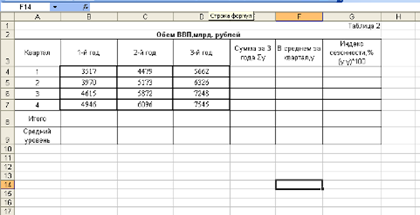
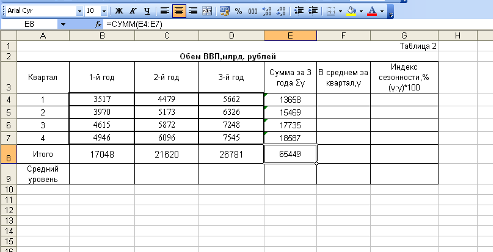
Имеются данные о продаже молочных продуктов в одном из магазинов г. Тюмени по кварталам 2000 – 2003 гг.
Таблица 3.1
Среднедневная реализация, т
| Квартал | 2000 | 2001 | 2002 | 2003 |
| 1 | 2 | 3 | 4 | 5 |
| I II III IV | 49,9 75,8 73,9 48,5 | 48,1 92,3 93,4 55,1 | 50,9 106,5 108,8 68,8 | 60,7 120,6 126,7 70,5 |
| Годовая | 62,0 | 72,2 | 83,8 | 94,6 |
| Темпы роста, в % к 2000 г. в % по годам Абсолютный прирост по годам, m Темп наращивания, % | 100,0 - - - | 116,5 116,5 10,2 16,5 | 135,2 116,1 11,6 18,7 | 152,6 112,9 10,8 17,4 |
Необходимо вычислить индексы сезонных колебаний реализации данных продуктов.
Из таблицы 3.1 видно, что в 2003 г. рост продажи молочных продуктов по сравнению с 2000 г. достиг 152,6%, или в среднем за год интенсивность роста составила 115,1% ![]() . Это позволяет считать, что в анализируемом году динамики имеется значительная тенденция роста.
. Это позволяет считать, что в анализируемом году динамики имеется значительная тенденция роста.
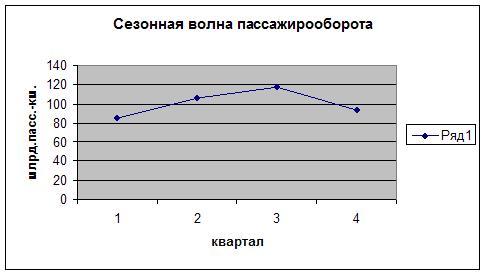
Графическое изображение исходной информации подтверждает эти выводы (рис. 3.1).
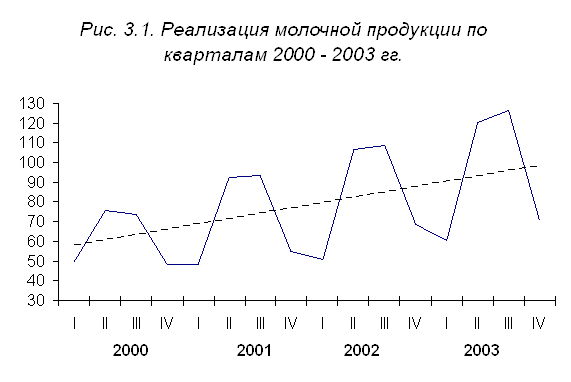
Выводы о значительном росте реализации данной продукции в 2000 – 2003гг. предопределяет выбор формулы (2.1) для расчета индексов сезонности способом переменной средней.
По содержащимся в таблице 3.1 показателям анализируемого ряда динамики можно выдвинуть рабочую гипотезу о возможных типах математических функций для получения теоретических уровней тренда.
С известной степенью приближения это может быть прямолинейная функция:
![]() (3.1)
(3.1)
В основе такого предположения лежит характер изменения абсолютных приростов. При общем среднем абсолютном приросте 10,9m ![]() отклонения по отдельным годам не столь значительны: -0,7m в 2001 г. и +0,7m в 2002 г.
отклонения по отдельным годам не столь значительны: -0,7m в 2001 г. и +0,7m в 2002 г.
Но при наибольшем абсолютном приросте в 2002 г. (+11,6m) в 2003 г. было снижение этого показателя до 10,8m. Эта максимальная интенсивность роста продажи данного продукта в 2002 г. и последующее снижение в 2003 г. отображает показатель темпа наращивания, %: 16,5 < 18,7 > 17,4.
Цепные темпы роста показывают затухание интенсивности реализации данной продукции из года в год: 116,5 > 116,1 > 112,9.
Все эти показания анализируемого ряда динамики позволяют сделать предположения о возможном применении в аналитическом выравнивании параболы второго порядка:
![]() (3.2)
(3.2)
Таким образом, на основе статистических показателей изменений уровней анализируемого ряда динамики сделано предположение о возможном применении в аналитическом выравнивании исходных данных двух математических функций (3.1) и (3.2).
Для решения вопроса о том, какая их них является адекватной, может применяться критерий минимальности стандартной ошибки аппроксимации:
 (3.3)
(3.3)
Для этого, прежде всего, должны быть решены выбранные математические функции.
Для определения параметров уравнений (3.1) и (3.2) составляется матрица расчетных показателей (таблица 3.2).
Таблица 3.2
При St=0
| Год, квартал |
|
|
|
|
|
| |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 2000 2001 2002 2003 | I II III IV I II III IV I II III IV I II III IV | -15 -13 -11 -9 -7 -5 -3 -1 1 3 5 7 9 11 13 15 | 225 169 121 81 49 25 9 1 1 9 25 49 81 121 169 225 | 50625 28561 14641 6561 2401 625 81 1 1 81 625 2401 6561 14641 28561 50625 | 49,9 75,8 73,9 48,5 48,1 92,3 93,4 55,1 50,9 106,5 108,8 68,8 60,7 120,6 126,7 70,5 | -748,5 -985,4 -812,9 -436,5 -336,7 -461,5 -280,2 -55,1 50,9 319,5 544,0 481,6 546,3 1326,6 1647,1 1057,5 | 11227,5 12810,2 8941,9 3928,5 2356,9 2307,5 840,6 55,1 50,9 958,5 2720,0 3371,2 4916,7 14592,6 21412,3 15862,5 |
| S | 16 | 0 | 1360 | 206992 | 1250,5 | 1856,7 | 106352,9 |
Рассчитаем параметры линейной функции:
![]()
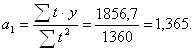
Уравнение линейной функции примет вид:
![]() (3.4)
(3.4)
По модели (3.4) производится расчет теоретических уровней тренда для каждого периода анализируемого ряда динамики ![]() :
:
2000 г. 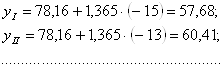
2003 г. ![]()
Полученные теоретические значения уровней тренда ![]() записаны в гр. 4 табл. 3.3.
записаны в гр. 4 табл. 3.3.
Рассчитаем параметры для функции параболы второго порядка:
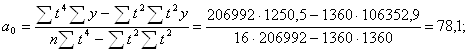
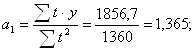
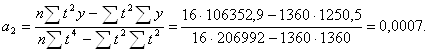
Уравнение параболы второго порядка примет вид:
![]() (3.5)
(3.5)
По модели (3.5) рассчитываются теоретические уровни для каждого периода анализируемого ряда динамики ![]() :
:
2000 г. 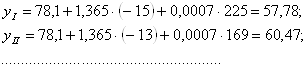
2003 г. ![]()
Полученные теоретические уровни тренда записаны в гр. 5 табл. 3.3.
Для определения показаний стандартной ошибки аппроксимации составляется матрица расчетных показателей (табл. 3.3).
Таблица 3.3
Матрица расчетных показателей для определения стандартной ошибки аппроксимации
| Год, квартал |
|
| Теоретические уровни тренда по моделям | Отклонения теоретических уровней | ||||
| прямоли-нейной функции | параболы второго порядка | прямолинейной функции | параболы второго порядка | |||||
|
|
|
|
| |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2000 | ||||||||
| I II | -15 -13 -11 -9 | 49,9 75,8 73,9 48,5 | 57,68 60,41 63,14 65,88 | 57,78 60,47 63,17 65,87 | 7,78 -15,39 -10,76 17,38 | 60,5 236,8 115,8 302,1 | 7,88 -15,33 -10,73 17,37 | 62,1 235,0 115,1 301,7 |
| 2001 | ||||||||
| I II | -7 -5 -3 -1 | 48,1 92,3 93,4 55,1 | 68,61 71,34 74,07 76,79 | 68,58 71,29 74,00 76,74 | 20,51 -20,96 -19,33 21,69 | 420,7 439,3 373,6 470,5 | 20,48 -21,00 -19,40 21,64 | 419,4 411,2 376,4 468,3 |
| 2002 | ||||||||
| I II | 1 3 5 7 | 50,9 106,5 108,8 68,8 | 79,52 82,25 84,98 87,72 | 79,47 82,20 84,94 87,69 | 28,62 -24,25 -23,82 18,92 | 819,2 588,1 567,4 357,0 | 28,57 -24,30 -23,86 18,89 | 816,2 590,5 569,3 356,8 |
| 2003 | ||||||||
| I II | 9 11 13 15 | 60,7 120,6 126,7 70,5 | 90,45 93,18 95,91 98,63 | 90,44 93,20 95,96 98,73 | 29,75 -27,42 -30,19 28,13 | 885,1 751,8 929,5 791,3 | 29,74 -27,40 -30,74 28,23 | 884,5 750,8 944,9 796,9 |
| S | 0 | 1250,5 | 1250,56 | 1250,53 | ´ | 8109,7 | ´ | 8129,1 |
По итоговым данным гр. 7 и 9 табл. 3.3 определяется по формуле (3.3) ошибка аппроксимации ![]() :
:
1) для модели ![]()
![]() :
:
2) для модели ![]()
![]()
Из сравнения вычисленных значений стандартной ошибки аппроксимации следует, что по критерию минимальности предпочтительнее будет трендовая модель (3.4), синтезированная на основе прямолинейной функции (3.1).
Поэтому определение индексов сезонности реализации данной продукции следует осуществлять на базе теоретических уровней тренда, вычисленных по модели (3.4): ![]() .
.
Теоретические уровни тренда анализируемого ряда динамики изображены на графике (см. рис. 3.1) в виде пунктирной прямой линии.
Для определения индексов сезонности ![]() используется следующая матрица расчетных показателей (таблица 3.4).
используется следующая матрица расчетных показателей (таблица 3.4).
Таблица 3.4
| Год, квартал |
|
|
| Год, квартал |
|
|
| |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| 2000 | 2002 | |||||||
| I | 49,9 75,8 73,9 48,5 | 57,68 60,44 63,15 65,88 | 86,5 125,4 117,0 73,6 | I | 50,9 106,5 108,8 68,8 | 79,52 82,25 84,98 87,72 | 64,0 129,5 128,0 78,4 | |
| 2001 | 2003 | |||||||
| I | 48,1 92,3 93,4 55,1 | 68,61 71,34 74,07 76,79 | 70,1 129,4 126,1 71,8 | I | 60,7 120,6 126,7 70,5 | 90,45 93,18 95,91 98,63 | 67,1 129,4 132,1 71,5 |
В гр. 4 таблицы 3.4 определены индивидуальные индексы сезонности ![]() , характеризующие отношение эмпирических уровней
, характеризующие отношение эмпирических уровней ![]() к теоретическим
к теоретическим ![]() для каждого периода анализируемого ряда внутригодовой динамики.
для каждого периода анализируемого ряда внутригодовой динамики.
Для элиминирования действия факторов случайного порядка производится усреднение индивидуальных индексов сезонности. Для этого по формуле ![]() производится расчет средних индексов сезонности по одноименным кварталам
производится расчет средних индексов сезонности по одноименным кварталам ![]() анализируемого ряда внутригодовой динамики:
анализируемого ряда внутригодовой динамики:
I кв.: ![]()
II кв.: ![]() (3.6)
(3.6)
III кв.: ![]()
IV кв.: ![]()
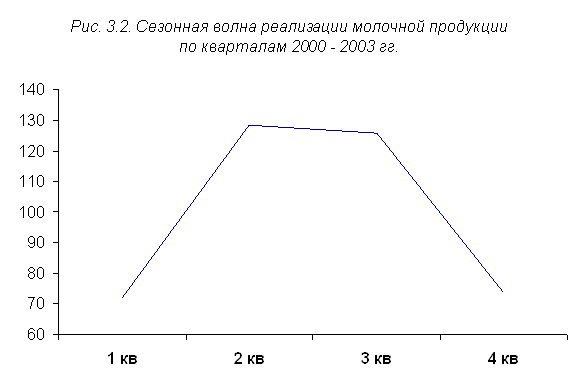
Вычисленные средние индексы сезонности (3.6) составляют модель сезонной волны реализации молочной продукции во внутригодовом цикле.
Наибольший объем продаж приходится на II и III кварталы с превышением среднегодового уровня соответственно на 28,4 и 25,8%. В I и IV кварталах происходит снижение среднегодового уровня соответственно на 28,1 и 26,2%.
Более наглядно полученная модель сезонной волны может быть представлена графически (рис. 3.2).
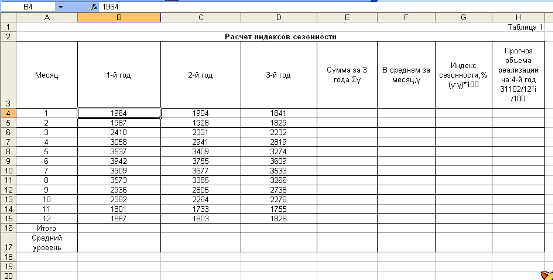
Покажем расчет индексов сезонности способом постоянной средней на примере данных о товарообороте торгового предприятия (табл. 3.5).
Таблица 3.5
Среднедневной товарооборот, тыс. руб.
| Месяц | 2001 г. | 2002 г. | 2003 г. |
| 1 | 2 | 3 | 4 |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 68,4 69,3 70,9 71,1 64,3 92,9 91,0 71,3 75,7 66,7 63,1 73,3 | 72,8 73,4 73,5 75,4 63,2 98,4 82,4 65,0 75,9 68,2 63,8 74,0 | 65,1 66,5 74,4 73,6 67,2 100,0 90,0 72,6 68,9 70,4 66,3 77,2 |
| В среднем за год | 73,4 | 73,8 | 74,4 |
Необходимо определить индексы сезонности товарооборота.
Так как среднегодовой темп роста составил ![]() , то в данном случае нет значительной тенденции роста. Следовательно, используем способ постоянной средней.
, то в данном случае нет значительной тенденции роста. Следовательно, используем способ постоянной средней.
Исчислим средние уровни одноименных внутригодовых периодов ![]() :
:
для января ![]() тыс. руб.;
тыс. руб.;
для февраля ![]() тыс. руб. и т. д.
тыс. руб. и т. д.
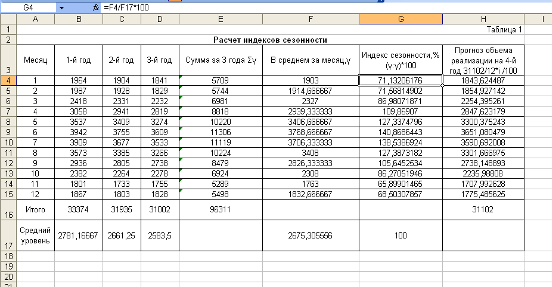
Для каждого месяца эти значения определены в гр. 6 табл. 3.6.
Таблица 3.6
| Месяц | Уровни, тыс. руб. | Расчетные графы | ||||
| 2001 г. | 2002 г. | 2003 г. |
|
|
| |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 68,4 69,3 70,9 71,1 64,3 92,9 91,0 71,3 75,7 66,7 63,1 73,3 | 72,8 73,4 73,5 75,4 63,2 98,4 82,4 65,0 75,9 68,2 63,8 74,0 | 65,1 66,5 74,4 73,6 67,2 100,0 90,0 72,6 68,9 70,4 66,3 77,2 | 206,3 209,2 218,8 220,1 194,7 291,3 264,2 211,9 220,5 205,3 193,2 224,5 | 68,8 69,7 72,9 73,4 64,9 97,1 88,1 70,6 73,5 68,4 64,4 74,8 | 93,1 94,3 98,6 99,3 87,8 131,4 119,2 95,5 99,5 92,6 87,1 101,2 |
| S | 881,0 | 886,0 | 893,0 | 2660,0 | 73,9 | 100,0 |
В итоговой строке гр. 6 определен знаменатель формулы (2.4) в виде общего для всего ряда динамики среднего уровня ![]() :
:
![]() тыс. руб.
тыс. руб.
Этот общий средний уровень и используется в качестве постоянной базы сравнения при определении средних индексов сезонности, которые помещены в гр. 7 табл. 3.6:
![]() ;
;
![]() и т. д.
и т. д.
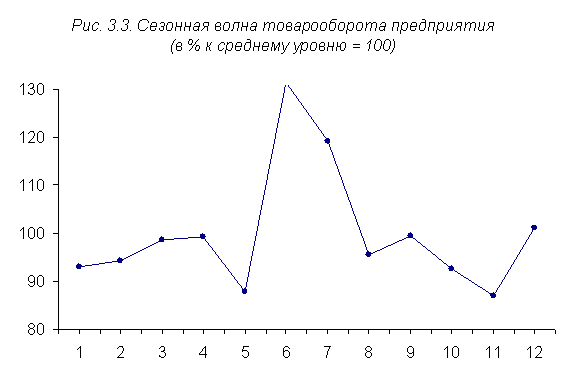
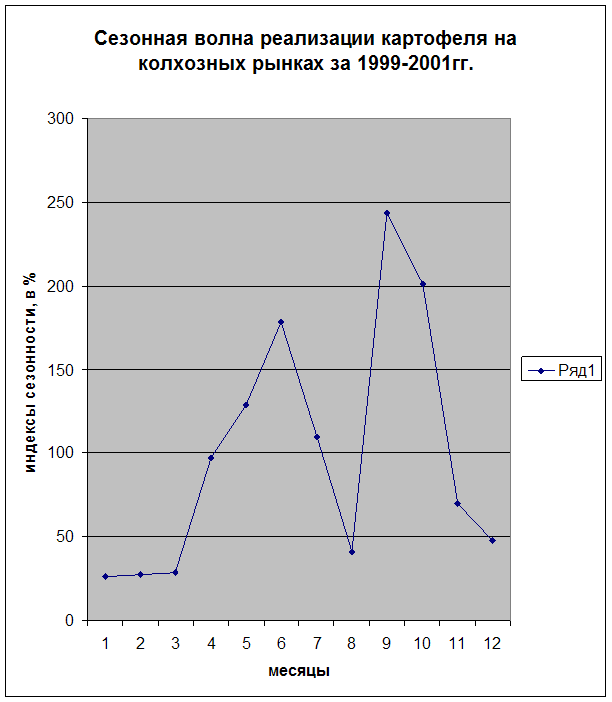
Из гр. 7 видно, что сезонные колебания товарооборота предприятия характеризуются повышением в июне (+31,4%), июле (+19,2%) и декабре (+1,2%) и снижением в других месяцах.
Для большей наглядности сезонных колебаний средние индексы изобразим графически (рис. 3.3).
Для выявления сезонных колебаний можно применить метод скользящей средней.
Средние индексы сезонности в этом случае определяются по формуле:
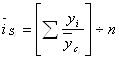 (3.7)
(3.7)
где ![]() - исходные уровни ряда;
- исходные уровни ряда; ![]() - сглаженные уровни ряда;
- сглаженные уровни ряда; ![]() - число одноименных периодов.
- число одноименных периодов.
Имеются данные о реализации продукции сельскохозяйственного производства в одном из магазинов г. Тюмени (табл. 3.7).
Таблица 3.7
| Квартал | 2000 | 2001 | 2002 | 2003 |
| 1 | 2 | 3 | 4 | 5 |
| I II III IV | 165 253 316 287 | 237 288 356 331 | 410 431 443 389 | 416 439 472 450 |
Сглаженные уровни и индексы сезонности рассчитаны в таблице 3.8.
Таблица 3.8
| Год, квартал |
|
|
| Год, квартал |
|
|
| |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| 2000 | 2002 | |||||||
| I | 165 253 316 287 | - - 264,25 277,6 | - - 119,6 103,4 | I | 410 431 443 389 | 392,9 411,0 419,0 420,75 | 104,4 104,9 105,7 92,5 | |
| 2001 | 2003 | |||||||
| I | 237 288 356 331 | 287,0 297,5 324,6 364,1 | 82,6 96,8 109,7 90,9 | I | 416 439 472 450 | 425,37 436,62 - - | 97,8 100,5 - - |
Для получения средних индексов сезонности ![]() производится осреднение исчисленных значений
производится осреднение исчисленных значений ![]() :
:![]() по одноименным кварталам:
по одноименным кварталам:
I кв.: ![]()
II кв.: ![]()
III кв.: ![]()
IV кв.: ![]()
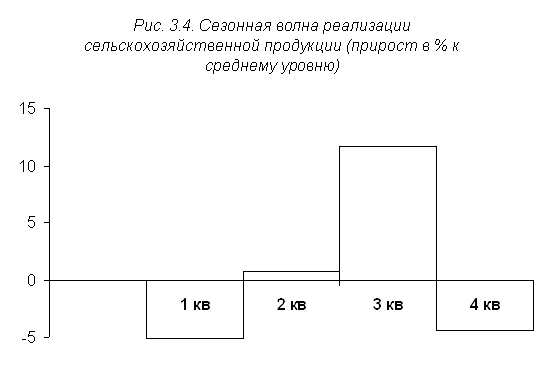
Исчисленные показатели являются средними индексами сезонных колебаний продажи продукции сельскохозяйственного производства по кварталам.
Для наглядности сезонные колебания изобразим на графике (рис. 3.4).
Похожие работы
... В заключении подведем итоги. Сезонные колебания – периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку. Существуют различные методы изучения сезонности. Как с предварительным определением и исключением общей тенденции, так и без предварительного выравнивания. Наиболее простой способ определения сезонной волны без предварительного выравнивания – ...
... - на июнь. Прогнозирование уровней ряда в данном случае проводят путем умножения выровненных месячных уровней на индексы сезонности. Аналитическая часть Статистическое изучение сезонности реализации товаров и услуг. Валовой внутренний продукт один из важнейших показателей системы национальных счетов, характеризующий конечный результат производственной деятельности экономических единиц - ...
... 100,147 104,623 110,409 115,973 112,561 123,639 Таблица 3 – Построение модели сезонной волны на основе гармоник ряда Фурье (1 вариант). Удельный розничный товарооборот области по месяцам y cos t y sin t yt y cos 2t y sin 2t yt y cos 3t y sin 3t yt y cos 4t y sin 4t yt 158,68 158,68 0 166,242 158,68 0 170,618 158,68 0 ...
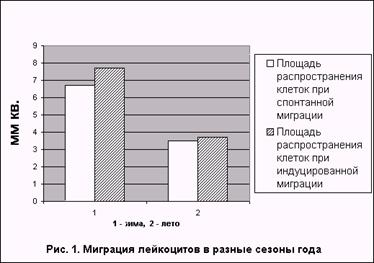
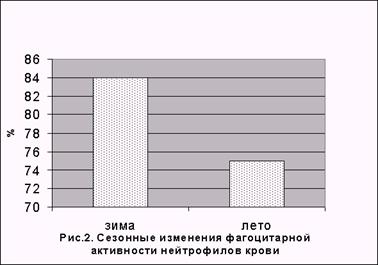
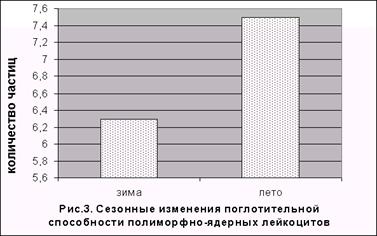
... свойств и реактивности лейкоцитов интактных лабораторных крыс в зимний и летний периоды показал наличие сезонных колебаний неспецифических физиологических реакций белых клеток крови. В летние месяцы установлено существенное снижение общей локомоционной а фагоцитарной активности полиморфно-ядерных лейкоцитов (рис. 1 и 2): площадь распространения клеток при спонтанной и стимулированной миграции в ...
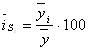

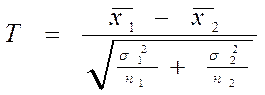
0 комментариев