Навигация
Метод наименьших квадратов для однофакторной линейной регрессии
1. Метод наименьших квадратов для однофакторной линейной регрессии
Линейная регрессия находит широкое применение в эконометрике в виде четкой эконометрической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида:
Ŷ = а + bx или Ŷ = a + bx + ε;
Уравнение вида Ŷ = а + bx позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора X. На графике теоретические значения представляют линию регрессии.

|
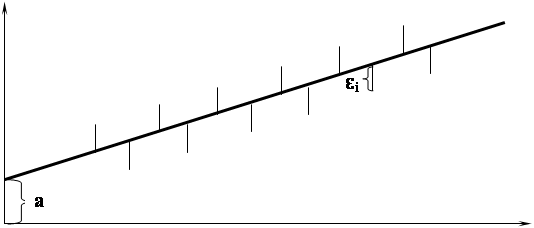
Рисунок 1 – Графическая оценка параметров линейной регрессии
Построение линейной регрессии сводится к оценке ее параметров – а и b. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратится к полю корреляции и, выбрав на графике две точки, провести через них прямую линию. Далее по графику можно определить значения параметров. Параметр a определим как точку пересечения линии регрессии с осью OY, а параметр b оценим, исходя из угла наклона линии регрессии, как dy/dx, где dy – приращение результата y, а dx – приращение фактора x, т.е. Ŷ = а + bx.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов(МНК).
МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака (y) от расчетных (теоретических) минимальна:
∑(Yi – Ŷ xi)2 → min
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной.
εi = Yi– Ŷxi.
следовательно ∑εi2 → min
 | |||
| |||
|
Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю.
Обозначим ∑εi2 через S, тогда
S = ∑ (Y–Ŷ xi)2 =∑(Y-a-bx)2;
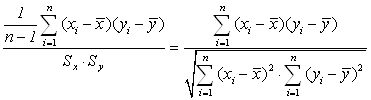
Дифференцируем данное выражение, решаем систему нормальных уравнений, получаем следующую формулу расчета оценки параметра b:
b = (ух – у•x)/(x2-x2).
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Например, если в функции издержек Ŷ = 3000 + 2x (где x – количество единиц продукции, у – издержки, тыс. грн.) с увеличением объема продукции на 1 ед. издержки производства возрастают в среднем на 2 тыс. грн., т.е. дополнительный прирост продукции на ед. потребует увеличения затрат в среднем на 2 тыс. грн.
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
2. Найти коэффициент эластичности для указанной модели в заданной точке X. Сделать экономический анализ.
Модель: Y = (2/X) + 5; X = 0;
Известно, что коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Формула расчета коэффициента эластичности:
Э = f′(x) X/Y,
где f′(x) – первая производная, характеризующая соотношение прироста результата и фактора для соответствующей формы связи.
Y = (2/X) + 5,
f′(x) = -2/x2;
Следовательно получим следующее математическое выражение
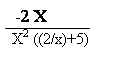 |
| |||
![]()
|
При заданном значении X = 0 получим, что коэффициент эластичности равен Э = -1.
Допустим, что заданная функция Y = (2/X) + 5 определяет зависимость спроса от цены. В этом случае с ростом цены на 1% спрос снижается в среднем на 1%.
3. Убыточность выращивания овощей в сельскохозяйственных предприятиях и уровни факторов (сбор овощей с 1 га, ц и затраты труда, человеко-часов на 1 ц), ее формирующих, характеризуются следующими данными за год:| № района | Фактор | Уровень убыточности, % | |
| Сбор овощей с 1 га, ц | Затраты труда, человеко-часов на 1 ц | ||
| 1 | 93,2 | 2,3 | 8,8 |
| 2 | 65,9 | 26,8 | 39,4 |
| 3 | 44,6 | 22,8 | 26,2 |
| 4 | 18,7 | 56,6 | 78,8 |
| 5 | 64,6 | 16,4 | 34 |
| 6 | 25,6 | 26,5 | 47,6 |
| 7 | 47,2 | 26 | 43,7 |
| 8 | 48,2 | 12,4 | 23,6 |
| 9 | 64,1 | 10 | 19,9 |
| 10 | 30,3 | 41,7 | 50 |
| 11 | 28,4 | 47,9 | 63,1 |
| 12 | 47,8 | 32,4 | 44,2 |
| 13 | 101,3 | 20,2 | 11,2 |
| 14 | 31,4 | 39,6 | 52,8 |
| 15 | 67,6 | 18,4 | 20,2 |
Нелинейную зависимость принять![]()
Задание №1
Построим линейную зависимость показателя от первого фактора.
Обозначим: сбор овощей с 1 Га как X1, а уровень убыточности как Y.
| Сбор овощей с 1 га, ц | Уровень убыточности, % |
| X1 | Y |
| 93,2 | 8,8 |
| 65,9 | 39,4 |
| 44,6 | 26,2 |
| 18,7 | 78,8 |
| 64,6 | 34 |
| 25,6 | 47,6 |
| 47,2 | 43,7 |
| 48,2 | 23,6 |
| 64,1 | 19,9 |
| 30,3 | 50 |
| 28,4 | 63,1 |
| 47,8 | 44,2 |
| 101,3 | 11,2 |
| 31,4 | 52,8 |
| 67,6 | 20,2 |
Найдем основные числовые характеристики.
1. Объем выборки n = 15 – суммарное число наблюдений.
2. Минимальное значение величины сбора овощей Х=18,7;
Максимальное значение сбора овощей Х=101,3;
Минимальное значение величины уровня убыточности Y=8,8;
Максимальное значение величины уровня убыточности Y=78,8;
3. ![]() Среднее значение:
Среднее значение:
X = ∑xi.
Среднее значение величины сбора овощей X = 778,9/15 = 51,926.
Среднее значение величины уровня убыточности Y = 563,5/15 = 37,566.
Похожие работы
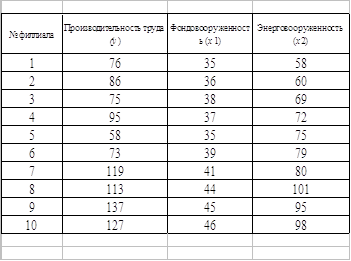
... № 2 Результаты обследования десяти статистически однородных филиалов фирмы в таблице (цифры условные). Требуется: А. Построить модель парной линейной прогрессии производительности труда от фактора фондовооруженности, определить коэффициент регрессии, рассчитать парный коэффициент корреляции, оценить тесноту корреляционной связи, найти коэффициент эластичности и бета – коэффициент: пояснить ...
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...
... относятся: метод взаимосвязанных параллельных рядов, балансовый метод, индексный метод, метод аналитических группировок, корреляционные таблицы и графический метод. Метод взаимосвязанных параллельных рядов состоит в установлении связей между экономическими явлениями посредством сопоставления показателей двух или нескольких рядов. Для этого признак-фактор ранжируется, т.е. располагается в порядке ...
... : Вычисляем среднеквадратическое отклонение: Далее определяем коэффициент вариации: Выводы: в процессе выполнения лабораторной работы были изучены принципы и методы отбора образцов, проб и выборок при исследовании свойств текстильных материалов, способы вычисления основных статистических характеристик. Были определены структурные характеристики, поверхностная плотность и толщина кожи ...

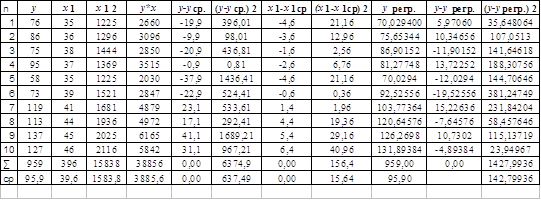

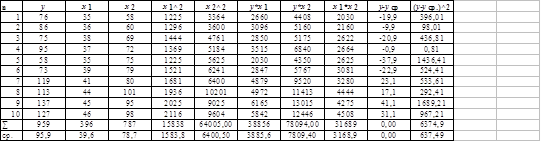

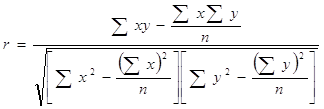
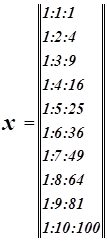

0 комментариев