Навигация
4. Дисперсия
 | |||
 | |||
D(X) = ∑ (Xi – X)2 = 254,66 D(Y) = ∑(Yi – Y)2 = 385,56
5. Среднеквадратическое отклонение:
![]()
![]() σx=√254,66 = 15,95 значит среднее трудоемкости в среднем от среднего значения составляет 15,95%.
σx=√254,66 = 15,95 значит среднее трудоемкости в среднем от среднего значения составляет 15,95%.
σy=√385.17 = 19.63, значит среднее уровня убыточности всей сельскохозяйственной продукции в среднем от среднего значения составляет 19,63%.
Для начала нужно определить, связаны ли X1 и Y между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания). Точка с координатами (X, Y) = (26,816; 37,566) называется центром рассеяния. По виде корреляционного поля можно предположить, что зависимость между X1 и Y нелинейная (стр.), а именно имеет зависимость ![]() .
.
Путем преобразования нелинейную зависимость приведем к линейной V = b0 + b1U.
Для начала заменим переменные U = x, а V = ln(Y).
Найдем конкретные значения V и U (стр.), затем строим корреляционное поле (стр.) и находим результаты регрессивной статистики.
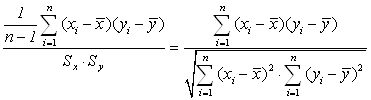
Для определения тесноты линейной связи V = b0 + b1U найдем коэффициент корреляции:
![]()
∑(Ui – U) (Vi – V)
|
Так как 0,6 ≤ rxy <0,9 то линейная связь между X1 и Y – достаточная. Попытаемся описать связь между X1 и Y зависимостью Y=b0+b1X. Параметры b0, b1 найдем по МНК.
и1 = кчн σн. σч = -0,856 х 19,63. 24,25 = -0,696;
b0 = y – b1X = 37.566 + 0.696 х 51.92 = 73.70
Так как b1 < 0, то зависимость между X1 и Y обратная: с ростом сбора овощей уровень убыточности сельскохозяйственной продукции падает. Проверим значимость коэффициентов b0, b1.
Значимость коэффициентов b может быть проверена с помощью критерия Стьюдента:
tнабл = b0/σb0 = 73.70/6.53 = 11.28;
tнабл = b1/σb1 = -0,696/0,1146 = -6,0716;
Значимость tнабл равна 0,000039, т.е. 0,0039%. Так как это значение меньше 5%, то коэффициент b1 статистически значим.
Получили модель связи сбора овощей и уровня убыточности сельскохозяйственной продукции:
Y = 73.70 – 0.6960X
После того, как была построена модель, необходимо проверить ее на адекватность.
Разброс данных, объясняемый регрессией SSR = ∑(ỹ-y)2 = 3990,5;
Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25;
Общий разброс данных SSY = ∑(yi-y)2 = 5397,85;
Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192;
Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками.
Вывод: Качество модели хорошее
Проверим с помощью критерия Фишера. Для проверки этой гипотезы сравниваются между собой величины:
MSR = SSR / K1 = 3990.5946/ K1 = 3990.5946. Отсюда K1 = 1.
MSE = SSE / K2 = 1407.25 / K2 = 108.25. Отсюда K2 = 13.
Находим наблюдаемое значение критерия Фишера Fнабл= MSR/MSE.
Значимость этого значения α = 0,00004, т.е. процент ошибки равен 0,004%. Так как это значение меньше 5%, то найденная модель считается адекватной.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза [18.7; 101.3]. Допустим это точка X1 = 50.
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза Y(х = 50) = 73.7085 – 0.6960 х 50 = 38.9.
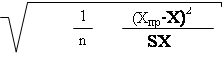
Найдем полуширину доверительного интервала в каждой точке выборки Xпр
 | |||
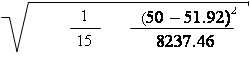 | |||
δ = σе ty1 + + = 10.4 × 2.016 1 + +
Отсюда получим, что δ = 23,20.
В приведенной формуле:
![]()
![]()
![]()
![]()
![]() σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
σе = MSE = 108.25 = 10.40 – среднеквадратичное отклонение выборочных точек от линии регрессии.
ty= 2,16 – критическая точка распределения Стъюдента для надежности γ = 0,95 и K2 = 13 при n = 15.
SX = ∑(xi-x)2 или
SX = (n – 1) х D(X) = 14 х 588 х 39 = 8237,46;
Прогнозируемый доверительный интервал для любого X1 такой (ỹ – δ; ỹ + δ).
Совокупность доверительных интервалов для всех X1 из области прогнозов образует доверительную область, которая представляет область заключения между двумя гиперболами. Наиболее узкое место в точке X.
Прогноз для Х1 составит от 15,7 до 62,1 с гарантией 95%. То есть можно сказать, что при сборе овощей 50 центнеров с 1 га уровень убыточности сельскохозяйственной продукции можно спрогнозировать на уровне 15,7% – 62,1%.
Найдем эластичность Y = 73.70 – 0.6960X.
В нашем случае (для линейной модели) Ex = -0.6960X/(73.70 – 0.6960X).
В численном выражении это составит:
Eх=50 = -0,6960×50 / (73.70 – 0.6960×50) = – 0,8946;
Коэффициент эластичности показывает, что при изменении величины Х1 на 1% показатель Y уменьшается на 0,8946%.
Например, если Х1 = 50,5 (т.е. увеличился на 1%), то Y = 38.9 + 38.9×(-0,008946) = 38,5520006.
Проверим и Yх =50,5 = 73.70 – 0.6960X = 73.70 – 0.6960 × 50,50 = 38,552.
Похожие работы
... № 2 Результаты обследования десяти статистически однородных филиалов фирмы в таблице (цифры условные). Требуется: А. Построить модель парной линейной прогрессии производительности труда от фактора фондовооруженности, определить коэффициент регрессии, рассчитать парный коэффициент корреляции, оценить тесноту корреляционной связи, найти коэффициент эластичности и бета – коэффициент: пояснить ...
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...
... относятся: метод взаимосвязанных параллельных рядов, балансовый метод, индексный метод, метод аналитических группировок, корреляционные таблицы и графический метод. Метод взаимосвязанных параллельных рядов состоит в установлении связей между экономическими явлениями посредством сопоставления показателей двух или нескольких рядов. Для этого признак-фактор ранжируется, т.е. располагается в порядке ...
... : Вычисляем среднеквадратическое отклонение: Далее определяем коэффициент вариации: Выводы: в процессе выполнения лабораторной работы были изучены принципы и методы отбора образцов, проб и выборок при исследовании свойств текстильных материалов, способы вычисления основных статистических характеристик. Были определены структурные характеристики, поверхностная плотность и толщина кожи ...

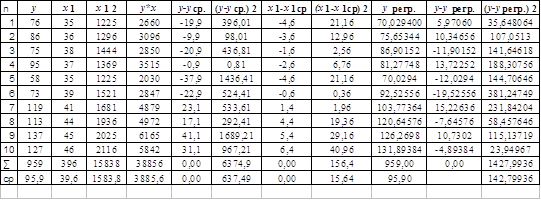

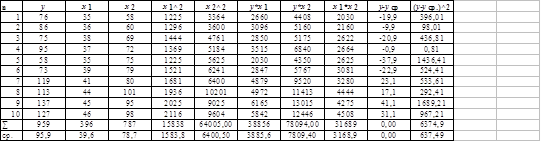

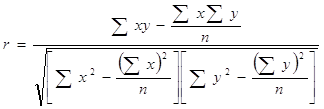
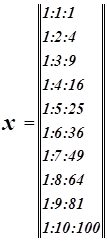

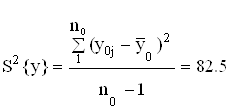
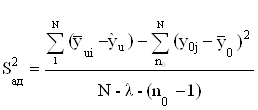
0 комментариев