Навигация
Аналитическая группировка, характеризующая зависимость между территориальным и результативным признаком
3. Аналитическая группировка, характеризующая зависимость между территориальным и результативным признаком
Таблица 2
| Название федерального округа | Кол-во регионов | Численность населения | Средняя продолжительность жизни при рождении | Изменение средней ожидаемой жизни при рождение по сравнению с группой с минимальной ожидаемой продолжительностью жизни при рождение |
| Центральный | 17 | 37545,8 | 64,59 | 104,3 |
| Северо-Западный | 10 | 13731 | 62,19 | 100,4 |
| Южный | 13 | 22820,8 | 68,26 | 110,2 |
| Приволжский | 14 | 30710,2 | 65,16 | 105,2 |
| Уральский | 4 | 12279,2 | 64,67 | 104,4 |
| Сибирский | 12 | 19794,2 | 62,06 | 100,2 |
| Дальневосточный | 9 | 6593 | 61,95 | 103,5 |
| Итого: | 79 | 143474,2 | 448,89 | 728,2 |
| № группы |
|
|
| V | Выводы об однородности данных в группах |
| 1 | 64,59 | 2,05 | 4,19 | 3,17% | Коэффициент вариации V=σ/x * 100% < 17% следовательно данные абсолютно однородны |
| 2 | 62,19 | 1,61 | 2,58 | 2,58% | |
| 3 | 68,26 | 2,58 | 6,66 | 3,78% | |
| 4 | 65,16 | 1,33 | 1,78 | 2,05% | |
| 5 | 64,67 | 0,88 | 0,78 | 1,36% | |
| 6 | 62,06 | 3,21 | 10,28 | 5,17% | |
| 7 | 61,95 | 1,40 | 1,97 | 0,02% |
|

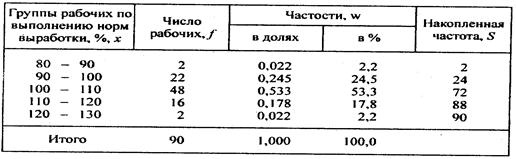
4. Построить вариационный ряд, характеризующий распределение регионов(стран) по величине признака, указанного в варианте (Уровень заболеваемости (на 1000 человек населения) болезни органов дыхания)
| Группа регионов по уровню заболеваемости (на 1000 человек населения): болезни органов дыхания% | Число регионов в группе | Среднее значение исследуемого признака | ||
| 1 | 180,6 | 230,4 | 12 | 210,125 |
| 2 | 230,4 | 266,6 | 12 | 249,208 |
| 3 | 266,6 | 277,4 | 11 | 273,155 |
| 4 | 277,4 | 317,2 | 14 | 303,692 |
| 5 | 317,2 | 348,2 | 14 | 328,179 |
| 6 | 348,2 | 439,8 | 14 | 383,750 |
| Итого: | 77 | |||
Анализ однородности данных в группах
| № группы |
|
|
| V | Выводы об однородности данных в группах |
| 1 | 210,13 | 15,10 | 227,97 | 7,19% | Коэффициент вариации V=σ/x * 100% < 17% следовательно данные абсолютно однородны |
| 2 | 249,21 | 11,83 | 139,88 | 4,75% | |
| 3 | 273,16 | 3,01 | 9,09 | 1,10% | |
| 4 | 303,69 | 8,32 | 69,27 | 2,74% | |
| 5 | 328,18 | 3,02 | 9,12 | 0,92% | |
| 6 | 383,75 | 27,67 | 765,85 | 7,21% |
Для построенного ряда определим:
· показатели центра распределения
· показатели вариации
· показатели дифференциации и концентрации
· показатели формы распределения
По результатам расчетов сделаем вывод о характере распределения регионов по величине признака.
Показатели центра распределения:
К показателям центра распределения относятся: средняя арифметическая, мода и медиана.
| Номер группы | 1 | 2 | 3 | 4 | 5 | 6 |
| Центр интервала, x’ | 205,5 | 248,5 | 272 | 297,3 | 332,7 | 394 |
| Число регионов в группе, f | 12 | 12 | 11 | 14 | 14 | 14 |
Средняя арифметическая –
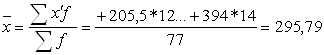 %
%
Мода – наиболее часто встречающееся значение признака. Так как данный ряд имеет неравные интервалы, то модальным будет интервал с максимальной плотностью распределения.
| Номер интервала (группы) | 1 | 2 | 3 | 4 | 5 | 6 |
| Плотность распределения, p | 0,24 | 0,33 | 1,02 | 0,35 | 0,45 | 0,15 |
| Длина интервала, i | 49,8 | 36,2 | 10,8 | 39,8 | 31 | 91,6 |
| Накопленная частота, F | 12 | 24 | 34 | 38 | 52 | 66 |
Мода находится в 3 интервале (наибольшая плотность распределения, равная 1,02, соответствует именно ему). Конкретное значение моды определяется по формуле:

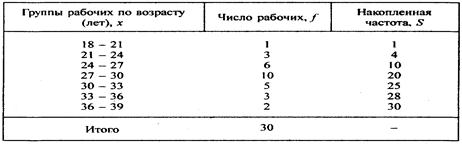
Медиана соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется её номером:
![]()
Следовательно, медианным является 5-ый интервал 317,2–348,2. Численное же значение медианы определяется по формуле:
 319,414%
319,414%
ВЫВОД: в качестве показателя центра распределения можно выбрать любой из полученных показателей, т. к. их численные значения примерно равны.
Показатели вариации (колеблемости) признака:
Абсолютные показатели:
Размах колебаний (размах вариации):
R=Xmax-Xmin
R= 439,8–180,6 = 259,2
Для расчета показателей вариации построим дополнительную таблицу:
| Группа регионов по уровню заболеваемости (на 1000 человек населения): болезни органов дыхания | Число регионов, f | x' | x' * f | d =| x' – x | | d*f | d2 * f | ||
| 180,6 | 230,4 | 12 | 90,3 | 1083,6 | 205,49 | 2465,88 | 506713,68 | |
| 230,4 | 266,6 | 12 | 115,2 | 1382,4 | 180,59 | 2167,08 | 391352,98 | |
| 266,6 | 277,4 | 11 | 133,3 | 1466,3 | 162,49 | 1787,39 | 290433,00 | |
| 277,4 | 317,2 | 14 | 138,7 | 1941,8 | 157,09 | 2199,26 | 345481,75 | |
| 317,2 | 348,2 | 14 | 158,6 | 2220,4 | 137,19 | 1920,66 | 263495,35 | |
| 348,2 | 439,8 | 14 | 174,1 | 2437,4 | 121,69 | 1703,66 | 207318,39 | |
| Итого: | 77 | 10531,9 | 964,54 | 12243,93 | 2004795,14 | |||
Среднее линейное отклонение:
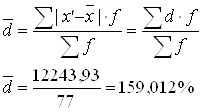
Дисперсия:

Среднее квадратичное отклонение:
![]() %
%
Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
Квартильное отклонение:
Квартиль – значения признака, которые делят ранжированный ряд на четыре равные по численности части.
Сначала определим положение квартилей:
![]() Это 2 ой интервал 230,4 – 266,6
Это 2 ой интервал 230,4 – 266,6
![]()
Это 3 ий интервал 266,6 – 277,4
![]()
Это 4 интервал 277,4 – 317,2
Теперь найдём значение квартилей:
![]() , где
, где
xQ – нижняя граница интервала, в котором находится квартиль
SQ-1 – накопленная частота интервала, предшествующего тому, в котором находится квартиль
fQ – частота интервала, в котором находится квартиль
Итак,
![]()
![]()
![]()
![]()
Квартильное отклонение применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений.
Относительные показатели вариации:
Коэффициент осцилляции:
![]()
Коэффициент вариации:
![]()
Вывод: совокупность данных является однородной, т. к. коэффициент вариации не превышает 33%.
Относительное линейное отклонение:
![]()
Относительный показатель квартильной вариации:
![]()
Показатели дифференциации и концентрации:
Для оценки дифференциации используем фондовый коэффициент дифференциации и коэффициент децильной дифференциации.
Фондовый коэффициент дифференциации.
8 регионов – 10% от общего числа регионов.
Среднее значение признака для 10% самых мелких единиц совокупности (180,6; 189,2; 199; 202,9; 210,1; 213,8; 215,1; 223,3; 224,4; 229,5):
![]() 208,28
208,28
Среднее значение признака для 10% самых крупных единиц совокупности (369,5; 372; 372,8; 384,4; 394,3; 396; 398,4; 399,3; 437,7; 439,8):
![]() 396,46
396,46
![]()
Коэффициент децильной дифференциации.
![]() – номер первой децили. Она находится в 1-ом интервале 180,6 – 230,4
– номер первой децили. Она находится в 1-ом интервале 180,6 – 230,4
![]()
![]() – номер девятой децили. Она находится в 5-ом интервале 317,2 – 348,2
– номер девятой децили. Она находится в 5-ом интервале 317,2 – 348,2
![]()
![]()
Вывод: наименьший показатель признака 10% регионов с наибольшими значениями по уровню заболеваемости на 1000 человек населения: болезни органов дыхания в 5,48 раза выше наивысшего показателя уровня заболеваемости на 1000 человек населения: болезни органов дыхания 10% регионов с наименьшими значениями признака.
Для оценки концентрации единиц по значению признака используем коэффициент концентрации Джинни и коэффициент Герфендаля.
Коэффициент Джинни:
![]()
![]()
Концентрацию можно считать несущественной, т. к. 0,08<0,3
Коэффициент Герфендаля (фактический):
![]() =
= ![]() 0,179
0,179
Коэффициент Герфендаля при равномерном распределении:
![]() , где 6 – число интервалов;
, где 6 – число интервалов; ![]()
Сравним фактическое значение коэффициента Герфендаля с рассчитанным значением коэффициента для равномерного распределения. Т.к. 0,179 > 0,167, то концентрация очень высокая.
Показатели формы распределения.
Относительный показатель асимметрии:
![]()
Величина показателя асимметрии положительна, следовательно асимметрия правосторонняя.
Рассчитаем показатель асимметрии другим способом:
![]()
 523514,77
523514,77
![]() 2,62
2,62
Средняя квадратическая ошибка асимметрии:
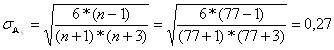
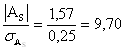
Вывод: с вероятностью 99,7% асимметрия существенна (так как 9,70 > 3) и распределение признака в генеральной совокупности не является симметричным. Вследствие несимметричности распределения показатели эксцесса не рассчитываются.
Похожие работы
... Методы научных исследований - это те приемы и средства, с помощью которых ученые получают достоверные сведения, используемые далее для построения научных теорий и выработки практических рекомендаций. Сила науки во многом зависит от совершенства методов исследования, от того насколько они валидны и надежны, как быстро и эффективно данная отрасль знаний способна воспринять и использовать у себя ...
... дел документов первичного учёта работы прокуроров, следователей, дознавателей. Учётные данные, подлежащие включению в отчёты, проверяются с точки зрения их полноты и достоверности по документам первичного учёта. В органах внутренних дел и прокуратуры установлены и другие формы отчётности, отражающие различные стороны их деятельности. Основным звеном судебной системы является районный суд, с ...
... основными производственными фондами (факторный признак - х) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение. 5. ПРАКТИКУМ ПО ТЕОРИИ СТАТИСТИКИ 1. ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ И ЕЕ РОЛЬ В АНАЛИЗЕ ИНФОРМАЦИИ Одним из основных наиболее распространенных методов обработки и анализа первичной статистической информации ...
... где n – число групп; N – число единиц совокупности. Построим группировку с помощью данного метода для таблицы 1.2. Для этого: 1. данные таблицы 1.2 проранжируем и представим в таблице 3.1: Таблица 3.1 Ранжированный ряд количества магазинов по розничному товарообороту в республике Калмыкия, млн. руб. 121 208 234 234 238 239 256 280 299 309 341 342 388 390 400 456 547 ...

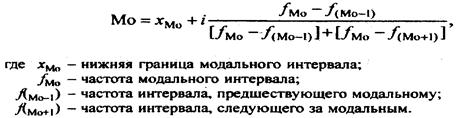
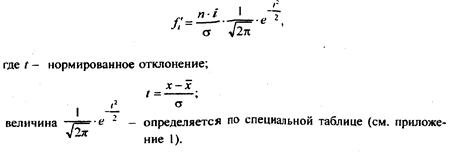




0 комментариев