Ранжирование и группировка данных в статистике

Задача №1

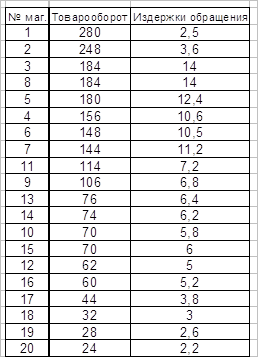
Работа двадцати предприятий пищевой промышленности

В отчетном периоде характеризуется следующими данными:

Таблица 1

№	1	2
1	10	11,8
2	11	12,4
3	12,6	13,8
4	13	15,1
5	14,2	16,4
6	15	17
7	15,5	17,3
8	16,3	18,1
9	17,7	19,6
10	19,3	23,1
11	10,8	12
12	12,2	13
13	12,8	12,9
14	13,5	15,6
15	14,6	16,8
16	15,3	18,2
17	16	17,9
18	17,1	10
19	18	18
20	20	27,2

1-Среднегодовая стоимость промышленно-производственных ОФ, млн. руб.

2-Товарная продукция в сопоставимых оптовых ценах предприятия, млн. руб.

1.  Проведите ранжирование исходных данных по размеру ОФ и их группировку, образовав 5 групп с равновеликими интервалами. Приведите расчет равновеликого интервала группировки по формуле:

H=Xmax-Xmin/n

 

2.  Определите по каждой группе:

– число заводов;

– стоимость ОПФ-всего и в среднем на один завод:

– стоимость ТП-всего и в среднем на один завод.

Результаты представьте в табличном виде, проанализирйте их и сделайте выводы

H=20–10/5=2

где x_max, x_min – максимальное и минимальное значения кредитных вложений

Определим теперь интервалы групп (x_i, x_i+1):

1 группа: 10–12 млн. руб.

2 группа: 12–14 млн. руб.

3 группа: 14–16 млн. руб.

4 группа: 16–18 млн. руб.

5 группа: 18–20 млн. руб.

Далее упорядочим исходную таблицу по возрастанию ОФ

№	Группа	Среднегодовая стоимость промышленно – производственных ОФ в группе, млн. руб.	Товарная продукция в сопоставимых оптовых ценах предприятия, млн. руб.
1	10,1–12	10	11,8
		11	12,4
		10,8	12
2	12,1–14	12,6	13,8
		13	15,1
		12,2	13
		12,8	12,9
		13,5	15,6
3	14,1–16	14,2	16,4
		15	17
		15,5	17,3
		14,6	16,8
		15,3	18,2
		16	17,9
4	16,1–18	16,3	18,1
		17,7	19,6
		17,1	10
		18	18
5	18,1–20	19,3	23,1
		20	27,2

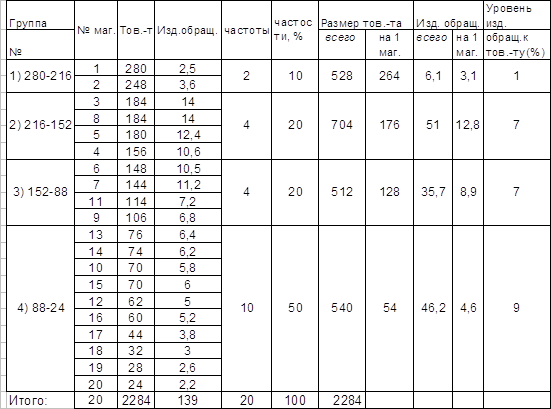
На основе полученной таблицы определим требуемые показатели. Результаты представим в виде групповой таблицы:

Таблица 1.2

Группа	Количество заводов в группе, шт.	Среднегодовая стоимость промышленно – производственных ОПФ, млн. руб.	Стоимость промышленно – производственных ОПФ, млн. руб.		Товарная продукция в сопоставимых оптовых ценах предприятия, млн. руб.
1	3	10–12	Всего	31,8	Всего	36,2
			В среднем на один завод	10,6	В среднем на один завод	12,067
2	5	12,1–14	Всего	64,1	Всего	70,4
			В среднем на один завод	12,82	В среднем на один завод	14,08
3	6	14,1–16	Всего	90,6	Всего	103,6
			В среднем на один завод	15,1	В среднем на один завод	17,27
4	4	16,1–18	Всего	69,1	Всего	65,7
			В среднем на один завод	17,275	В среднем на один завод	17,275
5	2	18,1–20	Всего	39,3	Всего	50,3
			В среднем на один завод	19,65	В среднем на один завод	25,15

Задача №4

Имеются данные по трем предприятиям, вырабатывающие однородную продукцию:

№	Базисный год		Отчетный год
	Затрата времени на ед. продукции, час	Выпущено продукции, тыс. ед.	Затраты времени на ед. продукции, тыс. ед.	Затраты времени на всю продукцию, ч
1	0,34	52,1	0,34	19975
2	0,48	45,7	0,48	22248
3	0,53	23,8	0,53	13462

Обоснуйте выбор формул средней и по этим формулам определите средние затраты времени на продукцию по трем предприятиям в базисном и отчетном годах, сравните полученные результаты и сделайте выводы.

Решение

Средние затраты времени определяются по формуле:

,

где V – затраты времени на единицу продукции; S – затраты времени на всю продукцию. Определим средние затраты времени на 3 предприятиях. Т.к. заданы затраты времени на единицу продукции и затраты времени на всю продукцию то:

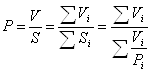
Данная формула называется средней гармонической взвешенной.

Подставив в последнюю формулу известные значения, получим средние затраты времени на производство на предприятиях в отчетном году:

P=19975+22248+13462/(19972/0,34+22248/0,48+13462/0,53)= 0,427 ч

Определим средние затраты времени на производства продукции в базисном году:

Данная формула называется средней арифметической взвешенной.

Подставив в последнюю формулу известные значения, получим затраты времени на производство продукции в базисном году:

P=(0,34*52,1+0,48*45,7+0,53*23,8)/(52,1+45,7+23,8)= 0,4298=0,43 ч

Вывод: средние затраты времени на производство продукции в базисном и отчетном году отличаются на (0,43–0,427)*100%= 0,003*100%=0,3%

 

Задача №9

 

В результате контрольной выборочной проверки расфасовки чая осуществлена 25% механическая выборка по способу бесповторного отбора, в результате которой получено следующее распределение пачек чая по массе:

Масса пачки чая, г	Число пачек чая, шт.
До 49	17
49–50	52
50–51	21
51–52	7
52 и выше	3
ИТОГО	100

По результатам выборочного обследования определите:

1.  Среднюю массу пачки чая;

2.  Дисперсию и среднее квадратичное отклонение;

3.  Коэффициент вариации;

4.  С вероятностью 0,997 возможные пределы средней массы пачки чая во всей партии продукции;

5.  С вероятностью 0,954 возможные пределы удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции.

Решение

Приведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы. Результаты представлены в таблице:

Масса пачки чая, г	Масса пачки чая, г	Средняя масса пачки чая, г	Число пачек чая, шт
До 49	48–49	48,5	17
От 49 до 50	49–50	49,5	52
От 50 до 51	50–51	50,5	21
От 51 до 52	51–52	51,5	7
Свыше 52	52–53	52,5	3
Итого			100

Среднюю массу пачки чая находим по формуле средней арифметической взвешенной:

Подставив в последнюю формулу известные значения, получим среднюю массу пачки чая:

Y=(48.5*17+49.5*52+50.5*21+51.5*7+52.5*3)/100=49.77 г.

Дисперсия определяется по формуле:

.

Подставив в последнюю формулу известные значения, получим дисперсию:

s²=((48,5–49,77)²*17+(49,5–49,77)²*52+(50,5–49,77)²*21+(51,5–49,77)²*7+(52,5–49,77)²)/100=85,71/100=0,8571 г.²

Среднее квадратическое отклонение равно:

S=√s²=√0,8571=0,93 г.

Коэффициент вариации определяется по формуле:

V=s/y=0,93/49,77= 0,019*100%=1,9%

Рассчитаем сначала предельную ошибку выборки. Так при вероятности p = 0,997 коэффициент доверия t = 3. Поскольку дана 25%-ная случайная бесповторная выборка, то

n/N=0,25

где n – объем выборочной совокупности, N – объем генеральной совокупности.

Считаем также, что дисперсия s²=0,8571. Тогда предельная ошибка выборочной средней равна:

Δy=t*√σ²/n*(1-n/N)=3*√0,8571/100*(1–0,25)=0,24 г.

Определим теперь возможные границы, в которых ожидается средняя масса чая на 1 пакетик чая

y – Δy≤my≤y+ Δy

49,77–0,8571≤my≤49,77+0,8571

48,9129≤my≤50,6271

Т.е., с вероятностью 0,997 можно утверждать, что масса чая на 1 пакетик находится в пределах 48,9129 до 50,6271

Выборочная доля w удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции с вероятностью 0,954 равна.

W=(48+3)/100=0,51=51 г.

Учитывая, что при вероятности p = 0,954 коэффициент доверия t = 2, вычислим предельную ошибку выборочной доли:

Δw= t*√(w*(1-w)/n) *(1-n/N)=2*√(0,51*(1–0,51)/100)*(1–0,25)=0,086г

или

Пределы доли признака во всей совокупности:

51–8,6≤d≤51+8,6

42,4≤d≤59,6

Таким образом, с вероятностью 0,954 можно утверждать, что границы удельного веса пачек чая находятся в пределах42,4г до 59,6г во всей продукции.

Выводы: