Навигация
Гистограмма и полигон распределения предприятий по проценту выполнения за первое полугодие приведены на рисунках
5. Гистограмма и полигон распределения предприятий по проценту выполнения за первое полугодие приведены на рисунках.
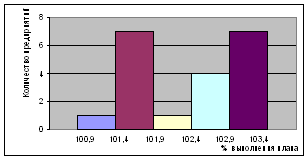
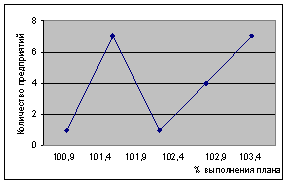
Рисунок 7 – Полигон и гистограмма распределение по проценту выполнения плана
В среднем по полугодиям план перевыполнялся на 2,06%.
ЗАДАЧА 4
По исходным данным:
• построить корреляционную таблицу;
• рассчитать коэффициент корреляции.
По исходным данным построим корреляционную таблицу основных показателей ремонтных предприятий железнодорожного транспорта (таблица 4.1).
Таблица 4.1 – Корреляционная таблица основных показателей ремонтных предприятий железнодорожного транспорта
| Объем валовой продукции млн у.е. | Среднегодовая стоимость основных фондов млн у.е. | |||||||
| 1,5 - 3,1 | 3,1 - 4,7 | 4,7 - 6,3 | 6,3 - 7,9 | 7,9 - 9,5 | Итого: | |||
| от | до | |||||||
| 2 | 3 | 7 | 4 | 11 | ||||
| 3 | 4 | 5 | 4 | 9 | ||||
| 4 | 5 | 12 | 12 | |||||
| 5 | 6 | 4 | 14 | 18 | ||||
| Итого: | 12 | 8 | 0 | 16 | 14 | 50 | ||
Рассчитаем коэффициент корреляции по формуле:
 .
.
![]() = 209,7 / 50 = ,19
= 209,7 / 50 = ,19 ![]() = 299,9 / 50 = 6,00
= 299,9 / 50 = 6,00
Для расчёта коэффициента корреляции воспользуемся вспомогательной таблицей 4.2.
Таблица 4.2 – Расчёт коэффициента корреляции
| №п/я | X | Y |
|
| ( | ( | ( |
| 51 | 4,7 | 3,4 | -1,30 | -0,79 | 1,03 | 1,68 | 0,63 |
| 52 | 4,5 | 3,3 | -1,50 | -0,89 | 1,34 | 2,24 | 0,80 |
| 53 | 4,2 | 3,1 | -1,80 | -1,09 | 1,97 | 3,23 | 1,20 |
| 54 | 6,6 | 4,3 | 0,60 | 0,11 | 0,06 | 0,36 | 0,01 |
| 55 | 7,0 | 4,6 | 1,00 | 0,41 | 0,41 | 1,00 | 0,16 |
| 56 | 7,3 | 4,8 | 1,30 | 0,61 | 0,79 | 1,70 | 0,37 |
| 57 | 7,6 | 5,0 | 1,60 | 0,81 | 1,29 | 2,57 | 0,65 |
| 58 | 6,7 | 4,3 | 0,70 | 0,11 | 0,07 | 0,49 | 0,01 |
| 59 | 7,9 | 5,2 | 1,90 | 1,01 | 1,91 | 3,62 | 1,01 |
| 60 | 7,2 | 4,8 | 1,20 | 0,61 | 0,73 | 1,44 | 0,37 |
| 61 | 8,3 | 5,2 | 2,30 | 1,01 | 2,32 | 5,30 | 1,01 |
| 62 | 7,4 | 4,9 | 1,40 | 0,71 | 0,99 | 1,97 | 0,50 |
| 63 | 6,8 | 4,5 | 0,80 | 0,31 | 0,25 | 0,64 | 0,09 |
| 64 | 8,6 | 5,3 | 2,60 | 1,11 | 2,88 | 6,77 | 1,22 |
| 65 | 7,1 | 4,6 | 1,10 | 0,41 | 0,45 | 1,21 | 0,16 |
| 66 | 7,7 | 6,0 | 1,70 | 1,81 | 3,07 | 2,90 | 3,26 |
| 67 | 7,5 | 4,9 | 1,50 | 0,71 | 1,06 | 2,26 | 0,50 |
| 68 | 6,9 | 4,5 | 0,90 | 0,31 | 0,28 | 0,81 | 0,09 |
| 69 | 9,0 | 5,5 | 3,00 | 1,31 | 3,92 | 9,01 | 1,71 |
| 70 | 7,1 | 4,7 | 1,10 | 0,51 | 0,56 | 1,21 | 0,26 |
| 71 | 8,5 | 5,5 | 2,50 | 1,31 | 3,27 | 6,26 | 1,71 |
| 72 | 8,0 | 5,3 | 2,00 | 1,11 | 2,21 | 4,01 | 1,22 |
| 73 | 7,8 | 5,1 | 1,80 | 0,91 | 1,63 | 3,25 | 0,82 |
| 74 | 8,8 | 5,4 | 2,80 | 1,21 | 3,38 | 7,85 | 1,45 |
| 75 | 8,1 | 5,3 | 2,10 | 1,11 | 2,32 | 4,42 | 1,22 |
| 76 | 8,7 | 5,4 | 2,70 | 1,21 | 3,26 | 7,30 | 1,45 |
| 77 | 7,7 | 5,1 | 1,70 | 0,91 | 1,54 | 2,90 | 0,82 |
| 78 | 8,9 | 5,4 | 2,90 | 1,21 | 3,50 | 8,42 | 1,45 |
| 79 | 9,1 | 5,4 | 3,10 | 1,21 | 3,74 | 9,62 | 1,45 |
| 80 | 9,3 | 5,5 | 3,30 | 1,31 | 4,31 | 10,90 | 1,71 |
| 81 | 9,2 | 5,6 | 3,20 | 1,41 | 4,50 | 10,25 | 1,98 |
| 82 | 9,4 | 5,7 | 3,40 | 1,51 | 5,12 | 11,57 | 2,27 |
| 83 | 9,5 | 5,7 | 3,50 | 1,51 | 5,27 | 12,26 | 2,27 |
| 84 | 2,6 | 2,0 | -3,40 | -2,19 | 7,46 | 11,55 | 4,81 |
| 85 | 4,6 | 3,3 | -1,40 | -0,89 | 1,25 | 1,95 | 0,80 |
| 86 | 2,6 | 2,0 | -3,40 | -2,19 | 7,46 | 11,55 | 4,81 |
| 87 | 3,3 | 2,1 | -2,70 | -2,09 | 5,65 | 7,28 | 4,38 |
| 88 | 3,1 | 2,3 | -2,90 | -1,89 | 5,49 | 8,40 | 3,59 |
| 89 | 4,1 | 2,9 | -1,90 | -1,29 | 2,46 | 3,60 | 1,67 |
| 90 | 3,8 | 2,6 | -2,20 | -1,59 | 3,50 | 4,83 | 2,54 |
| 91 | 3,3 | 2,3 | -2,70 | -1,89 | 5,11 | 7,28 | 3,59 |
| 92 | 2,4 | 3,5 | -3,60 | -0,69 | 2,50 | 12,95 | 0,48 |
| 93 | 2,8 | 4,0 | -3,20 | -0,19 | 0,62 | 10,23 | 0,04 |
| 94 | 2,4 | 3,3 | -3,60 | -0,89 | 3,22 | 12,95 | 0,80 |
| 95 | 1,5 | 2,1 | -4,50 | -2,09 | 9,42 | 20,23 | 4,38 |
| 96 | 2,0 | 2,7 | -4,00 | -1,49 | 5,97 | 15,98 | 2,23 |
| 97 | 1,6 | 2,1 | -4,40 | -2,09 | 9,21 | 19,34 | 4,38 |
| 98 | 2,0 | 2,7 | -4,00 | -1,49 | 5,97 | 15,98 | 2,23 |
| 99 | 2,4 | 3,4 | -3,60 | -0,79 | 2,86 | 12,95 | 0,63 |
| 100 | 2,3 | 3,1 | -3,70 | -1,09 | 4,05 | 13,68 | 1,20 |
| 50 | 299,90 | 209,70 | 151,62 | 205,89 | 76,43 |
После промежуточных расчётов рассчитаем коэффициент корреляции по приведённой формуле.
![]()
В результате получим Rxy = 1,209. По данному значению коэффициента можно сделать вывод, что между исследуемыми величинами существует высокая зависимость.
Литература
1. Быченко О.Г. Общая теория статистики: Задание на контрольную работу №1 с методическими указаниями. – Гомель: БелГУТ, 2000. – 30 с.
2. Быченко О.Г. Общая теория статистики: Задание на контрольную работу №2 с методическими указаниями. – Гомель: БелГУТ, 2000. – 31с.
Похожие работы
... , состояния собственных оборотных средств, сверхнормативных остатков товарно-материальных ценностей, источников образования фондов экономического стимулирования и их использования. Основными задачами статистики финансов предприятий являются: Изучение состояния и развития финансово-денежных отношений хозяйствующих субъектов; Анализ объема и структуры источников формирования финансовых ресурсов; ...
... предприятия, то есть его способности своевременно, из собственных средств возмещать затраты, вложенные в основной и оборотный капитал, и расплачиваться по своим обязательствам. Поэтому в статистике финансов предприятий регулярно, начиная с 1993 г., рассчитывается ряд показателей, характеризующих финансовое состояние предприятий, и производится группировка предприятий по уровню их текущей ...
жирва 14,52 270 1 270 273 276 256 240 всего 660 459,3 463,56 457,9 440,9 415,05 2)Выполнение плана по выпуску молока в условно-натуральном выражении: 1 год = 4 квартала. Молоко 1%=49,21+44,4+51,8+37=182,141 - по факту. Молоко 1,5%=141,35+137,5+133,1=411,95 - по факту. Молоко 2,7%=270+273+276+256=1075 - по факту. Молоко 1%=51,8*4=202,7 – по плану. Молоко 1,5%=137,5*4=550 ...
... оборудования 2 ~ текущий ремонт оборудования 1 ~ капитальный ремонт заводских зданий 20 ~ монтаж металлоконструкций по заказу со стороны 5 электростанцией произведено электроэнергии 50 ~ использовано на промышленно-производственные нужды 40 ~ отпущено жилому комплексу 10 остатки готовой продукции на складе на начало месяца 25 остатки готовой продукции на складе на конец месяца 20 ...


0 комментариев