Парная корреляция и парная линейная регрессия
Оценка значимости параметров взаимосвязи
Определение инфляции. Открытая и подавленная форма инфляции. Измерение инфляции
Основные методики расчета индексов, их преимущества и недостатки
Статистика цен и расчёт ИПЦ в РФ
Инфляция в России
Рассчитываем коэффициент корреляции ранга
Навигация
Оценка значимости параметров взаимосвязи
Статистическое изучение взаимосвязи социально-экономических явлений
60033
знака
8
таблиц
5
изображений
3. Оценка значимости параметров взаимосвязи
Получив оценки корреляции и регрессии, необходимо проверить их на соответствие истинным параметрам взаимосвязи.
Существующие программы для ЭВМ включают, как правило, несколько наиболее распространенных критериев. Для оценки значимости коэффициента парной корреляции рассчитывают стандартную ошибку коэффициента корреляции:
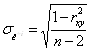(11)
В первом приближении нужно, чтобы
. Значимость rxy проверяется его сопоставлением с
, при этом получают
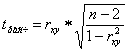(12)
где tрасч – так называемое расчетное значение t-критерия.
Если tрасч больше теоретического (табличного) значения критерия Стьюдента (tтабл) для заданного уровня вероятности и (n-2) степеней свободы, то можно утверждать, что rxy значимо.
Подобным же образом на основе соответствующих формул рассчитывают стандартные ошибки параметров уравнения регрессии, а затем и t-критерии для каждого параметра. Важно опять-таки проверить, чтобы соблюдалось условие tрасч > tтабл. В противном случае доверять полученной оценке параметра нет оснований.
Вывод о правильности выбора вида взаимосвязи и характеристику значимости всего уравнения регрессии получают с помощью F-критерия, вычисляя его расчетное значение:
(13)
где n – число наблюдений; m – число параметров уравнения регрессии.
Fрасч также должно быть больше Fтеор при v1 = (m-1) и v2 = (n-m) степенях свободы. В противном случае следует пересмотреть форму уравнения, перечень переменных и т.д.
4. Непараметрические методы оценки связи
Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических методов.
Между тем в статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили название непараметрических.
Если изучается взаимосвязь двух качественных признаков, то используют комбинационное распределение единиц совокупности в форме так называемых таблиц взаимной сопряженности.
Рассмотрим методику анализа таблиц взаимной сопряженности на конкретном примере социальной мобильности как процесса преодоления замкнутости отдельных социальных и профессиональных групп населения. Ниже приведены данные о распределении выпускников средних школ по сферам занятости с выделением аналогичных общественных групп их родителей.
| Занятия родителей | Число детей, занятых в | Всего | |||
| Промышлен- ности и стро- ительстве | сельском хозяйстве | сфере обслужи- вания | сфере интел- лектуального труда | ||
| 1. Промышленность и строительство 2. Сельское хозяйство 3. Сфера обслуживания 4. Сфера интеллектуального труда | 40 34 16 24 | 5 29 6 5 | 7 13 15 9 | 39 12 19 72 | 91 88 56 110 |
| Всего | 114 | 45 | 44 | 142 | 345 |
Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности: 42,9 % детей родителей группы 1 ("Промышленность и строительство") заняты в сфере интеллектуального труда (39 из 91); 38,9 % детей. родители которых трудятся в сельском хозяйстве, работают в промышленности (34 из 88) и т.д.
Можно заметить и явную наследственность в передаче профессий. Так, из пришедших в сельское хозяйство 29 человек, или 64,4 %, являются детьми работников сельского хозяйства; более чем у 50 % в сфере интеллектуального труда родители относятся к той же социальной группе и т.д.
Однако важно получить обобщающий показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях. Для этой цели исчисляют, например, коэффициенты взаимной сопряженности Пирсона (С) и Чупрова (К):
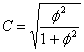и 
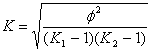(14)
где f2 – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:
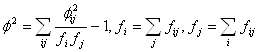(15)
К1 и К2 – число групп по каждому из признаков. Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, колеблется в обычных для этих показателей пределах от 0 до 1.
В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д.
При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Например, если у 5-й и 6-й единиц совокупности значения признаков одинаковы, обе получат ранг, равный (5 + 6) / 2 = 5,5.
Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (r) и Кендэлла (t). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.
ИНФЛЯЦИЯ
Похожие работы
... (13) и (15) значения, сравниваются с критическими tк, которые принимаются согласно данным таблицы Стьюдента с учетом заданного уровня значимости (a) и числа степеней свободы (k = n - 2). В социально-экономических исследованиях уровень значимости a обычно принимают равным 5%, т.е. a = 0,05, что соответствует доверительной вероятности 95%. Параметр признается существенным при условии, если tф > ...
... особого этапа статистического исследования – сводки. Сводка – это характеристика выделенных групп и совокупности в целом с помощью статистических показателей. Статистический показатель – это обобщающая характеристика социально-экономических явлений и процессов в конкретных условиях места и времени. Обобщающие показатели могут быть представлены абсолютными, относительными и средними величинами. ...
... исследуемых объектов, приводит к изменению установившихся причинно-следственных связей. Именно поэтому изучение структуры и структурных сдвигов занимает важное место в курсе теории статистики. В статистике под структурой понимают совокупность единиц, обладающих определенной устойчивостью внутригрупповых связей при сохранении основных признаков, характеризующих эту совокупность как целое. Основные ...
... с Программой социально-экономического развития РФ должен быть завершен переход к формированию и предоставлению официальной статистической информации на основе ОКВЭД. 2 Взаимосвязь показателей деятельности предприятия Статистические показатели - представляют собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. Система ...
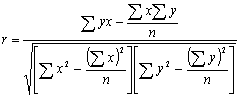
0 комментариев