Навигация
Измерим тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения
2. Измерим тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения.
Сделаем выводы.
Решение:
1. а) Чтобы установить наличие и характер связи между фондом заработной платы и среднегодовой заработной платой методом аналитической группировки, построим группировку по факторному признаку (фонд заработной платы).
Ширина интервала для факторного признака равна:
![]() (млн. руб.)
(млн. руб.)
Сначала для того, чтобы составить рабочую таблицу, в которой в каждой строчке будут данные отдельно по каждой организации и итоговые данные по выделенным группам, а затем для составления итоговой аналитической таблицы, в которой будут сведения только по группам в целом, следует использовать макет.
Макет – это таблица, состоящая из строк и граф, которые еще не заполнены цифрами.
Таблица 5
| № п/п | Группы организаций по размеру фонда заработной платы, млн. руб. | Число организаций | Фонд заработной платы, млн. руб. | Среднесписочная численность работников, чел. | Среднегодовая заработная плата, тыс. руб. | |
| всего | в среднем на 1 организацию | всего | в среднем на 1 организацию | |||
| 1 2… | ||||||
| Итого | ||||||
Строим рабочую таблицу:
Таблица 6
| № п/п | Группы организаций по размеру фонда заработной платы, млн. Руб. | № организации | Фонд заработной платы, млн. Руб. | Среднесписочная численность работников, чел. | Среднегодовая заработная плата, тыс. Руб. | Расчетная графа |
| Хi | Уi | (yi- | ||||
| 1 | 4,32 - 8,736 | 2 | 8,112 | 156 | 52 | 825,029 |
| 6 | 8,532 | 158 | 54 | 714,136 | ||
| 15 | 4,320 | 120 | 36 | 2000,175 | ||
| 20 | 5,850 | 130 | 45 | 1276,155 | ||
| ИТОГО | 4 | 26,814 | 564 | 47,543 | - | |
| 2 | 8,736 - 13,152 | 1 | 11,340 | 162 | 70 | 114,989 |
| 5 | 13,035 | 165 | 79 | 2,970 | ||
| 9 | 12,062 | 163 | 74 | 45,203 | ||
| 10 | 9,540 | 159 | 60 | 429,456 | ||
| 14 | 10,465 | 161 | 65 | 247,223 | ||
| 16 | 11,502 | 162 | 71 | 94,543 | ||
| 18 | 12,792 | 164 | 78 | 7,416 | ||
| 21 | 9,858 | 159 | 62 | 350,562 | ||
| 22 | 11,826 | 162 | 73 | 59,650 | ||
| 24 | 8,848 | 158 | 56 | 611,242 | ||
| 29 | 10,948 | 161 | 68 | 161,883 | ||
| ИТОГО | 11 | 122,216 | 1776 | 68,815 | - | |
| 3 | 13,152 - 17,568 | 3 | 15,036 | 179 | 84 | 10,737 |
| 8 | 17,100 | 190 | 90 | 86,057 | ||
| 11 | 13,694 | 167 | 82 | 1,630 | ||
| 13 | 16,082 | 187 | 86 | 27,843 | ||
| 17 | 16,356 | 188 | 87 | 39,397 | ||
| 19 | 17,472 | 192 | 91 | 105,610 | ||
| 25 | 13,944 | 168 | 83 | 5,183 | ||
| 27 | 13,280 | 166 | 80 | 0,523 | ||
| 30 | 15,810 | 186 | 85 | 18,290 | ||
| ИТОГО | 9 | 138,774 | 1623 | 85,505 | - | |
| 4 | 17,568 - 21,984 | 4 | 19,012 | 194 | 98 | 298,484 |
| 12 | 21,320 | 205 | 104 | 541,804 | ||
| 23 | 18,142 | 193 | 94 | 176,270 | ||
| ИТОГО | 3 | 58,474 | 592 | 98,774 | - | |
| 5 | 21,984 - 26,4 | 7 | 26,400 | 220 | 120 | 1542,658 |
| 26 | 23,920 | 208 | 115 | 1174,891 | ||
| 28 | 22,356 | 207 | 108 | 744,018 | ||
| ИТОГО | 3 | 72,676 | 635 | 114,450 | - | |
| ВСЕГО | 30 | 418,954 | 5190 | - | 11714,027 |
Для установления наличия и характера связи между размером фонда заработной платы и уровнем заработной платы по данным рабочей таблицы строим итоговую аналитическую таблицу:
Таблица 7.
| № п/п | Группы организаций по размеру фонда заработной платы, млн. руб. | Число организаций | Фонд заработной платы, млн. руб. | Среднесписочная численность работников, чел. | Среднегодовая заработная плата, тыс. руб. | |
| всего | в среднем на 1 организацию | всего | в среднем на 1 организацию | |||
| nj | xj |
| zj |
| ||
| 1 2 3 4 5 | 4,32 – 8,736 8,736 – 13,152 13,152 – 17,568 17,568 – 21,984 21,984 – 26,4 | 4 11 9 3 3 | 26,814 122,216 138,774 58,474 72,676 | 6,704 11,111 15,419 19,491 24,225 | 564 1776 1623 592 635 | 47,543 68,815 85,505 98,774 114,450 |
| ИТОГО | 30 | 418,954 |
| 5190 |
| |
Вычисляем в каждой группе среднее значение факторного признака ![]() и среднее значение результативного признака
и среднее значение результативного признака ![]() по формулам:
по формулам:
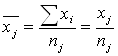
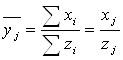
где nj – число единиц в j-той группе.
Szi = zi и Sхi=хj- это соответственно численность работников и фонд заработной платы в j-той группе.
Вычислим общее среднее значение каждого признака в совокупности:
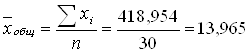 (млн. руб.)
(млн. руб.)
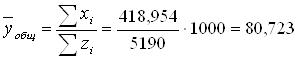 (тыс. руб.)
(тыс. руб.)
Общее среднее значение каждого признака в совокупности можно вычислить и другим способом, как среднее арифметическое взвешенное из средних групповых ![]() и
и ![]() (весом является число предприятий в каждой группе njи численность работников в группе zi):
(весом является число предприятий в каждой группе njи численность работников в группе zi):

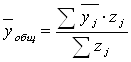
![]() (млн. руб.)
(млн. руб.)
![]() (млн.руб.)
(млн.руб.)
Сравниваем изменения ![]() от группы к группе с изменениями
от группы к группе с изменениями ![]() от группы к группе. Среднее значение результативного признака систематически изменяется вслед за средним значением факторного признака, следовательно, делаем вывод о том, что связь между ними существует. Причем с ростом фонда заработной платы среднегодовая заработная плата также увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная зависимость.
от группы к группе. Среднее значение результативного признака систематически изменяется вслед за средним значением факторного признака, следовательно, делаем вывод о том, что связь между ними существует. Причем с ростом фонда заработной платы среднегодовая заработная плата также увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная зависимость.
Корреляционная связь. При такой связи среднее значение (математическое ожидание) случайной величины результативного признака у закономерно изменяется в зависимости от изменения другой величины х или других случайных величин х1, х2, …, хn. Корреляционная связь проявляется не в каждом отдельном случае, а во всей совокупности в целом. Только при достаточно большом количестве случаев каждому значению случайного признака х будет соответствовать распределение средних значений случайного признака у.
б) Установим наличие и характер связи между фондом заработной платы и среднегодовым уровнем заработной платы методом корреляционной таблицы.
Составим корреляционную таблицу, образовав пять групп с равными интервалами по обоим признакам.
Таблица 8.
| Заработная плата, тыс. руб. Фонд заработной платы, млн. руб. | 36-52,8 | 52,8-69,6 | 69,6-86,4 | 86,4-103,2 | 103,2-120 | Итого |
| 4,32 – 8,736 | 3 | 1 | 4 | |||
| 8,736 – 13,152 | 5 | 6 | 11 | |||
| 13,152 – 17,568 | 6 | 3 | 9 | |||
| 17,568 – 21,984 | 2 | 1 | 3 | |||
| 21,984 – 26,4 | 3 | 3 | ||||
| Итого | 3 | 6 | 12 | 5 | 4 | 30 |
Анализ корреляционной таблицы также свидетельствует о том, что между фондом заработной платы и среднегодовой заработной платой существует прямая корреляционная зависимость.
2. Измерим тесноту связи между исследуемыми признаками с использованием эмпирического корреляционного отношения:
![]()
где ![]() – коэффициент детерминации;
– коэффициент детерминации;
δ2 – межгрупповая дисперсия;
σ2– общая дисперсия.
Межгрупповая дисперсия характеризует вариацию между группами. Ее рассчитываем по формуле:
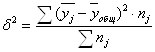
где ![]() – среднее значение результативного признака в j-группе;
– среднее значение результативного признака в j-группе;
![]() – общее среднее значение результативного признака в совокупности;
– общее среднее значение результативного признака в совокупности;
nj – число единиц в j-группе;
j – счетчик групп.
Составим расчетную таблицу:
Таблица 9.
| № п/п | Группы организаций по уровню фонда заработной платы, млн. руб. | Число организаций | Размер заработной платы в среднем на 1 организацию, тыс. руб. | Расчетная графа |
| nj |
| ( | ||
| 1 | 4,32 - 8,736 | 4 | 47,54 | 4403,852 |
| 2 | 8,736 - 13,152 | 11 | 68,82 | 1559,805 |
| 3 | 13,152 - 17,568 | 9 | 85,50 | 205,748 |
| 4 | 17,568 - 21,984 | 3 | 98,77 | 977,444 |
| 5 | 21,984 - 26,4 | 3 | 114,45 | 3412,548 |
| ИТОГО | 30 |
| 10559,396 |
![]()
Нашли дисперсию, характеризующую вариацию размера среднегодовой заработной платы, возникающую под влиянием фонда заработной платы.
Общая дисперсия характеризует вариацию отдельных значений признака относительно общей средней. Ее определяем по формуле:
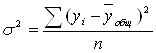
Расчет ![]() представлен в последней графе таблицы №6.
представлен в последней графе таблицы №6.
![]()
Нашли дисперсию, характеризующую вариацию фонда заработной платы, возникающую под влиянием всех причин, действующих на совокупность.
Коэффициент детерминации равен:
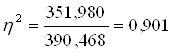
Т.е. 90,1% вариации среднегодовой заработной платы вызывает вариация фонда заработной платы.
Эмпирическое корреляционное отношение составляет:
![]()
Т.к. η > 0,7, то связь между фондом заработной платы и среднегодовой заработной платой очень тесная, т.е. фонд заработной платы сильно влияет на уровень среднегодовой заработной платы.
Значимость коэффициента детерминации можно проверить по критерию Фишера:

где df1 = k – 1 – степень свободы 1;
k - число групп;
df2 = n – k - степень свободы 2;
n – число единиц совокупности.
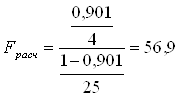
Fтабл. (0,05; 4; 25) = 2,76
Fрасч. > Fтабл. Þ связь между исследуемыми признаками статистически значимая и коэффициент детерминации статистически достоверен.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
1. Ошибку выборки среднегодовой заработной платы и границы, в которых будет находиться уровень среднегодовой заработной платы в генеральной совокупности.
2. Ошибку выборки доли организаций с уровнем среднегодовой заработной платы 86,4 тыс. руб. и более и границы, в которых будет находиться генеральная доля.
Решение:
1. Так как дана 20%-ная, механическая выборка, то ошибку выборки среднего выпуска продукции m определим по формуле:
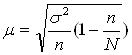
n = 30 (организаций)
![]()
σ2 = 367,1565 (см. задание 1)
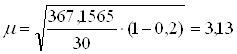 (тыс. руб.)
(тыс. руб.)
Границы, в которых будет находиться средняя заработная плата в генеральной совокупности, определяются следующим образом:
![]()
где ![]() – средняя заработная плата в выборке;
– средняя заработная плата в выборке;
![]() = 80,81 (тыс. руб.)
= 80,81 (тыс. руб.)
D - предельная ошибка выборки.
![]()
где t – коэффициент доверия. Для доверительной вероятности 0,954 он равен: t = 2.
D = 2 * 3,13 = 6,26 (тыс. руб.)
80,81 - 6,26 £ ![]() £ 80,81 + 6,26
£ 80,81 + 6,26
74,55 £ ![]() £ 87,07
£ 87,07
Т.е. с вероятностью 0,954 можно ожидать, что средняя заработная плата в генеральной совокупности находится в пределах от 74,55 до 87,07 тыс. руб.
2. Доля организаций с уровнем заработной платы 86,4 тыс. руб. и более составляет:
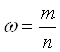
где m – количество организаций с уровнем заработной платы 86,4 тыс. руб. и более.
m = 5 + 4 = 9
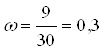 или 30,0%
или 30,0%
Т.е. доля организаций с уровнем заработной платы 86,4 тыс. руб. и более составляет 30% от общего числа организаций в выборке.
Ошибку выборки доли организаций с уровнем заработной платы 86,4 тыс. руб. и более определим по той же формуле:
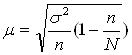
где дисперсия σ2 равна:
σ2 = w * (1 - w) = 0,3 * (1 – 0,3) = 0,21
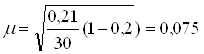
Предельная ошибка выборки составляет:
D = t * m = 2 * 0,075 = 0,15
Границы, в которых будет находиться генеральная доля р, равны:
w - D £ р £ w + D
0,3 – 0,15 £ р £ 0,3 + 0,15
0,15 £ р £ 0,45
Т.е. с вероятностью 0,954 можно ожидать, что доля организаций с уровнем заработной платы 86,4 тыс. руб. и более, в генеральной совокупности будет составлять от 15% до 45%.
Задание 4
Имеются следующие данные по двум организациям:
Таблица 10.
| Организация | Базисный период | Отчетный период | ||
| Средняя заработная плата, руб. | Среднесписочная численность работников, чел. | Средняя заработная плата, руб. | Фонд заработной платы, тыс. руб. | |
| №1 | 5000 | 100 | 6500 | 682,5 |
| №2 | 5600 | 100 | 8000 | 760,0 |
Определите:
1. Индексы динамики средней заработной платы по каждой организации.
2. По двум организациям вместе:
- индексы средней заработной платы переменного, постоянного состава и структурного сдвигов;
- абсолютное изменение средней заработной платы в целом и за счет отдельных факторов;
- абсолютное изменение фонда заработной платы вследствие изменения среднесписочной численности работников, средней заработной платы и двух факторов вместе.
Сделайте выводы.
Решение:
1. Индексы динамики средней заработной платы равны:
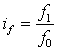
где f0 и f1 – заработная плата соответственно в базисном и отчетном периодах.
№1:
![]()
№2:
![]()
Таким образом, в отчетном периоде по сравнению с базисным периодом средняя заработная плата в организации №1 увеличилась на 30%, а во второй организации – на 42,8%.
2. Для дальнейших расчетов составим расчетную таблицу:
Таблица 11.
| Организация | Базисный период | Отчетный период | ||||||
| Средняя заработная плата, руб. | Среднесписочная численность работников, чел. | Фонд заработной платы, руб. | Средняя заработная плата, руб. | Фонд заработной платы, руб. | Среднесписочная численность работников, чел. | |||
| f0 | T0 | f0T0 | f1 | f1T1 | T1 | f0T1 | ||
| №1 | 5000 | 100 | 500000 | 6500 | 682500 | 105 | 525000 | |
| №2 | 5600 | 100 | 560000 | 8000 | 760000 | 95 | 532000 | |
| Итого | - | 200 | 1060000 | - | 1442500 | 200 | 1057000 | |
а) Индекс средней заработной платы переменного состава равен:
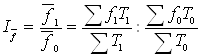
![]()
Абсолютное изменение средней заработной платы составило:
Df = 7212,5 – 5300 = 1912,5 (руб.)
б) Индекс средней заработной платы постоянного состава равен:
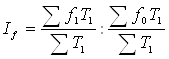
![]()
Абсолютное изменение средней заработной платы за счет изменения заработной платы по каждой организации отдельно составило:
Df(f) = 7212,5 – 5285 = 1927,5 (руб.)
в) Индекс структурных сдвигов равен:
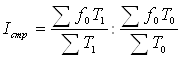
![]()
Абсолютное изменение средней заработной платы за счет структурных сдвигов в численности работников составило:
Df(стр.) = 5285 – 5300 = -15 (руб.)
Между вычисленными показателями существует следующая взаимосвязь:
![]()
1,361 = 1,365 * 0,997
Df = Df(f) + Df(стр.)
1912,5 = 1927,5 + (-15)
Таким образом, в отчетном периоде по сравнению с базисным средняя заработная плата по двум организациям увеличилась на 36,1% или на 1912,5 рублей. Это произошло под влиянием двух факторов. Во-первых, за счет увеличения заработной платы в каждой организации в отдельности средняя заработная плата по двум организациям вместе увеличилась на 36,5% или на 1927,5 руб. Во-вторых, за счет структурных изменений в численности работников (увеличения доли работников в организации с меньшей заработной платой) средняя заработная плата по двум организациям сократилась на 0,3% или на 15 рублей.
Абсолютное изменение фонда заработной платы за счет отдельных факторов определим, исходя из следующей модели:
IF = IT ´If
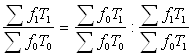
Итак, абсолютное изменение фонда заработной платы составило:
- вследствие изменения среднесписочной численности работников:
DF(T) = åf0T1 - åf0T0 = 1057000 – 1060000 = -3000 (руб.)
- вследствие изменения средней заработной платы:
DF(f) = åf1T1 - åf0T1 = 1442500 – 1057000 = 385500 (руб.)
- за счет двух факторов вместе:
DF = åf1T1 - åf0T0 = 1442500 – 1060000 = 382500 (руб.)
DF = DF(T) + DF(f)
382500 = -3000 + 385500
Таким образом, в отчетном периоде по сравнению с базисным фонд заработной платы по двум организациям в целом увеличился на 382500 руб. Это произошло под влиянием двух факторов. Во-первых, за счет сокращения среднесписочной численности работников фонд заработной платы сократился на 3000 руб. Во-вторых, за счет повышения средней заработной платы фонд заработной платы увеличился на 385500 руб.
Похожие работы
... труде наемного работника. Автор "Капитала" излагает свое представление о заработной плате, переходя от простого к сложному: от анализа сущности стоимости и цены рабочей силы к характеристике превращения стоимости и цены рабочей силы в заработную плату и особенностей ее форм - повременной и сдельной (поштучной). Так или иначе, на заработную плату влияют как продолжительность рабочего времени, ...
... пенсионные фонды, зачисляемые на личные счета работников, включаются наряду с другими материальными и социальными благами в денежном выражении в состав совокупного налогооблагаемого дохода работника. 1.5. Методика анализа фонда заработной платы Анализ фонда оплаты труда проводят по тому же плану, что и анализ других видов расходов: по сравнению с нормативной или плановой величиной либо ...
... план по договорным обязательствам, по объему перевозок, по номенклатуре грузов. Чем ближе значение показателя к 100%, тем ритмичнее работа автотранспортного предприятия, коэффициент ритмичности на рассматриваемом предприятии 100,46. 3. Статистическое изучение основного капитала По данным бухгалтерского учета стоимость основного капитала и его элементов известна по состоянию на начало и ...
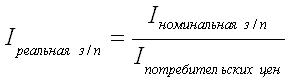
... так и реальной заработной плате Глава 2. Статистический анализ данных финансовой отчетности по оплате труда на ОАО «Бумажная Фабрика «Коммунар» В курсовой работе статистический анализ оплаты труда изучается на примере ОАО «Бумажная Фабрика «Коммунар». ОАО «Бумажная Фабрика «Коммунар» известный в России и за рубежом производитель упаковочных и технических видов бумаг и картона плотностью ...

0 комментариев