Навигация
Экономико-математическое моделирование
1. Графы
Задание 1.1
1. Охарактеризовать граф.
2. Выписать матрицу смежности графа.
3. Вычислить степени вершин.
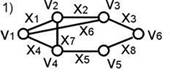
Решение:
Данный граф является неографом, так как его ребра не ориентированные и не имеют начало и конец.
Ст. V1 =3
Ст. V2 =3
Ст. V3 =3
Ст. V4 =3
Ст. V5 =2
Ст. V6 =2
Матрица смежности графа
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | |
| V1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| V2 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| V3 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| V4 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| V5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| V6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Задание 1.2
1. По матрице инцидентности нарисовать граф.
2. Охарактеризовать граф.
3. Назвать специальные вершины графа.
4. Вычислить полустепени вершин.
5. Выписать цикл, цепь, простой цикл, простую цепь.
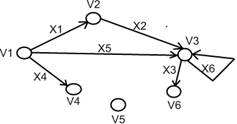
Решение:
Данный граф называется орграфом, так как его ребра ориентированы и имеют начало и конец.
V4 и V6 – висячие вершины;
V5 – изолированная вершина.
Полустепень захода: V2 = 1; V3 = 3; V4 = 1; V6 = 1.
Полустепень исхода: V1 = 3; V2 = 1; V3 = 2.
Цепь:
Х1 ![]() Х2
Х2 ![]() Х6
Х6 ![]() Х3
Х3
Х5 ![]() Х6
Х6 ![]() Х3
Х3
Простая цепь:
Х1 ![]() Х2
Х2 ![]() Х3
Х3
Х5 ![]() Х3
Х3
Цикл: ????
V3 ![]() V3
V3
Простой цикл: ????
V3 ![]() V3
V3
Задание 1.3
1. Нагрузить граф задания 1.1. согласно матрице длин дуг и нарисовать.
2. По алгоритму окрашивания найти кратчайший путь между вершинами V1 и V6.
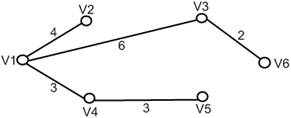
3. Построить покрывающее дерево с корнем в вершине V1.
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | |
| V1 |
| 4 | 6 | 3 |
|
|
| V2 | 4 |
| 3 | 2 |
|
|
| V3 | 6 | 3 |
|
|
| 2 |
| V4 | 3 | 2 |
|
| 3 |
|
| V5 |
|
|
| 3 |
| 2 |
| V6 |
|
| 2 |
| 0 |
|
Решение:
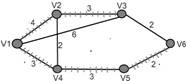
Окрасила вершину V1. d(V1) = 0, d(x) = ![]() для любого x
для любого x ![]() V1 и x = V1.
V1 и x = V1.
1. d (V2) = 4
d (V3) = 6
d (V4) = 3 – наименьшее; закрашиваю вершину V4 и дугу (V1, V4) или (V4, V2)
y = V4
2. d (V2) = 4 – наименьшее; закрашиваю вершину V2 и дугу (V1, V2)
d (V3) = 6
d (V5) = min (6; 3+3) = 6
d (V6) = ![]()
y = V2
3. d (V3) = 6 – наименьшее; закрашиваю вершину V3 и дугу (V2, V3)
d (V5) = 6
d (V6) = ![]()
y = V3
4. d (V5) = 6 – наименьшее; закрашиваю вершину V5 и дугу (V4, V5)
d (V6) = min (8; 6+2) = 8
y = V5
5. d (V6) = 8 – закрашиваю вершину V6 и дугу (V5, V6)
Кратчайший путь
V1 ![]() V3
V3 ![]() V6.
V6.
Покрывающее дерево:
Похожие работы
... отрезка времени. Как правило, это задача, решение которой влечет за собой постановки близких или аналогичных задач. Глава 2. Экономико-математическое моделирования процессов принятия управленческих решений. В классификации решений по времени действия выражается принцип их цикличности, определенная хронологическая последовательность, временные рамки которой неизбежно должны учитываться в процессе ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... <= 2,10 В разделе 1 проекта требуется: 1. Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Нужно формулировать экономико-математическую модель общей задачи линейного программирования (ОЗЛП); 2. С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы ...
0 комментариев