Вычислить временные параметры сетевой модели

2. Вычислить временные параметры сетевой модели.

3. Построить критический путь, вычислить критическое время, нанести критический путь на сетевой график.

Решение:

 

t_ij– время выполнения работ;

T_p– ранний срок наступления события;

K – номер вершины, при движении из которой было получено значение T_p;

T_п – поздний срок наступления события;

R_ij – полный резерв времени;

r_ij – свободный резерв времени.

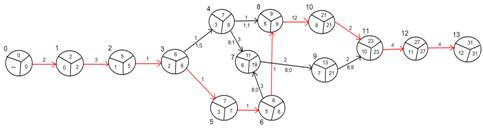
- критический путь.

Резервы нашла по формуле:

R_ij =  - T_i - t_ij

r_ij =  -  - t_ij

На критическом пути резервов времени нет.

 

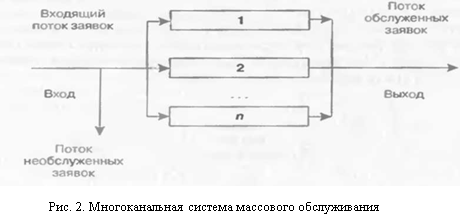
3. Система массового обслуживания (СМО)

 

Задание 3.1

 

Решить задачу для СМО с отказами:

В вычислительный центр с m ЭВМ поступают заказы на вычислительные работы. Если работают все m ЭВМ, то вновь поступающий заказ не принимается. Пусть среднее время работы с одним заказом составляет  часов. Интенсивность потока заявок равна λ (1/ч). Найти вероятность отказа Р_отк и m₃ – среднее число занятых ЭВМ.

 

m	3
λ	0,25
Тобсср	3

 

Решение:

Интенсивность потока обслуживаний  =  =  = 0,33. Интенсивность нагрузки ЭВМ по формуле

р = ; р =  = 0,75.

Предельные вероятности состояний:

р₀ = (1 + р +  + … +  + … + )^-1; р₀ = (1 + 0,75 + 0,75²/ 2! + 0,75³ / 3!)^-1 = 0,476 (нет ни одной заявки);

р_к = р^к / k! * р₀; р₃ = (0,75³ / 3!) * 0,476 = 0,033 (заняты три ЭВМ).

Вероятность отказа (когда заняты три ЭВМ), таким образом, Р_отк = р₃ = 0,033.

Относительная пропускная способность центра: Q = 1 - Р_отк ; Q = 1 – 0,033 = 0,967, т. е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.

Абсолютная пропускная способность центра А = λ Q; А = 0,25 * 0,967 = 0,242, т. е. в один час в среднем обслуживается 0,242 заявки.

Среднее число занятых ЭВМ:  = А / ;  = 0,242 / 0,033 = 0,725, т. е. каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на 72,5 / 3 = 24,2%.

Задание 3.2

 

Решить задачу для СМО с ограниченной длиной очереди:

На автозаправочной станции установлены m колонок для выдачи бензина. Около станции находится площадка на L машин для их ожидания в очереди. На станцию прибывает в среднем λ машин в минуту. Среднее время заправки одной машины  мин. Требуется определить вероятность отказа Р_отк и среднюю длину очереди М_ож.

 

m	3
L	3
λ	2
	1

Решение:

 = 1 /  = 1 мин.

Нахожу:

р = λ /  = 2 / 1 = 2, р / m = 2 / 3, тогда

р₀ = [ +  * ]^-1 = [1 + 2 + 2² / 2! + 2³ / 3! + 2⁴ / 3*3! * ]^-1  0.122

Р_отк = P_m+L =  * p₀ = (p/m)^L * (p^m/m!)*p₀ = (2/3)³ * (2³/3!) * 0.122 = 0.048;

М_ож =  ⁱ = (0.122*2³/3!) * [2/3 + 2(2/3)² + 3*(2/3)³] = 0.35

Таким образом, Р_отк = 0,048, М_ож = 0,35 машины.

 

4. Игры

 

Задание 4.1

 

1. Решить игру в чистых стратегиях.

2. Выписать седловые точки.

3. Вычислить цену игры.

 

	В1	В2	В3	В4
А1	1	4	1	2
А2	0	5	0	3
А3	1	3	1	3

 

Решение:

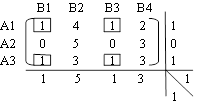
Седловые точки: (А1,В1); (А3,В1); (А1,В3); (А3,В3). V (цена игры) = 1.

Задание 4.2